Понятие, задачи и требования контрольной работы
Содержание
Введение. 3
Понятие, задачи и требования контрольной работы.. 4
Вопросы выносимые на контроль. Векторы и линейные операции над ними. 10
Демонстрационный вариант контрольной работы. 29
Заключение. 41
Список использованной литературы.. 42
Приложение к курсовой работе. 43
Введение
Контрольная работа это необходимая часть оценки усвоения знаний учащегося. Данный тип контроля применяется почти во всех учебных заведениях. Именно контрольные работы помогают выявить тот материал , которые не смогли усвоить студенты. При разработке контрольной работы преподавателю необходимо разработать такой комплекс упражнений, который смог бы охватить весь материал изученный студентами.
Цель курсовой работы : дать характеристику к разработке контрольной работе по алгебре на тему «Векторный метод в решении задач».
Задачи курсовой работы: раскрыть понятие контрольная работа, выявить недостатки и достоинства контрольной работы, раскрыть теоретические вопросы, выносимые на контроль на тему «Векторный метод в решении задач».
Объект исследования: требования к разработке контрольной работы и основные требования к ней.
Контрольные работы по алгебре особенно актуальны в учебных заведениях, так как в них четко видно, что студент усвоил, а что нет. При решении серии контрольных работ преподаватель может определить его уровень знаний по данной теме.
Можно сказать, что контрольные работы это хороший помощник для студентов заочного факультета. Преподаватель может предоставить им материал на самостоятельное изучение, а позже проверить, как студенты его освоили.
Конечно, к составлению измерительных работ необходимо подходить серьезно. Если составить случайный список заданий для контрольной работы, которые даже не встречались при изучении теории, то такая контрольная работа будет бесполезной, так как при решении такой работы студенты не смогут решить некоторые задания, что в свою очередь скажется на их оценке.
Таким образом к контрольной работе есть ряд требований и рекомендации об этом и пойдет речь в исследовательской работе.
Понятие, задачи и требования контрольной работы
Контрольная работа – один из основных видов самостоятельной работы студентов, представляющий собой изложение ответов на теоретические вопросы по содержанию учебной дисциплины и решение практических заданий.
Обычно проходит в письменном виде и на занятие и этим отличается от домашней работы. В ходе контрольной работы учащийся обычно не имеют права пользоваться учебниками, тетрадями, конспектами и т. п. После серии контрольных работ и ответов на уроке, в конце учебного года или по семестрам назначается экзамен и зачёт.
Такой тип контроля усвояемости знаний применяется как в высших учебных заведениях, так и в школах и на подготовительных курсах.
Также необходимо отметить, что контрольная работа – это основной способ поверки знаний студентов-заочников, поэтому они наиболее распространены на заочных факультетах.
В качестве целей контрольной работы можно выделить следующие:
· Развитие способности к углубленному анализу учебной и научной литературы, законодательства;
· Выработка умения систематизировать и обобщать научный и практический материал, критически его оценивать;
· Формирование и укрепление навыков овладения системой понятий данной науки, аргументированного, логичного, грамотного изложения ее выводов с использованием положений других наук;
· Развитие умения применять теоретические разработки для анализа, оценки, выявления и использования положительного опыта относительно темы контрольной работы;
Контрольные работы выполняются каждым студентом заочной формы обучения в соответствии с учебным планом; количество контрольных работ и дисциплины, по которым они выполняются, определяются учебным планом.
Выполнение студентом контрольной работы – составная часть учебного процесса, одна из форм организации и контроля самостоятельной работы студента.
Задачами выполнения контрольной работы являются:
· Самостоятельное изучение соответствующей темы (раздела) учебной дисциплины;
· Выявление способности решать задачи по изучаемой дисциплине.
· Контроль качества усвоения изученного материала и самостоятельной работы студента.
Задания для выполнения контрольных работ составляются преподавателем, проводящим занятия по соответствующей дисциплине, и доводятся до учащихся .
В современной дидактике понятие «контроль», (как, впрочем, и многие другие), не имеет однозначной трактовки. В одних источниках контроль определяют с точки зрения внешней структурной организации процесса обучения, в других – как часть процесса обучения. Некоторые исследователи вкладывают иной смысл в термин «контроль», приписывая ему значение «проверка»… Однако, сколько бы определений контроля не встречалось в работах дидактов, все они сводятся к общей сути: контроль - это соотнесение полученных результатов с поставленной целью. О степени достижения целей обучения судят по результатам обучения. Следовательно, для того чтобы определить при контроле, соответствуют ли подобные действия запланированным целям, необходимо эти цели выразить в категориях действий. Подобные результаты выступают как конкретизация целей обучения и являются не чем иным, как конкретными требованиями к усвоению, выраженными в определенных показателях – желаемых действиях учащихся. В отличие от реально достигнутых результатов их можно назвать необходимыми результатами усвоения (НРУ). НРУ выступают в этом случае как показатель (критерий) обученности.
Только после того, как будут определены конкретные требования к усвоению - НРУ соответствующего учебного материала, - можно приступать к подбору адекватных выявляемым результатам средств контроля – заданий, которые должны помочь установить наличие или отсутствие этих требований в достижениях учащихся. Тогда полученные результаты можно будет сопоставить с НРУ (показателями обученности), а выводы использовать для совершенствования следующего цикла процесса обучения.
Таким образом, проблема контроля состоит в нахождении объективного пути соотнесения достигнутых учащимися результатов с запланированными результатами обучения.
Решение задач контроля диктует следующие 4 принципа:
1. Принцип цели – определение цели контроля.
Формулировка цели контроля должна быть ориентирована на то содержание учебного курса или те или иные его аспекты, усвоение которых будет контролироваться.
2.Принцип объективности вывода результатов – установление конкретных объективно необходимых результатов обучения.
При контроле результатов усвоения учащимися того или иного материала должно предусматриваться по-возможности не только выявление этих результатов, но и их диагностика, т.е установление причин ошибок и пробелов в знаниях учащихся.
НРУ могут различаться по сложности в зависимости от состава умения. В зависимости от цели контроля тот или иной итог обучения может выступать как самостоятельное НРУ, так и в качестве показателя более комплексного НРУ.
Рассмотрим на конкретном примере. В качестве НРУ может выступать усвоение определенного понятия (вектор, скалярное произведение и т.д). При этом показателями данного результата могут стать умения:
· Воспроизвести определение понятия
· Конкретизировать ответ собственными примерами
· Подвести объект под понятие
· Выразить понятие в символической форме и т.д.
· В зависимости от целей контроля каждый из них может выступать как НРУ.
3.Принцип организации – организация контроля.
По мере изучения учебного материала идет углубление и расширение знаний. Поэтому при определении НРУ следует принимать во внимание место контроля. В зависимости от места контроля различают следующие его виды.
· По месту в учебном процессе:
- Вводный – актуализация опорных или остаточных знаний по теме
-Текущий – контроль усвоения учебного материала в самом ходе познавательного процесса
-Тематический – итоговый по теме (или другой логически завершенной части учебного материала
-Итоговый - контроль усвоения учебного материала за весь курс обучения
· По форме
-Индивидуальный
-Фронтальный (массовый)
· По способу
-Устный
-Письменный
-Практический
4.Принцип объективности оценки результатов – нахождение пути объективного анализа и оценки итогов контроля.
Анализ и оценка итогов контроля подразумевают сопоставление свойств (качеств) достигнутых учащимися результатов с запланированными НРУ. Для этой цели удобно использовать поэлементный анализ работы. Все основные принципы контроля должны быть отражены в общей задаче контроля. Только после этого можно приступить к подбору и конструированию соответствующих средств контроля.
Под термином «средство контроля знаний» следует понимать задание или несколько заданий (контрольная работа), предназначенных для осуществления определенных действий, направленных на выявление соответствующих результатов обучения (или отдельных показателей результатов). К средствам контроля в более широком смысле можно отнести все то, что способствует выявлению того или иного результата обучения. Содержание контрольных заданий должно определяться содержанием НРУ, для выявления которых они предназначены.
Классификация и типизация средств контроля:
· Контрольная работа (предполагает наличие заданий свободного ответа)
· Тест (предполагает задания с выбором предложенного ответа)
Использование любого средства контроля должно соответствовать целям контроля и отвечать следующим принципам.
Выделяют шесть принципов отбора и конструирования контрольных заданий:
1. Соответствие содержания задания контролируемому результату – адекватность содержанию и целям учебного курса.
2. Достоверность выявляемых заданием результатов – правильность, с которой задание выявляет то, что оно должно выявить.
3. Однозначность понимания всеми учащимися задания – четкое и однозначное отображение в формулировке желаемого результата.
4. Извлечение с помощью задания максимума информации об объекте контроля.
5. Увеличение числа выявляемых показателей при одновременном уменьшении времени контроля.
6. Составление инструкции, позволяющей однозначно оценить ответ учащегося на задание.
Таким образом, под контрольной работой понимается совокупность действий по решению заданий, с целью проверки полученных знаний в процессе обучения. Контрольная работа – это промежуточный этап контроля за обучаемыми с целью выявления уровня остаточных знаний. Для учащихся контрольная работа – это хорошая возможность проверить и закрепить свои знания практикой. Контрольные работы, как способ контроля, стоят на вооружении большинства учебных заведений.
Вопросы выносимые на контроль. Векторы и линейные операции над ними.
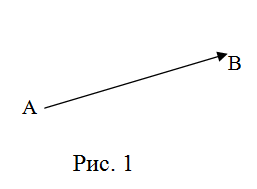
Определение. Вектором называется направленный отрезок (рис. 1).
А – начало, В – конец вектора 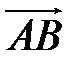 .
. 
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение. Вектором называется упорядоченная пара точек.
Определение. Длина вектора 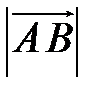 – расстояние между его началом и концом.
– расстояние между его началом и концом.
Определение. Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
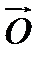 – нулевой вектор: его направление не определено, а длина
– нулевой вектор: его направление не определено, а длина 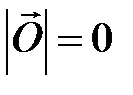 .
.
Определение. Векторы 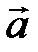 и
и 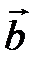 называются коллинеарными, если они лежат на параллельных прямых:
называются коллинеарными, если они лежат на параллельных прямых: 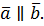
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение. Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
а) Правило параллелограмма (рис.2): начала 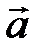 и и 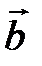 совмещаются в одной точке, и совмещаются в одной точке, и 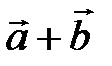 – диагональ параллелограмма, построенного на – диагональ параллелограмма, построенного на 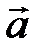 и и 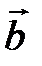 . . | б) Правило треугольника (рис. 3): начало 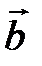 совмещается с концом совмещается с концом 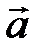 , и , и 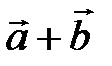 направлен от начала направлен от начала 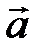 к концу к концу 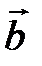 . . | ||||||||||
Рис. 2 |
Рис. 3 |
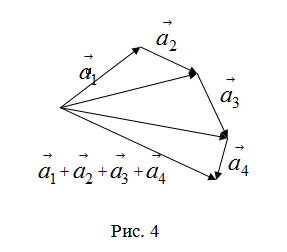 в) Правило сложения нескольких векторов (рис. 4).
в) Правило сложения нескольких векторов (рис. 4).
Вектор 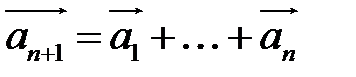 замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и 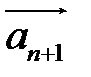 направлен от начала направлен от начала 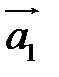 к концу к концу 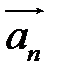 . . |
Умножение на число
Определение. Произведением вектора 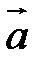 на число
на число 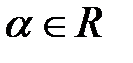 называется вектор
называется вектор 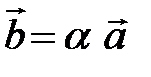 , удовлетворяющий условиям:
, удовлетворяющий условиям:
а) 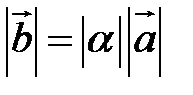 ;
;
б) 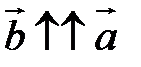 , если
, если 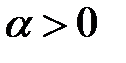 ,
, 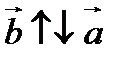 , если
, если 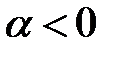 и
и 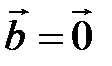 , если
, если 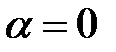 .
.
Произведение 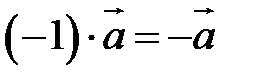 называется вектором, противоположным вектору
называется вектором, противоположным вектору 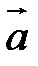 . Очевидно,
. Очевидно, 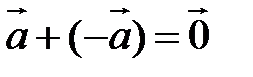 .
.
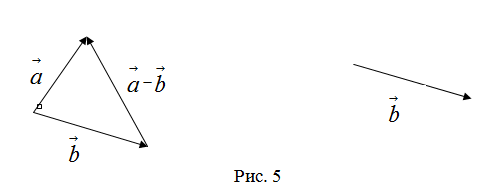 Определение. Разностью
Определение. Разностью 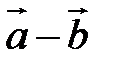 называется сумма вектора
называется сумма вектора 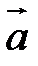 и вектора, противоположного
и вектора, противоположного 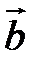 :
: 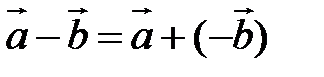 (рис. 5).
(рис. 5).
Начала  и
и  совмещаются в одной точке, и
совмещаются в одной точке, и  направлен от конца
направлен от конца 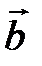 к концу
к концу 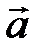 .
.
Свойства линейных операций.
1. 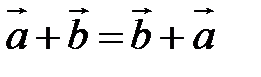 | 2. 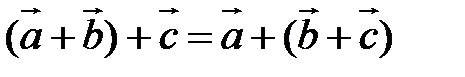 |
3. 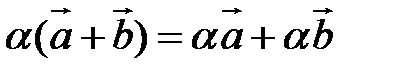 | 4. 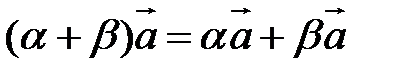 |
5. 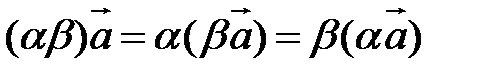 |
Определение. Результат конечного числа линейных операций над векторами называется их линейной комбинацией: 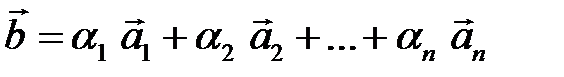 ,
, 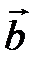 – линейная комбинация векторов
– линейная комбинация векторов 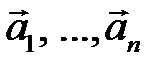 с коэффициентами
с коэффициентами 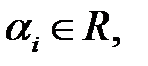
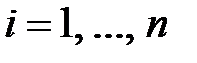 .
.
| Рис.6 |
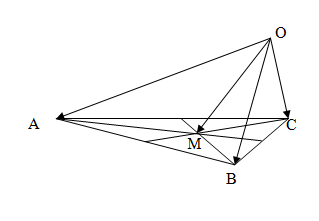 Пример.Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить
Пример.Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 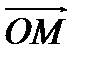 как линейную комбинацию
как линейную комбинацию 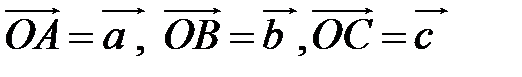 (рис. 6).
(рис. 6).
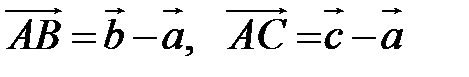 . Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что
. Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что 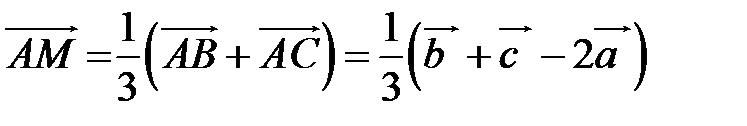 .
.
По правилу треугольника 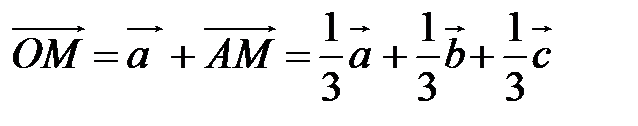 , то есть
, то есть 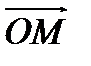 – линейная комбинация
– линейная комбинация  с коэффициентами
с коэффициентами 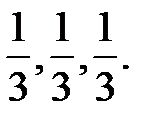
Теорема 1. Пусть 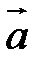 и
и 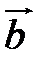 – неколлинеарные векторы. Тогда любой компланарный с ними вектор
– неколлинеарные векторы. Тогда любой компланарный с ними вектор 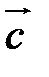 может быть представлен в виде
может быть представлен в виде
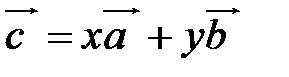 ,
, 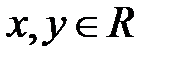 , (2.1) где коэффициенты (2.1) определяются единственным образом.
, (2.1) где коэффициенты (2.1) определяются единственным образом.
Представление вектора 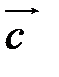 в виде (2.1) называется разложением его по двум неколлинеарным векторам.
в виде (2.1) называется разложением его по двум неколлинеарным векторам.
Теорема 2. Пусть 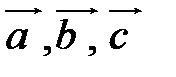 – некомпланарные векторы. Тогда любой вектор
– некомпланарные векторы. Тогда любой вектор 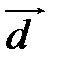 может быть представлен в виде
может быть представлен в виде
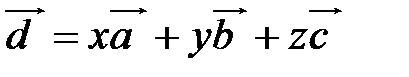 ,
, 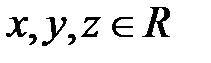 , (2.2) причем единственным образом.
, (2.2) причем единственным образом.
Представление вектора 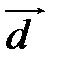 в виде (2.2) называется разложением его по трем некомпланарным.
в виде (2.2) называется разложением его по трем некомпланарным.
Проекция вектора на ось.
Координаты вектора.
Определение. Осью называется направленная прямая.
Определение. Ортом оси  называется единичный вектор
называется единичный вектор 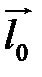 , направление которого совпадает с направлением оси.
, направление которого совпадает с направлением оси.
Определение. Ортогональной проекцией точки М на ось  называется основание М1 перпендикуляра, опущенного из М на
называется основание М1 перпендикуляра, опущенного из М на  .
.
Определение. Ортогональной проекцией вектора 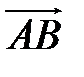 на ось
на ось  называется длина отрезка А1В1 этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора
называется длина отрезка А1В1 этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора 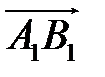 совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
| Рис.8 |
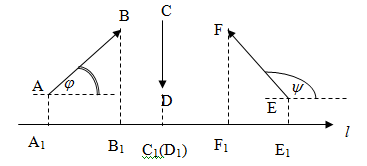
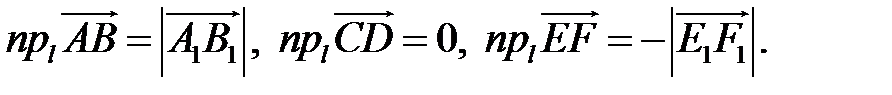
Определение. Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки). 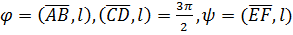 (рис. 8).
(рис. 8).

Очевидно, проекцию вектора на ось можно найти по формуле
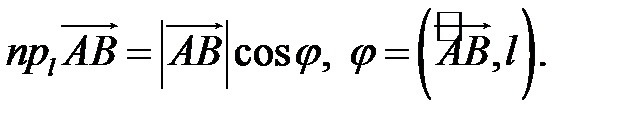
Можно показать, что проекция линейной комбинации векторов равна такой же линейной комбинации их проекций:
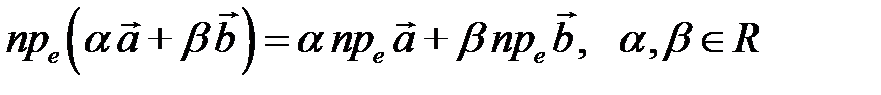 .
.
В частности, проекция суммы векторов равна сумме их проекций:
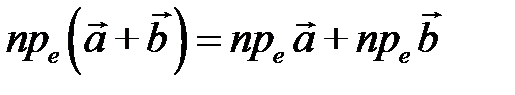 .
.
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 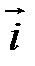 – орт оси ОХ,
– орт оси ОХ, 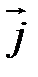 – орт оси OY. Выберем точку
– орт оси OY. Выберем точку  , и пусть
, и пусть 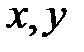 – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).
– проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).
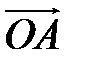 – радиус-вектор точки – радиус-вектор точки 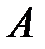 и и 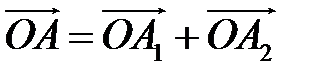 , но , но 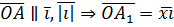 Аналогично Аналогично 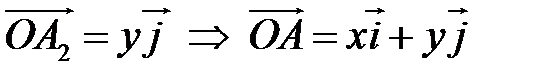 – разложение – разложение 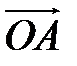 по ортам координатных осей по ортам координатных осей 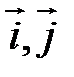 (разложение единственно по теореме 1). (разложение единственно по теореме 1). |
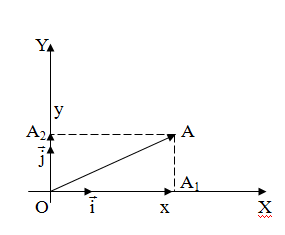
| Рис.9 |
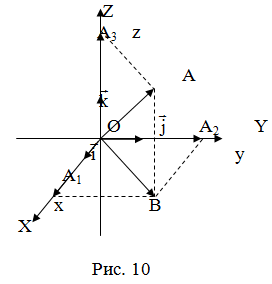
Аналогично в пространственной системе OXYZ 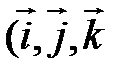 – орты координатных осей) (рис. 10):
– орты координатных осей) (рис. 10):
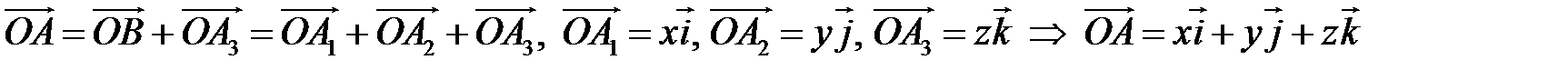 – разложение
– разложение 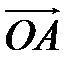 по ортам координатных осей (единственно по теореме 2).
по ортам координатных осей (единственно по теореме 2).
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 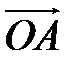 можно связать три числа
можно связать три числа 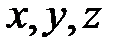 (или два числа
(или два числа 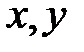 , если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
, если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
Определение. Координатами вектора 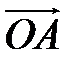 в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
Таким образом, можно дать еще одно определение вектора.
Определение. Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример. Если 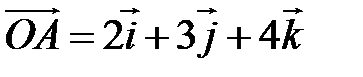 , то
, то 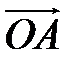 =(2,3,4) и наоборот, если
=(2,3,4) и наоборот, если 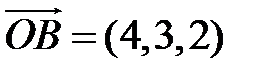 , то
, то 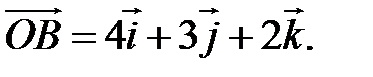
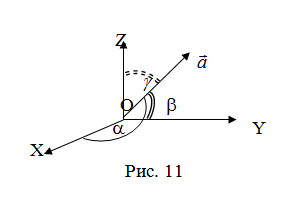
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
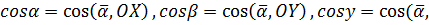 OZ).
OZ).
.
Из этих формул очевидно следует основное свойство направляющих косинусов: 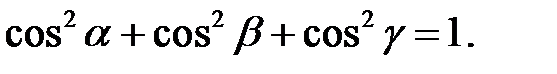 Если известны длина Если известны длина  и направляющие косинусы вектора, то его координаты вычисляются по формулам: и направляющие косинусы вектора, то его координаты вычисляются по формулам: |
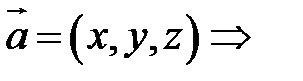
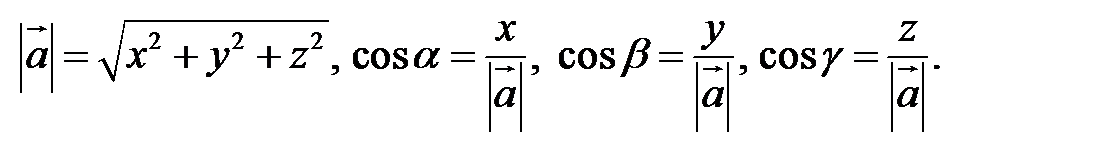
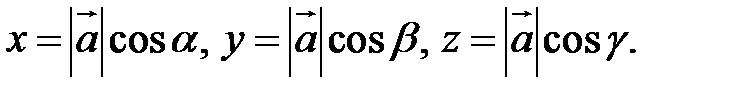
Пусть 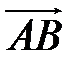 – произвольный вектор в системе OXYZ, – произвольный вектор в системе OXYZ, 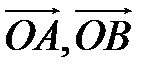 – радиус-векторы его начала и конца, – радиус-векторы его начала и конца, 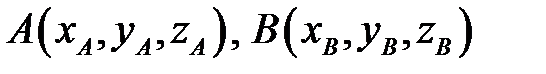 , (рис.12). Тогда: , (рис.12). Тогда: 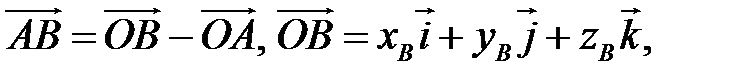 |
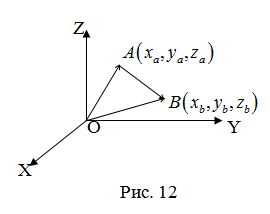
 (см. свойства линейных операций над векторами). Таким образом,
(см. свойства линейных операций над векторами). Таким образом,  , то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
, то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
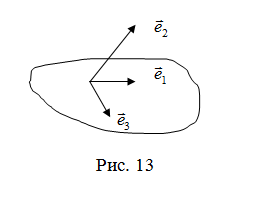 Определение. Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Определение. Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если 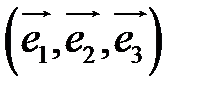 – базис, то
– базис, то 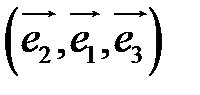 – другой базис, так как изменился порядок следования векторов.
– другой базис, так как изменился порядок следования векторов.
Определение. Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать 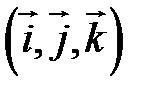 .
.
Из теоремы 2 следует, что всякий вектор 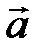 может быть разложен по базису
может быть разложен по базису 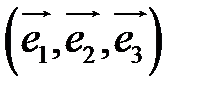 , то есть представлен в виде:
, то есть представлен в виде: 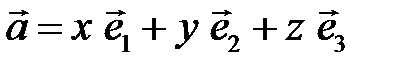 . Числа
. Числа 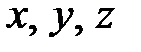 называются координатами
называются координатами 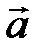 в базисе
в базисе 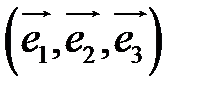 .
.
Определение. Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 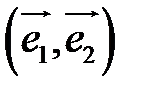 – базис, то представление вектора в виде
– базис, то представление вектора в виде 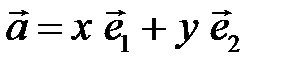 называется разложением
называется разложением 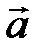 по базису
по базису 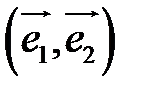 и
и 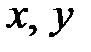 – координаты
– координаты 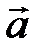 в этом базисе.
в этом базисе.
Определение. Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении.
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда 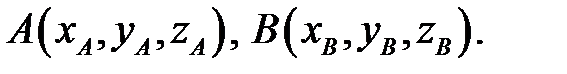 Обозначим Обозначим 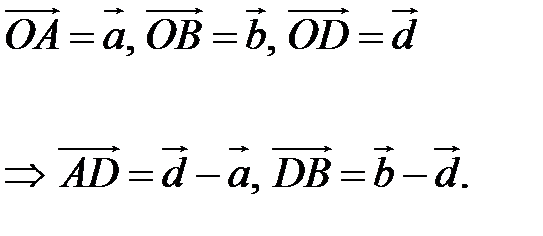 |
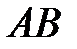 . Найти точку
. Найти точку 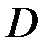 , которая делит
, которая делит 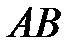 в заданном отношении
в заданном отношении 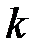 :
: 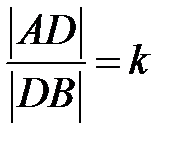 (рис. 14).
(рис. 14). 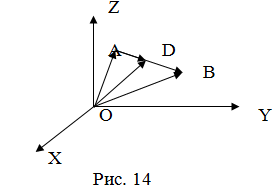
Так как 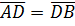 (лежат на одной прямой) и
(лежат на одной прямой) и 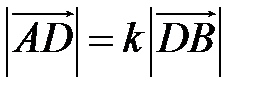 , то
, то 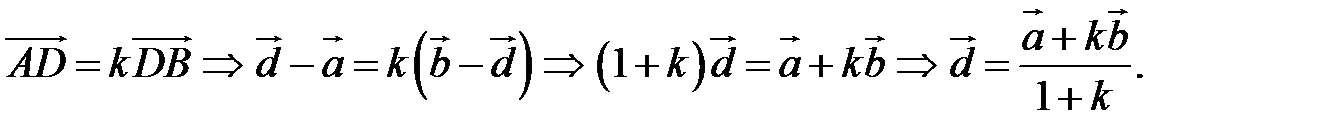 Переходя от этого векторного равенства к равенству соответствующих координат, получим:
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
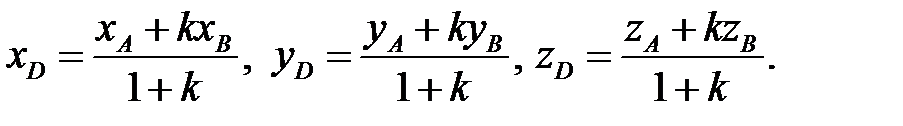 (2.3)
(2.3)
Замечание 1. Если 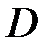 – середина отрезка
– середина отрезка 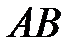 , то
, то 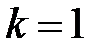 , поэтому
, поэтому
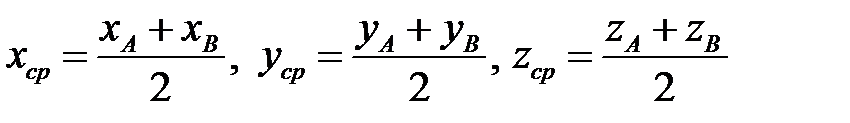 (2.4)
(2.4)
Замечание 1. Если 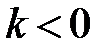 ,
, 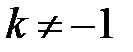 , то точка
, то точка 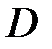 лежит за пределами
лежит за пределами 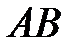 : так как
: так как 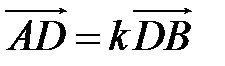 , то при
, то при 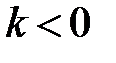
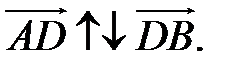
В этом случае 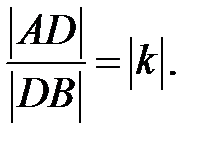 Пусть Пусть 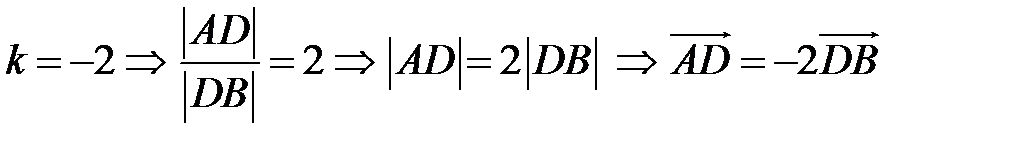 (рис. 15). (рис. 15). |
Скалярное произведение векторов
Определение. Скалярным произведением векторов 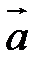 и
и 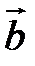 называется скаляр (число), равный
называется скаляр (число), равный 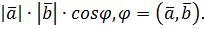
Скалярное произведение обозначается так: 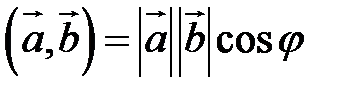 или
или 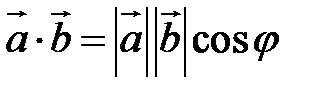 .
.
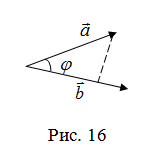 | Так как 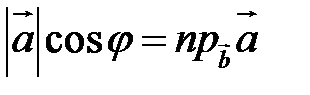 (рис. 16) или (рис. 16) или 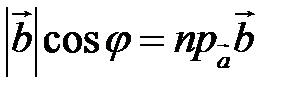 , то , то 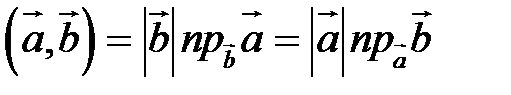 . . |
Свойства скалярного произведения
1. 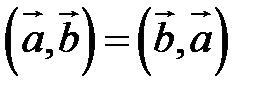 – очевидно из определения.
– очевидно из определения.
2. 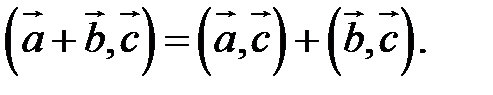
3. 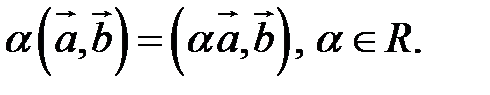
4. 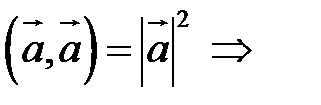
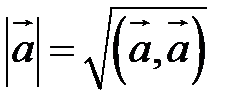 .
.
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5. 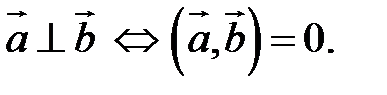
Пример. Найти, при каком значении 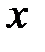 векторы
векторы 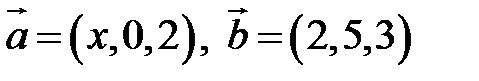 перпендикулярны.
перпендикулярны.
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5): 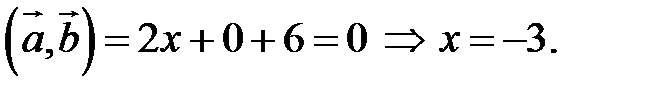
Пример. Найти угол между биссектрисой 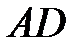 и медианой AM‖ABC, если
и медианой AM‖ABC, если 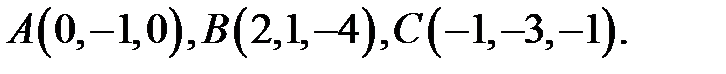
Так как 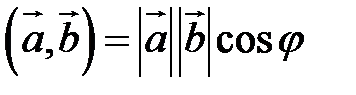 , то
, то 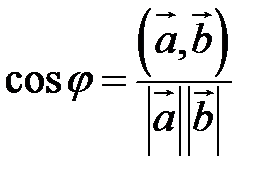 . (2.6)
. (2.6)
Найдем координаты векторов 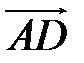 и
и 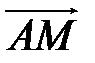 . Точка
. Точка 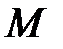 – середина
– середина 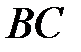 , поэтому по формулам (2.4)
, поэтому по формулам (2.4) 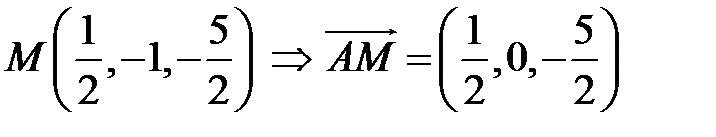 .
.
По теореме о биссектрисе внутреннего угла треугольника 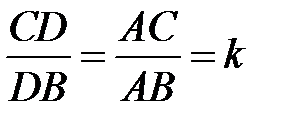 . Чтобы найти
. Чтобы найти 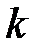 , вычислим длины
, вычислим длины 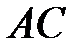 и
и 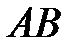 :
:
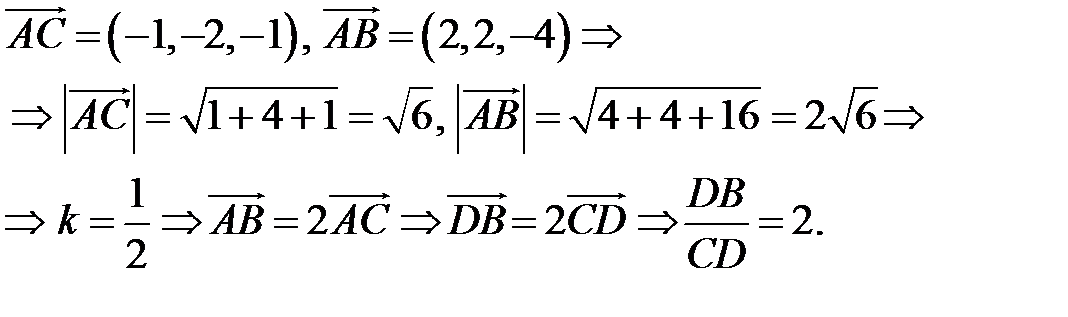
Разделим отрезок  в данном отношении по формулам (2.3):
в данном отношении по формулам (2.3):
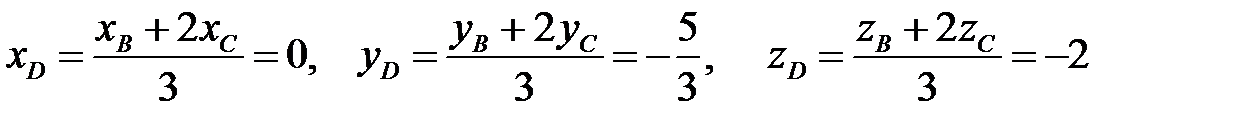 ,
,
отсюда 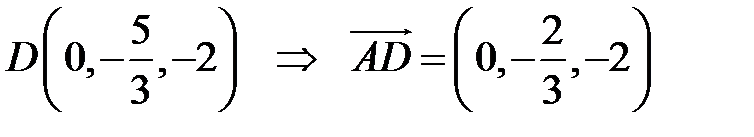 .
.
Заметим, что 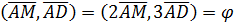 . Это замечание позволит нам не иметь дело с дробями, так как
. Это замечание позволит нам не иметь дело с дробями, так как
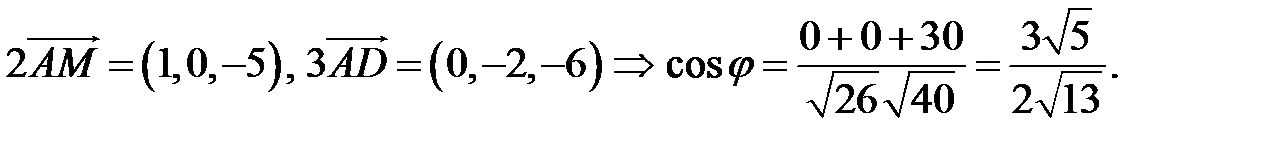
Пример. Найти 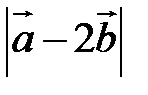 , если
, если 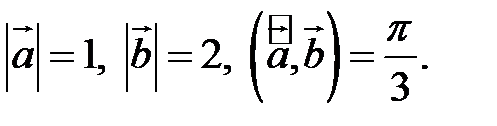
Воспользуемся свойствами 1–4 скалярного произведения:
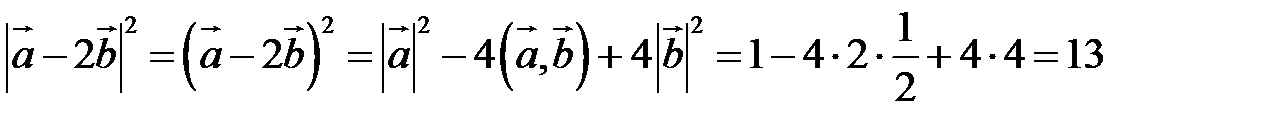 .
.
Отсюда 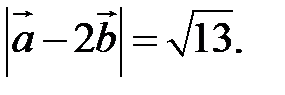
Замечание. Так как работа силы  по перемещению материальной точки вдоль вектора
по перемещению материальной точки вдоль вектора  вычисляется по формуле
вычисляется по формуле 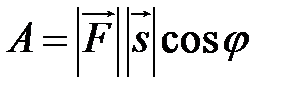 , то
, то 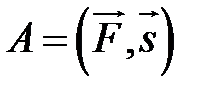 .
.
Векторное произведение векторов
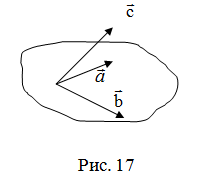
Определение. Тройка некомпланарных векторов 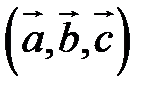 , имеющих общее начало, называется правой (левой), если с конца третьего вектора
, имеющих общее начало, называется правой (левой), если с конца третьего вектора 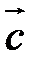 вращение первого вектора
вращение первого вектора 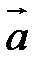 ко второму вектору
ко второму вектору 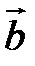 по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
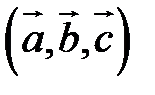 – левая тройка, – левая тройка, 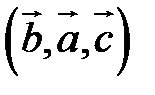 – правая тройка, – правая тройка, 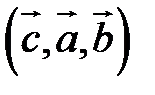 – левая тройка. – левая тройка. |
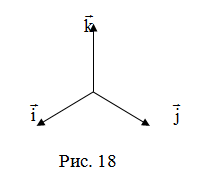
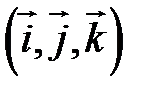 – правая тройка (рис. 18). – правая тройка (рис. 18). |
Определение. Векторным произведением вектора 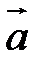 на вектор
на вектор 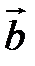 называется вектор
называется вектор 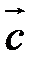 , удовлетворяющий условиям:
, удовлетворяющий условиям:
1. 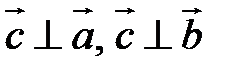 (
( 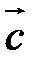 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 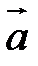 и
и 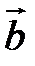 ).
).
2. Направление 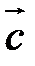 таково, что тройка
таково, что тройка 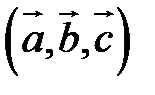 – правая.
– правая.
3. 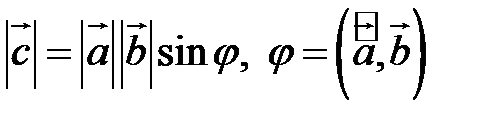 .
.
Векторное произведение обозначается так: 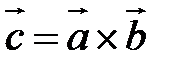 или
или 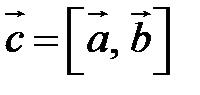 .
.
Замечание. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
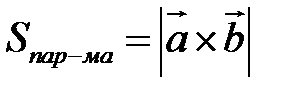 .
.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
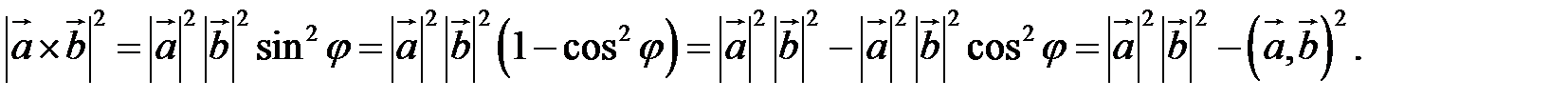
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
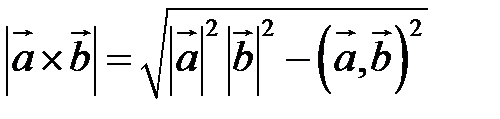 . (2.7)
. (2.7)
Пример. Найти площадь параллелограмма, построенного на векторах 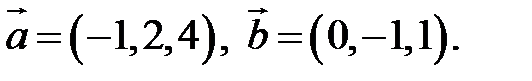
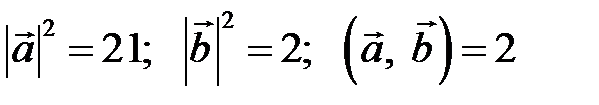 .
.
По формуле (2.7): 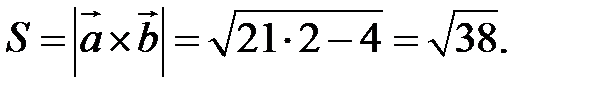
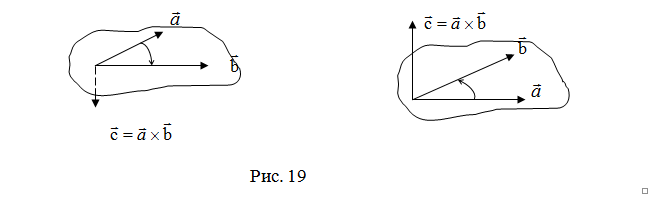
Замечание 2. Направление вектора  можно также (кроме п.2) определить по правилу винта: направление вектора
можно также (кроме п.2) определить по правилу винта: направление вектора  совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора
совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора 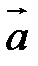 ко второму вектору
ко второму вектору 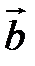 по кратчайшему пути (рис. 19).
по кратчайшему пути (рис. 19).
Свойства векторного произведения.
1. 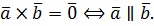
2. 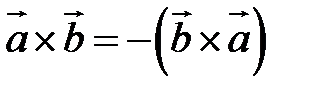 .
.
3. 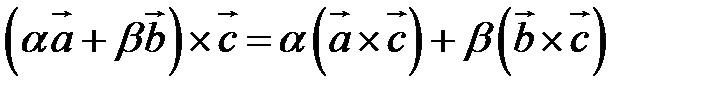 – свойство линейности векторного произведения по первому сомножителю (без доказательства).
– свойство линейности векторного произведения по первому сомножителю (без доказательства).
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов  : векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
: векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
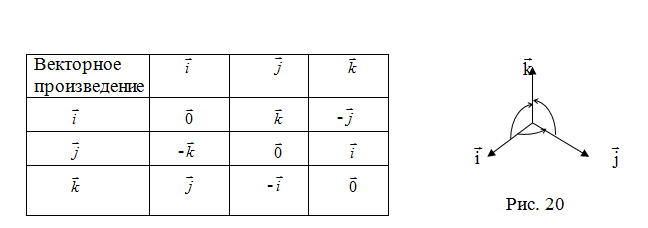
Пусть в некоторой пдск 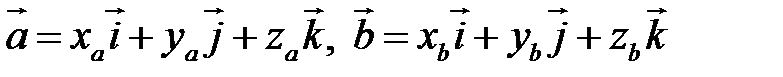 . Найдем векторное произведение этих векторов:
. Найдем векторное произведение этих векторов:
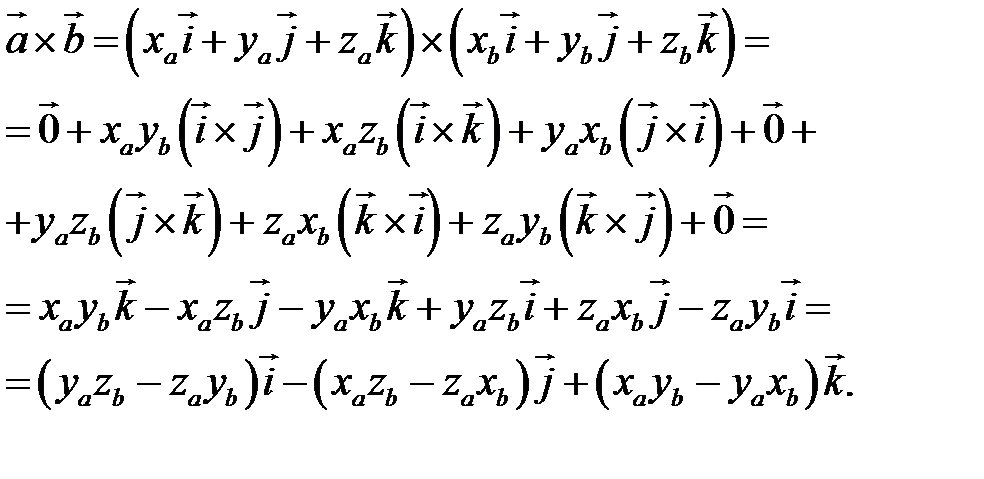
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
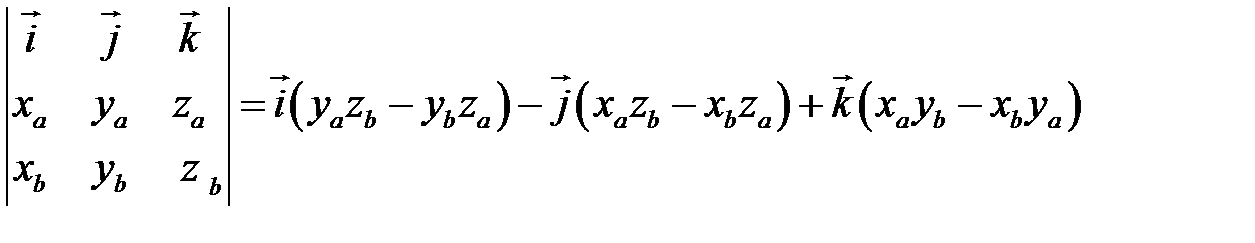 .
.
Таким образом,
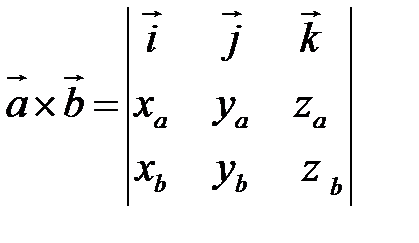 . (2.8)
. (2.8)
Пример. Вычислить векторное произведение векторов 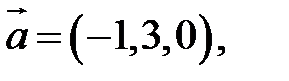
По формуле (2.8): 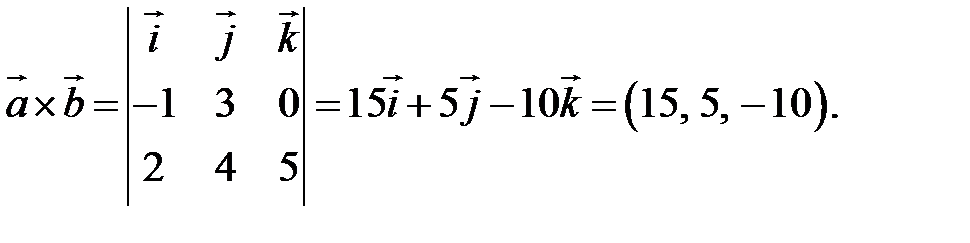
Заметим, что площадь треугольника, построенного на векторах  и
и 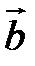 , можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что
, можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что 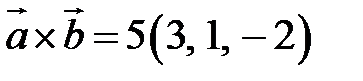 .
.
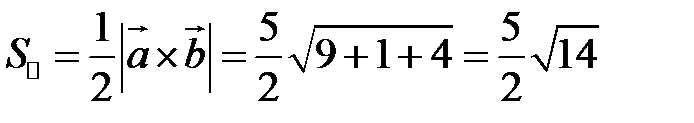
или
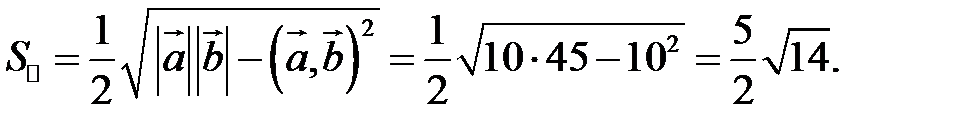
Пример. Вычислить площадь параллелограмма, построенного на векторах 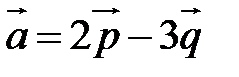 и
и 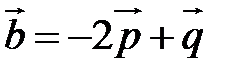 , если
, если 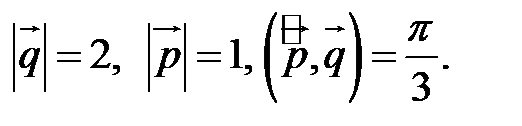
Так как 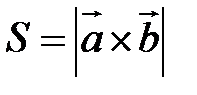 , то вычислим векторное произведение, используя его свойства:
, то вычислим векторное произведение, используя его свойства: 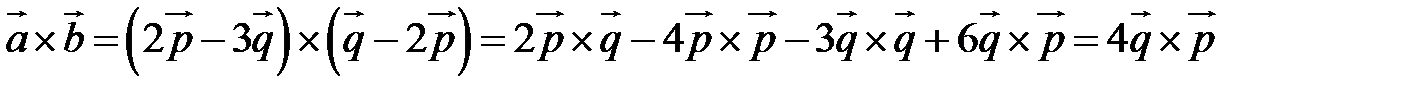 .
.
Отсюда 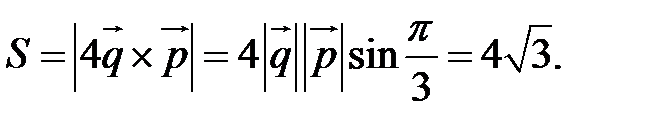
Смешанное произведение векторов
Определение. Смешанным произведением векторов 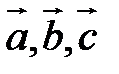 называется число
называется число 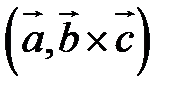 – скалярное произведение
– скалярное произведение 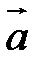 на векторное произведение
на векторное произведение 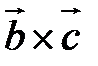 .
.
Смешанное произведение обозначается так: 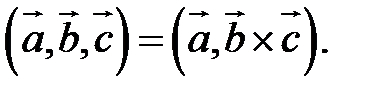
Пусть в некоторой пдск 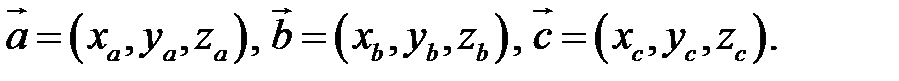
Обозначим
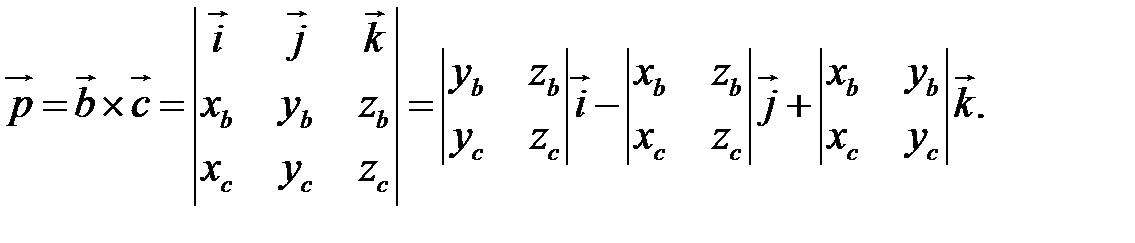
Тогда
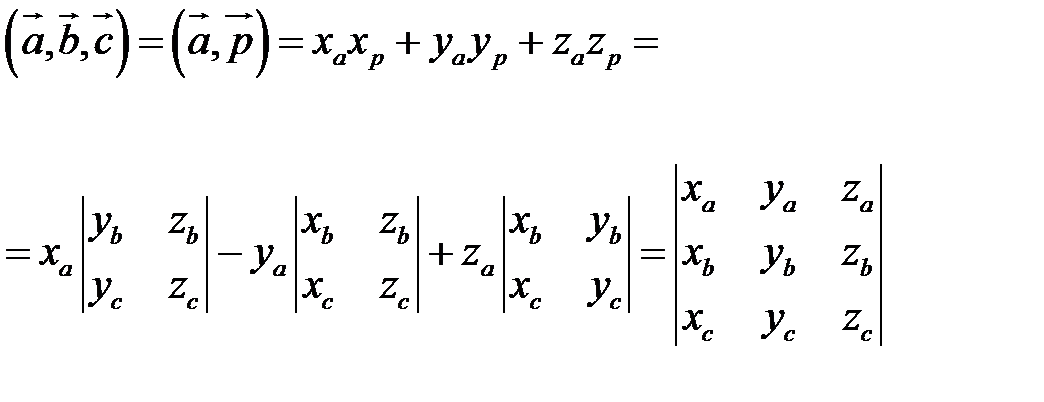
Таким образом,
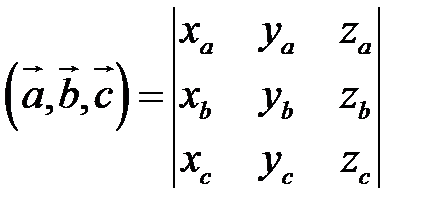 (2.9)
(2.9)
По определению скалярного произведения 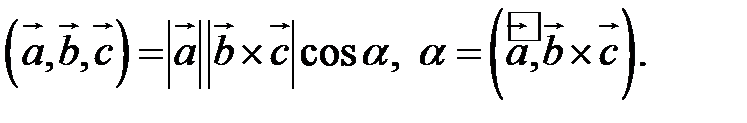 Совместим начала всех трех векторов в одной точке. Тогда (рис. 21) Совместим начала всех трех векторов в одной точке. Тогда (рис. 21) 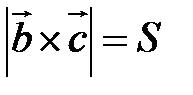 – площадь параллелограмма, – площадь параллелограмма, 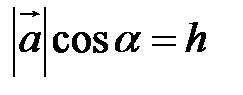 – высота параллелепипеда, – высота параллелепипеда, 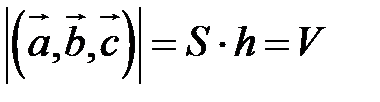 – объем параллелепипеда. – объем параллелепипеда. |
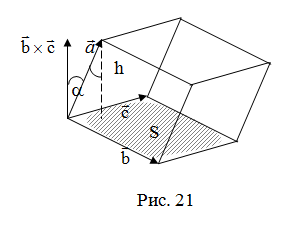
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 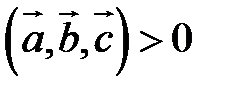 , если
, если  – правая тройка, и
– правая тройка, и 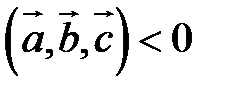 , если
, если  – левая тройка.
– левая тройка.
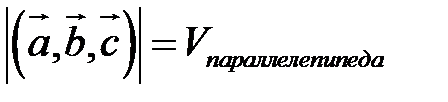 .
.
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 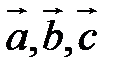 компланарны
компланарны 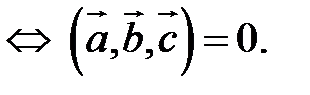
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
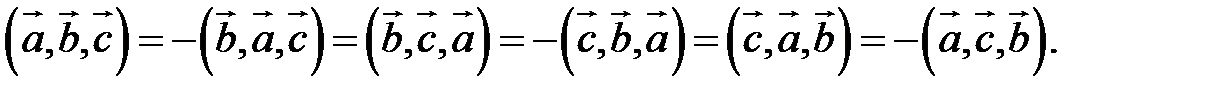
3. В смешанном произведении векторное и скалярное произведения можно менять местами: 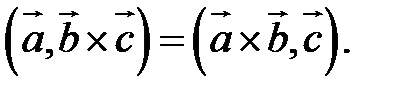
4. Смешанное произведение линейно по каждому из трех сомножителей.
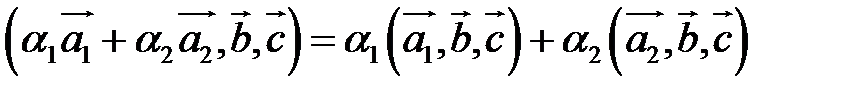 – линейность по первому сомножителю.
– линейность по первому сомножителю.
Пример. Найти объем тетраэдра, построенного на векторах 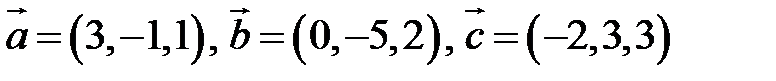 , и его высоту, перпендикулярную плоскости векторов
, и его высоту, перпендикулярную плоскости векторов  и
и 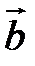 .
.
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому 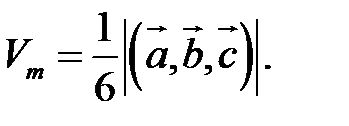
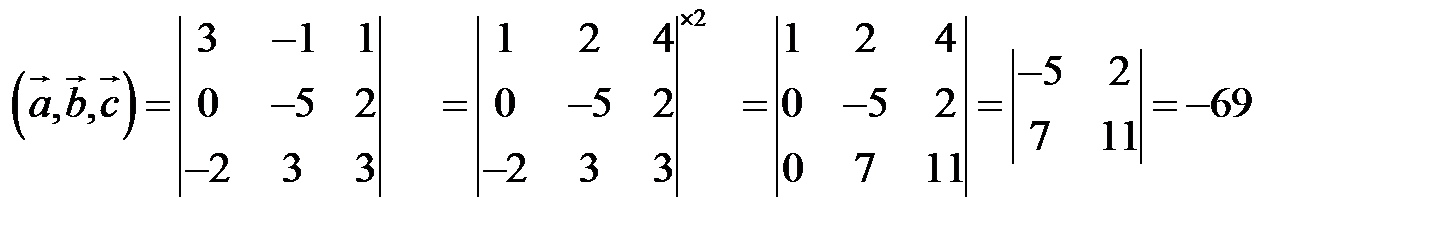 .
.
Отсюда 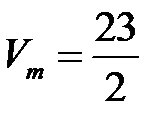 (заметим, что
(заметим, что 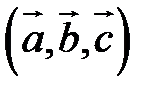 – левая тройка, так как смешанное произведение отрицательно).
– левая тройка, так как смешанное произведение отрицательно).
Чтобы найти высоту, воспользуемся формулой
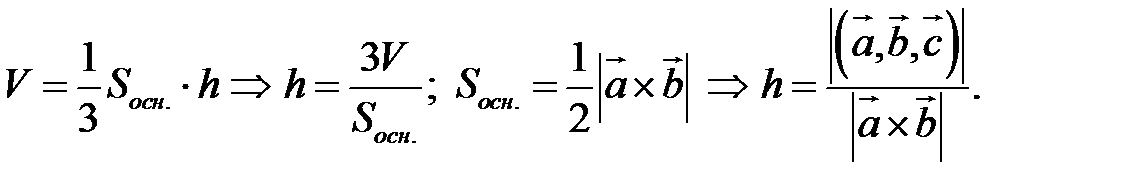
По формуле (2.7) 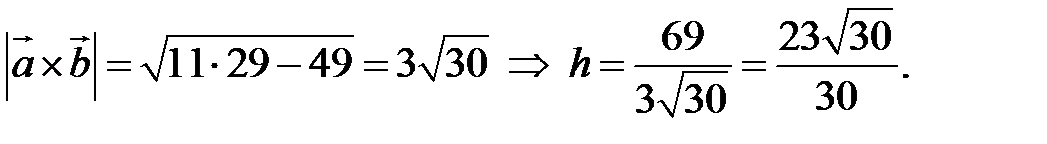
Демонстрационный вариант контрольной работы.
Задание №1. Даны координаты вершин пирамиды А1А2А3А4 : А1(1;2;1), А2(3;-1;7), А3(2;0;2), А4(7;4;-2).. Требуется найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды.
Решение:
1. Находим координаты вектора 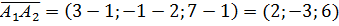 и длину ребра
и длину ребра 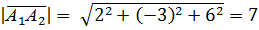
2. Угол 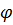 между ребрами А1А2 и А1А4 вычисляется по формуле
между ребрами А1А2 и А1А4 вычисляется по формуле
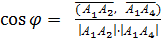 из скалярного произведения.
из скалярного произведения. 
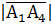 =
= 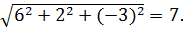
Поэтому:
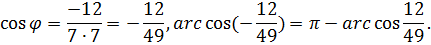
3. Угол  между ребром А1А4 и плоскостью А1А2А3 – это угол между вектором
между ребром А1А4 и плоскостью А1А2А3 – это угол между вектором  и его ортогональной проекцией А1А4` на грань А1А2А3.
и его ортогональной проекцией А1А4` на грань А1А2А3.
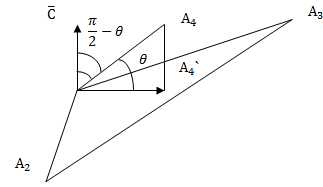
Вектор 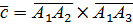 перпендикулярен грани А1А2А3, что вытекает из определения векторного произведения векторов
перпендикулярен грани А1А2А3, что вытекает из определения векторного произведения векторов 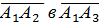 :
:
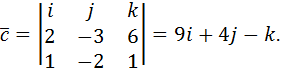 (Здесь
(Здесь 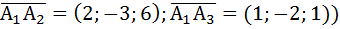 . Как и в предыдущем пункте , находим
. Как и в предыдущем пункте , находим
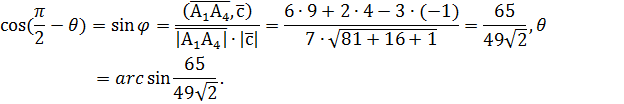
4. Площадь грани А1А2А3 находим, используя смысл векторного произведения:
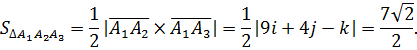
5.Объем пирамиды А1А2А3А4 численно равен одной шестой модуля смешанного произведения векторов 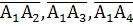 .
.
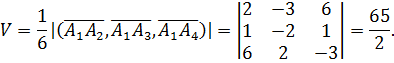
Задание №2.
В кубе АBCDA1B1C1D1 со стороной a точка К является серединой стороны основания В1С1, точка L делит другую сторону C1D1 этого основания в отношении 2:1, считая от вершины С1, точка N является серединой бокового ребра АА1. Найдите площадь сечения, проходящего через точки К, L,N.
Решение:
Построим сечение куба через точки K, L, N.
(A1B1C1) KL 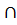 A1D1 = Q, (AA1D1) NQ
A1D1 = Q, (AA1D1) NQ 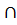 DD1=T, (BB1C) KG
DD1=T, (BB1C) KG 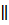 TN, NTLKG – искомое сечение. Площадь сечения вычислим, используя формулу
TN, NTLKG – искомое сечение. Площадь сечения вычислим, используя формулу 
 угол между нормальными векторами плоскости основания куба и плоскости сечения. Площадь проекции сечения куба на плоскость ABC можно вычислить как
угол между нормальными векторами плоскости основания куба и плоскости сечения. Площадь проекции сечения куба на плоскость ABC можно вычислить как 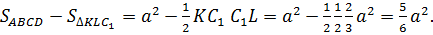 В декартовой системе координат с центром в вершине куба A координаты вершин имеют вид: K
В декартовой системе координат с центром в вершине куба A координаты вершин имеют вид: K 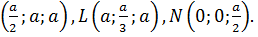 Отсюда
Отсюда 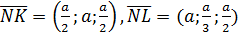 . Нормальный вектор
. Нормальный вектор 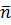 сечения можно принять пропорциональным (коллинеарным) векторному произведению
сечения можно принять пропорциональным (коллинеарным) векторному произведению 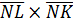 .
.
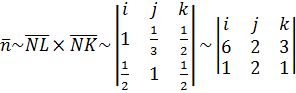 = (-4;-3;10). Нормальный вектор плоскости основания
= (-4;-3;10). Нормальный вектор плоскости основания 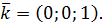 Тогда
Тогда 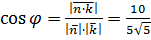 и
и 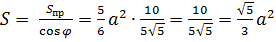
Ответ: 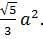
Задание №3.
Даны координаты вершин параллелепипеда: A(1;2;3), B(0;1;2), C(1;1;3), D(0;0;3). Найти объем параллелепипеда, его высоту, опущенную из вершины С, угол между вектором AD и гранью, в которой лежат векторы АВ и АС.
Решение: По определению, объем параллелепипеда равен смешанному произведению векторов, на которых он построен. Найдем эти векторы:
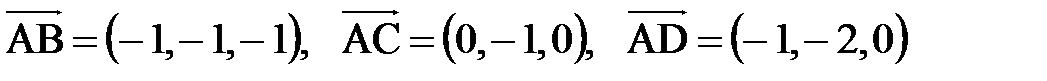 .
.
Объем этого параллелепипеда 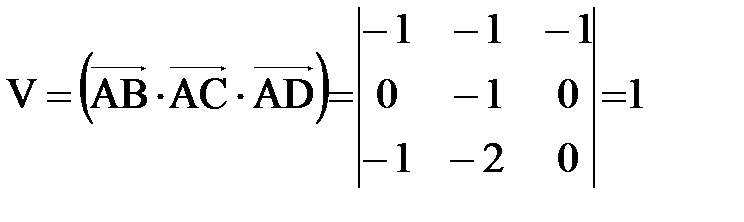 .
.
С другой стороны, объем параллелепипеда 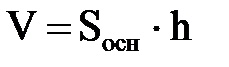 ,
, 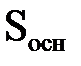 - это площадь параллелограмма:
- это площадь параллелограмма: 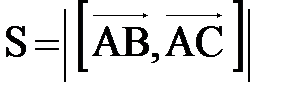 .
.
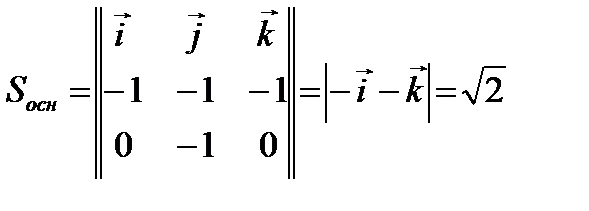 , тогда высота
, тогда высота 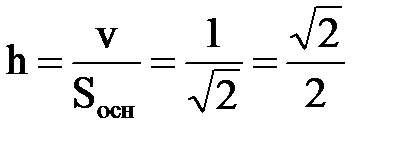 .
.
Угол между вектором и гранью 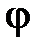 найдем по формуле
найдем по формуле
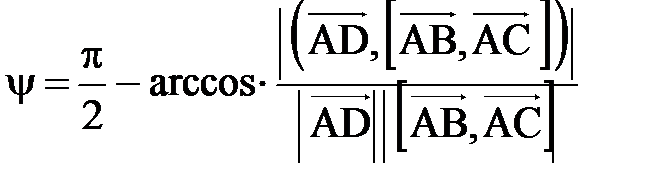 .
.
Так как вектор 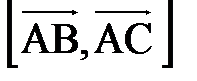 перпендикулярен грани, в которой лежат векторы
перпендикулярен грани, в которой лежат векторы 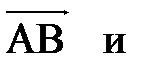
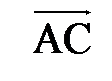 . Угол между этим вектором и вектором
. Угол между этим вектором и вектором 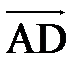 находим по известной формуле
находим по известной формуле
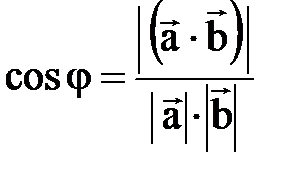 . Очевидно, что искомый угол
. Очевидно, что искомый угол 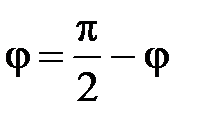 .
.
Итак: 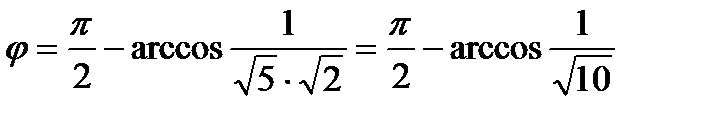 .
.
Задание №4.
Проверить, лежат ли в одной плоскости точки 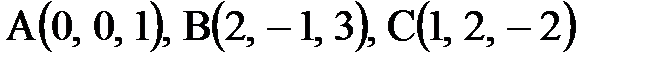 ,
, 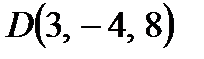 . Найти линейную зависимость вектора
. Найти линейную зависимость вектора 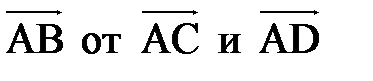 , если это возможно.
, если это возможно.
Решение: Найдем три вектора: 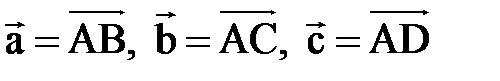 .
.
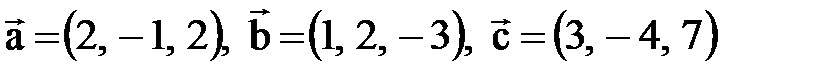 .
.
Три вектора лежат в одной плоскости, если они компланарны, т. е. их смешанное произведение равно нулю: 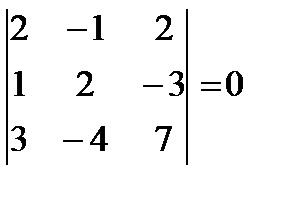 . Следовательно, эти три вектора линейно зависимы. Найдем линейную зависимость
. Следовательно, эти три вектора линейно зависимы. Найдем линейную зависимость 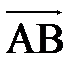 от
от 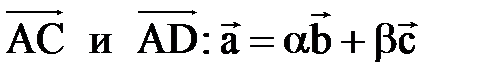 .
.
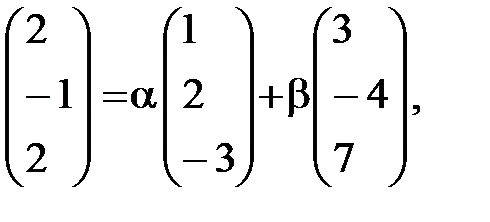
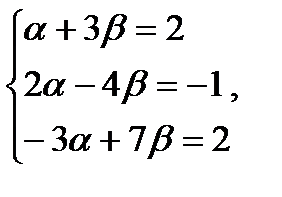 .
.
Решая эту систему, получим ответ: 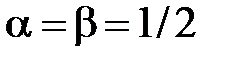 , т.е.
, т.е. 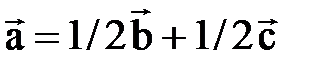 .
.
Задание 5.
