Бір Өлшемді гармоникалыҚ тҰзаҚтыҢ шектелген геометриясындаҒы екі дене кванттыҚ есебін шешу Әдістері

КІРІСПЕ

Қазіргі таңда молекулалар физикасы мен ультрасуық атомдар яғни, кванттық газдар физикасы 1995 жылы экспериментті түрде бозе-эйнштейн конденсациясы ашылғаннан бастап, дами бастады. Бұл бағыт бойынша эксперименттік жұмыстардың маңызы [1-3] артуда. Соңғы жылдардағы бұл облыстағы таңқаларлық эксперимент нәтижелері кішіөлшемді кванттық жүйені және қатты «оқшауланған»(немесе коррелирленген) көпбөлшекті жүйені зерттеуде тамаша мүмкіндіктерді ашып берді. Сонымен қатар, жеке молекулалар мен атомдарды гармоникалық тұзақта толықтай бақылау және бағалау мүмкіндігі анық көрсетілген.Молекулалар және ультрасуық атомдармен тәжірибе жасау кезінде бөлшектердің қозғалысы бір немесе екі айнымалы бойымен «оқшауландырылған» болып табылады.Оптикалық потенциалды қолдана отырып оның динамикасы жазықтықта орналасқандығын немесе сызықпен шектелгендігін анықтауға болады. Мұндай жағдайда, кіші өлшемді жүйелердің физикалық қасиеттері оптикалық тұзақтың әсерінен айтарлықтай өзгеруі мүмкін. Сондай-ақ, тұзақ параметрлерін өзгерте отырып, атомаралық әсерлесулерді тиімді басқаруға болады. Бұл күшті корреляцияланған кванттық жүйелерді [4], кіші өлшемді жүйелердегі азбөлшекті және көпденелі эффекттерді [2, 3], молекулаладың құрылуы кезіндегі жаңа механизмдерді [6], кванттық компьютер үшін мүмкін элементтерді [4] және т.б. зерттеу үшін жаңа мүмкіндіктер ашады.

Ультрасуық атомдар бойынша зерттеулер нәтижесі асқын аққыштық, асқын өткізгіштік [2], «Үлкен Жарылыстың» алғашқы кезінде пайда болған кварк-глюондық плазма, сонымен қатар кванттық компьютер элементтеріне қолданылатын молекулалардың пайда болуымен жүретін химиялық реакциялар [7,10], сияқты физикалық құбылыстарды басқарумен қатар оларды модельдеу мүмкіншілігіне байланысты қызығушылық тудырауда.

Бұл сала ауқымында жоспарланған зерттеулер әлемнің барлық үлкен ғылыми орталықтарында заманауи теориялық білімді дамытатын бағыттың бірі болып табылады. Бұл зерттеулер тек теориялық қызығушылық қана емес, сонымен қатар практикалық маңыздылығы зор- жаңа бағыт. Жоспарланған зерттеу нәтижелері ультрасуық атомдар мен молекулаларды зерттеуші эксперименттерді өңдеу мен жоспарлауға қажетті және маңызды. Себебі, қазіргі уақытта бұл бағыттағы теориялық моделдер эксперимент қажеттілігінен артта қалуда.

Осы уақытқа дейін пайдаланылған азбөлшекті кванттық құбылыстарды бейнелеуге негізделген теориялық модельдер [3,6] бұл саладағы заманауи тәжірибелердің қажеттіліктерін қанағаттандыра алмайды. Ультрасуық кванттық жүйелердің жан-жақты тәжірибелік шолулары осы молекулалардың қасиеттерін теориялық зерттеуді қажет етеді. Олардың интерпретациясы және жаңа тәжірибелерді жоспарлау үшін бар теориялық модельдерді жақсарту және жаңа теориялық модельдерді дамыту үшін жұмыстар жүргізілуі керек.

Көптеген теориялық зерттеулер негізінен бірөлшемді және екіөлшемді гармоникалық тұзақтардағы екіатомды жүйелердің шашырау параметрлеріне арналған қарапайым бірөлшемді жартылай аналитикалық М.Ольшано (1998 ж.) және Г. Шляпников (2001 ж.) моделдеріне негізділген [6-10]. Атомаралық әсерлесу ретінде бұл жұмыстарда жеңілдетілген дельта түрдегі потенциал қолданылады [8,9]. [12-15] жұмыстарында геометриясы шектеулі гармоникалық тұзақтың нақты әсерлесуі бар қосатомды жүйелерді сандық зерттеу әдістемелері дамытылған. Жаңа нәтижелер алынған (тұзақтағы кванттық шашыраудың өшу әсері байқалған, тұзақта екіатомды молекулалардың резонансты түзілуінің жаңа механизмі ұсынылған, т.б. ) және де тұзақ ангармонизмінің спектрге, азөлшемді кванттық жүйелердің шашырау параметрлеріне әсері сияқты киынырақ әсерлемелерді зерттеу үшін ыңғайлы “плацдарм” жасалған. Екінші жағынан, ангармонизм әсерін зерттеудің өзекті әрі тиімді әдісі болып осцилляторда өрнектелу[16] табылады. Бұл әдіс соңғы кездері отандық ғалымдармен [17] сәтті зерттелуде. Осы әдістеме ангармоникалық осциллятордың төмен орналасқан күйлерін есептеуге сәтті қолданбақшы. Екі әдістеме де бұл жұмыс барысында нақтырақ әсерлесуі бар түрлі конфигурациялы оптикалық тұзақтағы байланысқан күйлер мен екіатомдық кванттық және үшөлшемді моделдік жүйелер үшін шашырау параметрлерін есептеу ретінде өңделмекші.

Ғылыми жұмыс барысында зерттеудің негізгі әдістері ретінде осцилляторда өрнектелу әдістері [16-19] мен кішіөлшемді кванттық жүйелерді сандық зерттеу әдістері [12-15] қолданылады. Бұл екі әдістеме соңғы жылдары кванттық физиканың күрделі есептерін шешуде маңыздылығы мен қажеттілігін көрсетті. Әсіресе, гармоникалық тұзақта масса центрінде түрлі атомдардың соқтығысуының салыстырмалы қозғалысының әсерін қарастыруда төртөлшемді Шредингер теңдеуін сандық интегралдауға арналған арнайы әдіс қолдану дамытылған. Бұл әдістерді ангармоникалық атомдық тұзақта айнымалылары ажыратылмайтын масса центрі бар салыстырмалы қозғалыстағы екіатомды есептерге салыстырмалы қозғалыстағы екіатомды есептерге колданамыз. Осцилляторда өрнектелу үшденелі кванттық жүйелердің спектрін зерттеуге жақсы игерілген [19].

2. Оптикалық тұзақтың біртекті геометриясындағы екі атомның негізгі күйінің энергиясын есептеу

Бұл бөлімде E негізгі деңгей энергиясының және бірөлшемді гармоникалық тұзақта бұғауланған екі бозонды атомдардың сәйкес Ψ толқындық функцияларының (ТФ) атомаралық әсерлесу интенсивтілігінен тәуелділігін зерттеу қарастырылады. Бұл мәселе 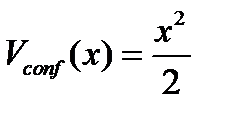гармоникалық потенциалдағы атомдардың салыстырмалы қозғалысының толқындық функциясы үшін нөлдік шекаралық шарты 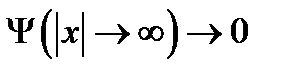болатын Шредингердің бірөлшемді теңдеуін (ШТ) шешуге келтіріледі:

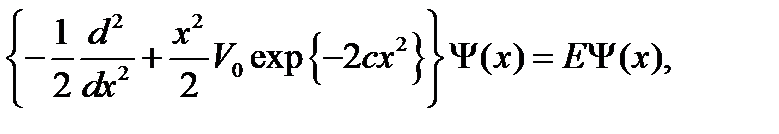(1.5.1)

Ол үшін осцилляторлық бірліктер жүйесін қолданайық, сол кезде энергиялар 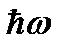бірлікте өлшенеді, ал ұзындықтар 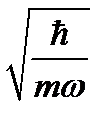бірлікте. Атомаралық әсерлесу 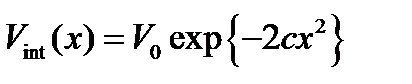екі параметрлік гаусстық потенциалмен модельденген [1], мұнда V₀-параметрі потенциалдық шұңқырдың тереңдігін береді, ал с потенциалдық шұңқырдың енін анықтайды. E және 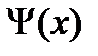шамаларының 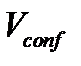тұзақтың ұстап тұру потенциалы болмаған кездегі 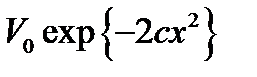бірөлшемді гаусстық потенциалда 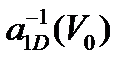кері шашырау ұзындығынан тәуелділігі зерттелді. Алғашында ШТ (1) сандық шешу кезінде 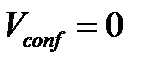жағдайы үшін үздіксіз спектр күйі E>0 үшін 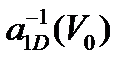тәуелділігі есептелді, ТФ үшін шекаралық шарты:

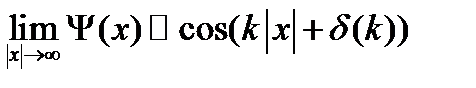, (1.5.2)

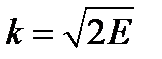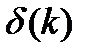мұндағы , ал - шашырау фазасы. Сонымен қатар, бірөлшемді шашырау ұзындығы келесідей анықталады:

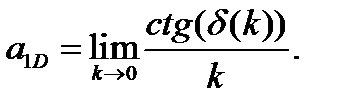(1.5.3)

Әсерлесу потенциалының әртүрлі параметрлері кезінде есептелген 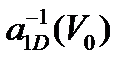тәуелділігі 1-суретте көрсетілген. Қысқа әсерлі потенциалда үшөлшемді шашырау ұзындығының ұқсас есебі [26] жұмыста жүргізілген.

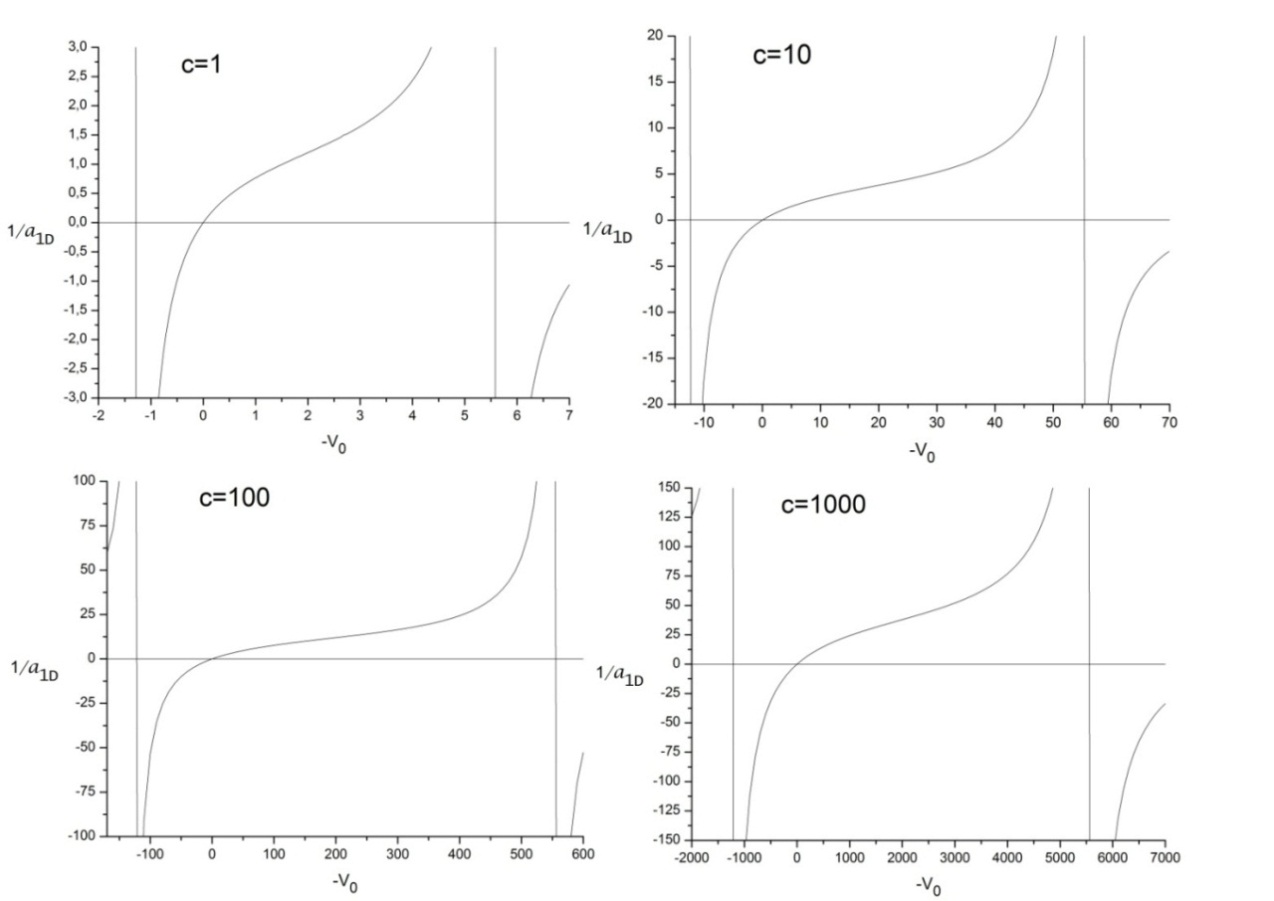
Сурет 1 – 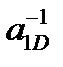кері шашырау ұзындығының 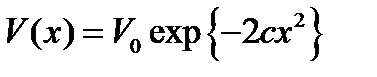потенциалдық шұңқырдың тереңдігінен және с параметрінен тәуелділігі

Есептерді меншікті мәндерінің шешімін алу үшін сандық есептеу әдісі, яғни (1) кері итерация әдісі қолданылды. ШТ-не (1) өрнектің құрамындағы туындыларды аппроксимациялау үшін екінші ретті дәлдікпен ақырғы-айырмалы аппроксимациялар қолданылды, олар h²-ретті қателікті қамтамасыз етеді, мұндағы h – айырмалы тордың қадамы. Есептеу нәтижелері 2-6 суреттерде көрсетілген, онда есептелген толқындық функциялардың мәндері де келтірілген. Есептеулердің негізгі нәтижелері 2- және 4-суреттерде келтірілген.

Графиктен (2-сурет) көріп тұрғанымыз, екі атомның 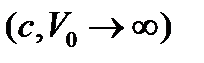әсерлесу потенциалын бір уақытта тарылту және тереңдету кезінде, яғни 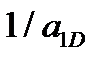диапазонда графикте көрсетілген қысқа әсерлі әсерлесуге ауысу кезінде, үйлесімді нәтиже аламыз (берілген 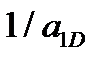диапазонда c=100 және c=1000 арасындағы айырмашылық әрең білінеді). Осы нәтижені [27] жұмыстың нәтижесімен салыстырған кезде 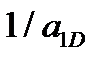оң мәндері аумағында өсетін қисықтардың сәйкес келмеуін байқаймыз. шегінде гаустық потенциал [27] жұмысында қолданылған нөлдік радиус потенциалына (псевдопотенциалға) сапалы түрде ұмтылады.

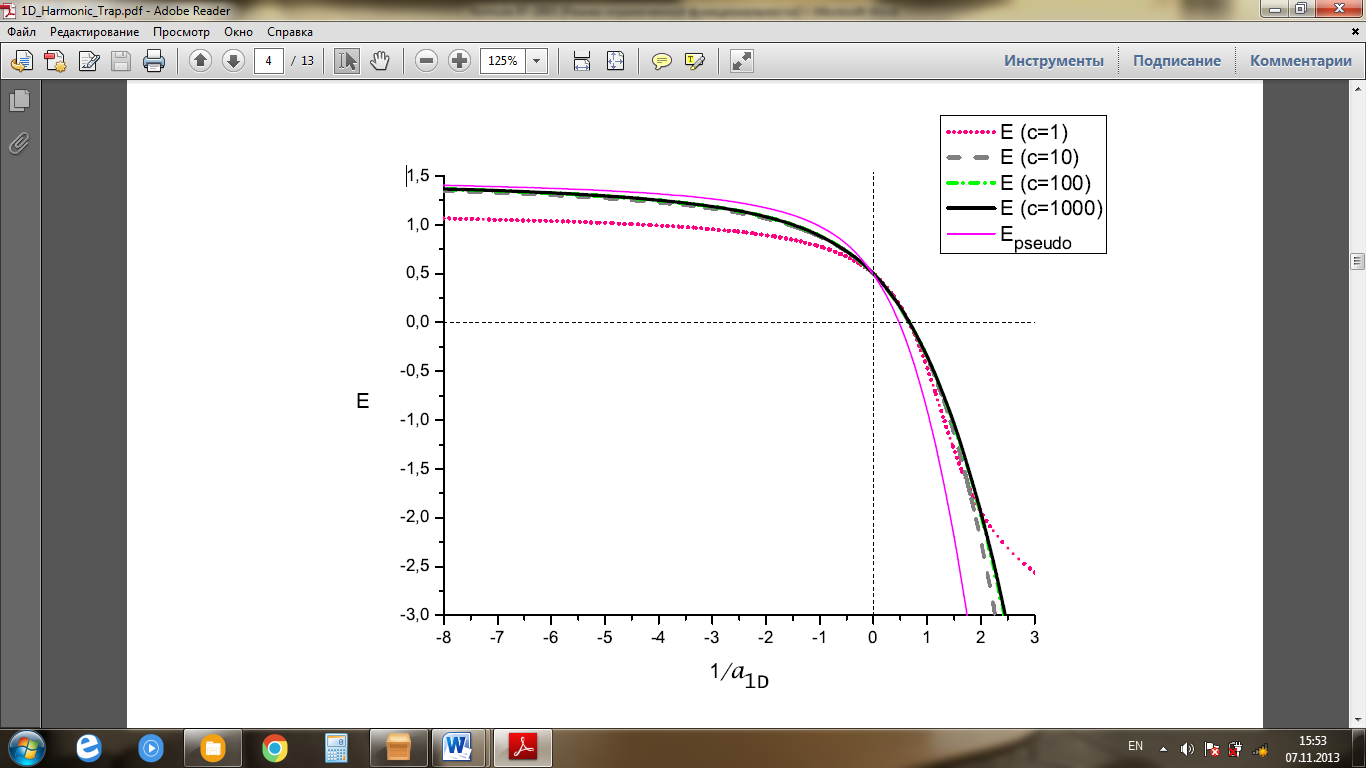
сурет 2 – Әртүрлі c кезіндегі негізгі күй энергиясы, E_pseuda - [27] жұмыста есептелген дельта-функция түріндегі түйіскен әсерлесу жағдайындағы энергия

Жуырдағы тәжірибеде [5] 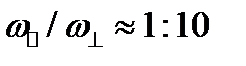бойлық жиіліктің көлденең жиілікке қатынасымен сигара тәрізді үшөлшемді потенциалдағы бірөлшемді геометрия жүзеге асырылды. [5] жұмыстың авторлары оптикалық дипольді тұзақпен және магниттік өріс градиентімен құрылған, потенциалдағы спиндері қарама-қарсы бағытталған екі фермионның жүйесін зерттейді. Зерттеу аймағы энергия мәні 1.5 сәйкес келетін негізгіден екінші қозған күйге ауысу нүктесінің аймағында. Тәжірибе жүргізіліп отырған кері шашырау ұзындығының диапазоны негізгі күй үшін, шамамен, -2.03: ≤ -2.03 мәнінен басталады; екінші қозған күй үшін: ≥ 2.03.

БІР ӨЛШЕМДІ ГАРМОНИКАЛЫҚ ТҰЗАҚТЫҢ ШЕКТЕЛГЕН ГЕОМЕТРИЯСЫНДАҒЫ ЕКІ ДЕНЕ КВАНТТЫҚ ЕСЕБІН ШЕШУ ӘДІСТЕРІ

Қарастырылып отырған есептердің сандық талдануы үшін, бұрыштық айнымалылар бойынша дискретті торда құрастырылған арнайы екіөлшемді базисті қолдана отырып, Шредингердің үшөлшемді теңдеуін сандық интегралдау үшін [13-15] жұмыстарда берілген әдісті қолданамыз. Мұнда біз стационарлы және стационар емес жағдайларға әдістің негізгі бөлігін баяндаймыз.

Бірінші координаталары r_1, r₂ және массалары 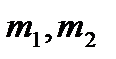болатын екі әртүрлі атомның динамикасын 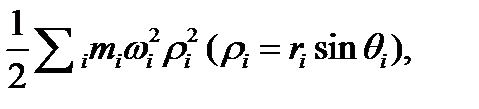гармоникалық потенциалда қарастырамыз, ол Шредингердің стационар емес теңдеуімен бейнеленеді

Гамильтонианы

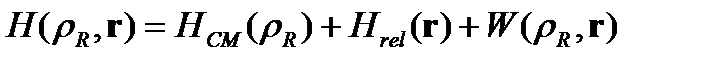(1.1)

мұнда

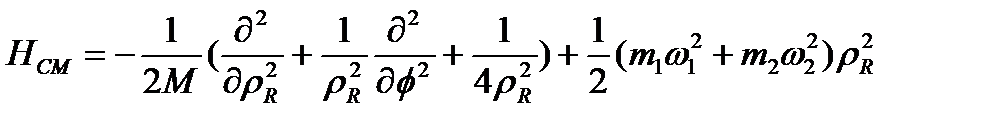(1.2)

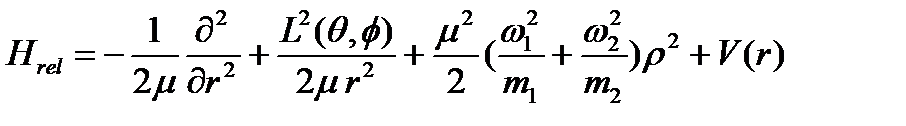(1.3)

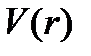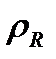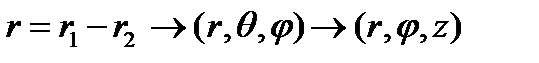гамильтониандары массалар орталығының қозғалысын және атомдардың салыстырмалы қозғалысын сипаттайды. -потенциалы атомаралық әсерлесуді бейнелейді, және массалар орталығының және салыстырмалы қозғалыстың полярлық координаталары және , .

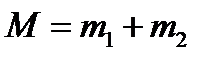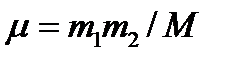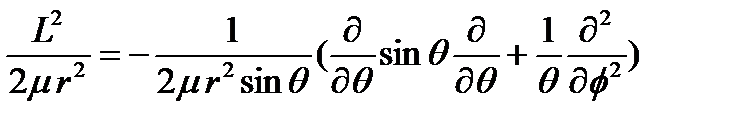
қосылғышы атомдардың салыстырмалы қозғалысының кинетикалық энергия операторының бұрыштық бөлігін көрсетеді.

Қосылғышта

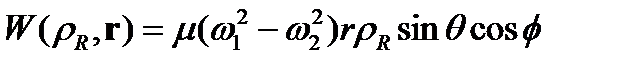(1.4)

бар болуы (1.1) гамильтонианында гармоникалық тұзақтың көлденең ұстап тұратын потенциалындағы массалар орталығы мен атомдардың салыстырмалы қозғалыс айнымалыларының бөлінбеуіне әкеледі, өйткені айырмалы атомдар жағдайында әрбір атом өзінің меншікті жиілігін 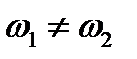“сезеді”. (1.4) теңдігінен шығатыны, 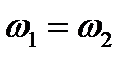бірдей атомдар жағдайында, 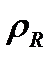және 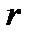айнымалылары бөлінеді де мәселе айтарлықтай жеңілдейді.

Бұл жұмыс оптикалық тұзақтың ангармонизм эффекттерін ескеруге бағытталған, бұл жағдайда массалар орталығының және салыстырмалы қозғалыстың айнымалылары 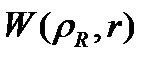операторында бөлінбейді, және тіпті бірдей атомдар жағдайында, дегенмен (1.4) оператор құрылымы гармоникалық тұзақ жағдайынан өзгеше. Ангармоникалық тұзақтың басқа маңызды ерекшелігі – атомдардың тұзақ қабырғалары арқылы туннельдену мүмкіндігі [28].

Шредингер теңдеуін интегралдау 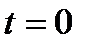-ден 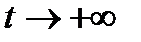асимптотикалық аймаққа дейін толқындық пакет үшін мынадай бастапқы шартпен орындалады:

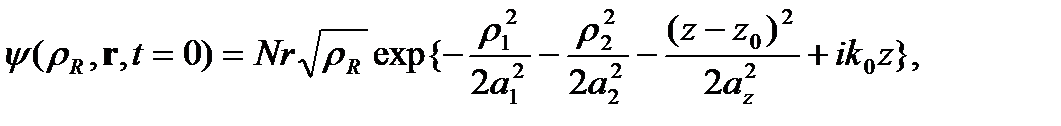(1.5)

Ол 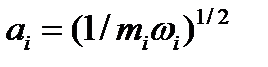бар көлденең тұзақтың негізгі күйіндегі екі әсерлеспейтін атомдарды көрсетеді, мұндағы 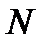нормалау шартымен 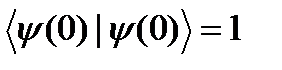анықталады. Мұндай бастапқы шарт салыстырмалы соқтығысу жылдамдығы 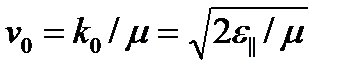болған кезде атомның атомда шашырауын зерттеуге мүмкіндік береді (анықталатын бойлық соқтығысу энергиясы 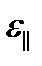). 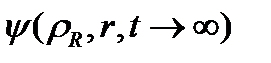шашыраған толқындық пакетті зерттей отырып, асимптотикалық аймақтағы шашырау параметрлерін анықтауға, сонымен қатар екіатомдық молекулалардың пайда болу ықтималдығын анықтауға болады. Атомдардың тұзақпен әсерлесуінің ангармоникалық потенциалы жағдайында тұзақтың бүйір қабырғасы арқылы (соңғы енінің потенциалы), тұзақтың квази-еркін атомдары арқылы, сонымен қатар, екіатомдық молекулалардың байланысқан күйлері арқылы (яғни тұзақтағы атомдық және молекулалық деңгейлер енін бағалау) туннельдеу ықтималдығын есептеу қызығушылық тудырады. Бұл жағдайдағы бастапқы жуықтау болып 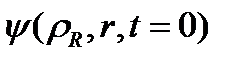тұзақтағы атомдық немесе молекулалық күйлер алынады.

1.1 Бұрыштық айнымалыларды дискреттеу: 2D дискретті айнымалылар көрінісінің тура емес туындысы

Бұл әдісте 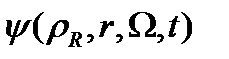шешімін жіктелу түрінде іздейміз

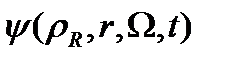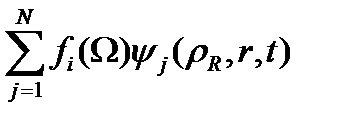= (1.1.1)

екіөлшемді базис бойынша

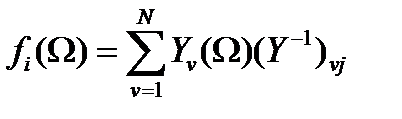(1.1.2)

тордағы берілетін түйіндер 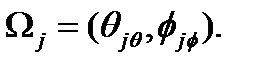Θ айнымалысы үшін, түйін нүктелері Лежандр полиномдарының нөлдерімен сәйкес келеді. φ айнымалылары бойынша, түйін нүктелері формуламен беріледі.

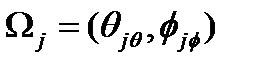Түйін нүктелерінің толық саны (1.1.1) жіктелуіндегі базистік функциялардың санына және (1.1.2) өрнегіндегі қосылғыштардың санына тең, мұндағы ν символы {l,m} екіөлшемді символ болып табылады, ал ν бойынша қосынды екі қосындыны береді

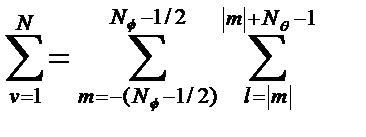(1.1.3)

l- және m-индекстері Θ және φ полином айнымалылары бойынша нөлдер санына тең, олар төменде анықталған. (7)-дегі коэффициенттері тордағы берілген полиномдарға кері N×N өлшемді матрица элементтері болып табылады. Мұндай анықтаулар кезінде, (2.1.1) жіктелуіндегі 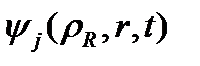коэффициенттері 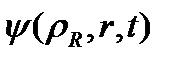тордағы түйін нүктелеріндегі бастапқы функцияның мәндері болып табылады, бұрыштық айнымалы бойынша : =

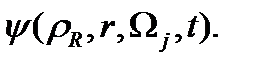
(1.1.2) теңдеуіндегі полиномдар мына формула бойынша құрылады

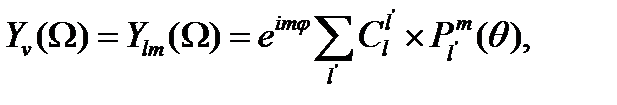(1.1.4)

бұл жалпы жағдайда, қарапайым сфералық гармоникалармен сәйкес келеді, тек үлкен ν үшін, ортогоналдылық шарты орындалады

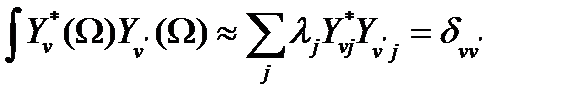(1.1.5)

барлық ν және ν' ≤N. Мұнда 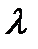коэффициенті тұрақты коэффициентке көбейтілген Гаусс бойынша сандық интегралдаудың стандартты салмағы болып табылады.

Бұл жағдайда матрица ортогональ болып табылады, және бұл полиномдардың ерекшелігі (1.1.4) төменде (1.1-1.5) есебін интегралдау үшін компонентті ыдыраудың эффективті есептеу сызбасын құру үшін қолданылады.

1.2 Шредингердің стационар емес төмен өлшемді теңдеуін шешу үшін компонентті жіктеу әдісі

Дискретті айнымалының түзу емес туындысының (ДАТЕТ) жағымды қасиеті (1.1.1-1.1.5) бұл көріністе гамильтонианның кинетикалық энергиясының операторындағы бұрыштық бөлігі ғана диагонал емес болып қалады (1.1) ((1.2-1.4) қараңыз)

,

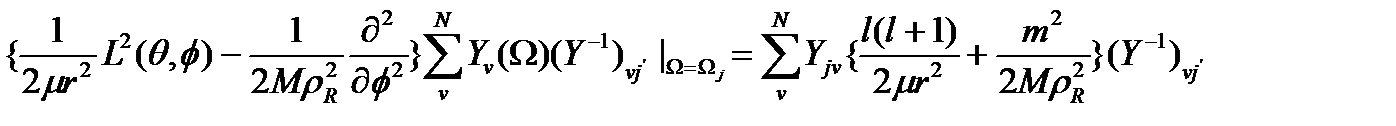ол қарапайым унитарлы түрлендіру көмегімен диагоналдануы мүмкін. Бұл қасиет Шредингер теңдеуін интегралдау үшін тиімді алгоритм құру үшін қолданылады, оның есеп уақыты қарапайым дифференциал теңдеулер жүйесіндегі белгісіз сандардың өсуімен сызықты түрде өседі

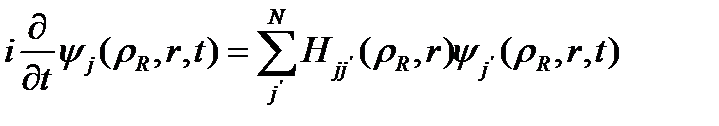(1.2.1)

жеке туындылардағы бастапқы төменөлшемді Шредингер теңдеуін ДАТЕТ көрінісінде жуықталады.

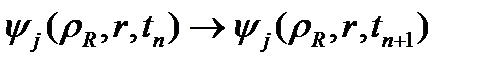қадамын уақыт бойынша сандық жуықтау үшін Г.И.Марчуктің компонентті бөлшектеу әдісіне негізделген есептеу сызбасы өңделген. Бұл әдісте гамильтониан (1.1) үш бөлшекке ыдырайды:

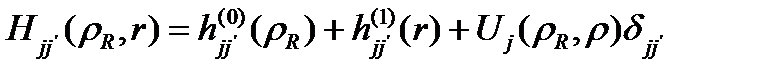(1.2.2)

мұндағы

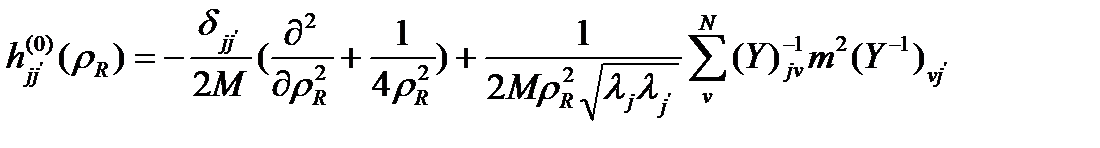
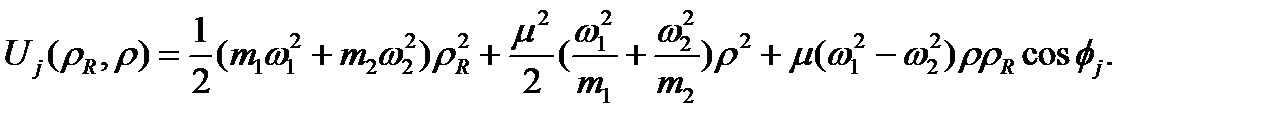
Сонымен қатар, мұнда, уақыт бойынша қадам , келесі түрде жуықталады

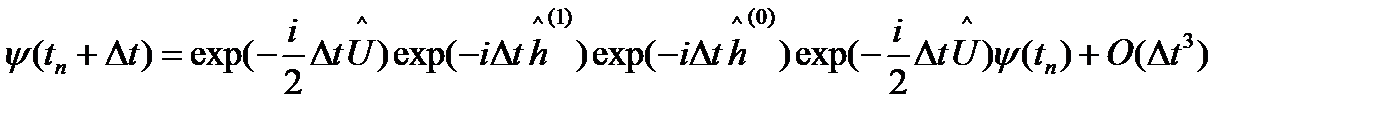(1.2.3)

Бұл сызбада ДАТЕТ ((1.1.2) функциялары) U операторы үшін диагоналды көрініс береді, ал көрінісі ((1.1.4) функциялары) - және операторлары үшін диагоналды көрініс беретіні туралы факт қолданылады. Бұл жағдай тиімді алгоритм тұрғызуға мүмкіндік береді, онда есептеу уақыты бұрыштық айнымалы бойынша әртүрлі торлардың түйінді нүктелерінің санының өсуімен сызықты өседі. Үшөлшемді Шредингер теңдеуі (екі бұрыштық және бір радиалды айнымалылар) үшін жүргізілген тесттік есептеу бұл тұжырымды растайды. Бұл есептеу 3-суретте бейнеленген, мұнда есептеу сызбасында және қарапайым Кранк-Николсон әдісінде есептеу уақыты салыстырылған, екіншісінде есептеу уақыты бұрыштық айнымалылар бойынша N түйін нүктелері санының өсуімен өседі.

Өңделген есептеу сызбасы және оның нұсқалары осы жұмыс аясында зерттелетін төмен өлшемді кванттық есептерді сандық талдау үшін пайдаланылады.

Үздік сызық Кранк-Николсон алгоритміне сәйкес келеді, ал тұтас сызық компонентті ыдырауға сәйкес келеді (2.2.3).

Сурет 3 – Есептеу уақытының (CPU time) (2.2.1) жүйесіндегі N теңдеулер санынан тәуелділігі

1.3 Төмен өлшемді кванттық жүйелердегі шашырау параметрлері мен спектрлерін сандық зерттеу әдісі

Алдыңғы бөлімдерде (1.1-1.2) көрсетілген есептеу сызбасы гармоникалық тұзақтың шектеулі геометриясындағы атомдардың соқтығысуы кезіндегі шашырау параметрлерін есептеуге бағытталған. Ол сондай-ақ ангармоникалық тұзақтан туннелдеу эффекттерін зерттеуге мүмкіндік береді.

Жұмыстың басқа маңызды мәселесі – тұзақ ангармонизмінің тұзақтағы молекулалық (екіатомды молекулалар) және атомдық спектрлерге әсерін зерттеу. Қарастырылып отырған есептеу сызбасының модификациясы бұл мәселені зерттеуге мүмкіндік береді. Меншікті мәндеріне есепті шешу үшін (1.1-1.4) гамильтонианы үшін [15] жұмысында берілген спектрлік әдіс қолданылады. Бұл әдіс 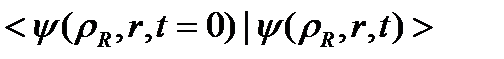корреляциялық функциясын есептеуге негізделген, мұндағы 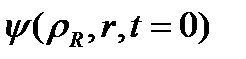бастапқы күйді спектрдің туынды тесттік функциясы ретінде таңдауға болады [14]. Ал стационар емес Шредингер теңдеуінің 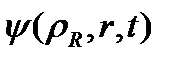шешімі (1.1-1.4) гамильтонианмен жоғарыда қарастырылған сандық әдіс көмегімен анықталады.

(1.1-1.4) түрдегі гамильтонианмен ангармоникалық тұзақтағы кванттық жүйелердің төменөлшемді спектрін есептеу үшін төмендегі Шредингер түріндегі қарапайым дифференциалдық теңдеулер жүйесінің шешімін сандық зерттеуді жоспарлаймыз

(1.3.1)

ДАТЕТ көрінісінде жеке туындылардағы бастапқы төменөлшемді Шредингер теңдеуін жуықтайды. Мұнда

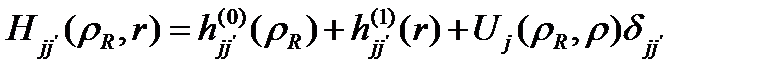(1.3.2)

мұндағы

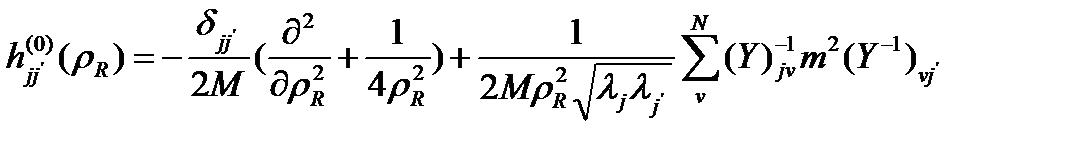
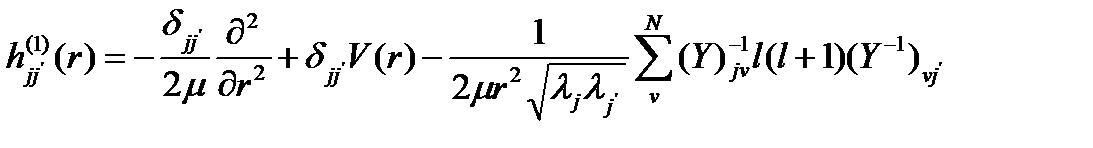
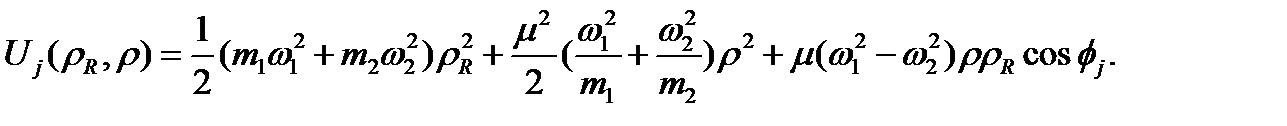
(1.3.2) теңдеуін сандық интегралдау үшін есептеу математикасының стандартты әдістерін қолдану жоспарлануда: радиал туындыларды жуықтау үшін жоғарғы ретті ақырғы айырым әдісі және ішкі кеңістіктегі кері итерация алгоритмі.