Свободные колебания систем с одной степенью свободы

Простейшей колебательной системой, с одной степенью свободы может служить груз, подвешенный на вертикально расположенной пружине (рис. 2.6).

Дифференциальное уравнение колебаний груза 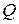получим, взяв сумму проекций всех сил (включая силы инерции согласно принципу Даламбера) на вертикальную ось, в виде

.

Отсюда

,

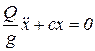или

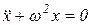. (2.2)

где x – вертикальное перемещение груза от положения статического равновесия; 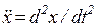, 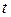– время; 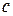– жесткость пружины; 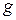– ускорение свободного падения; 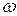– угловая частота свободных колебаний

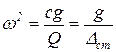; (2.3)

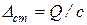– величина удлинения пружины при статическом действии груза .

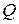Решением уравнения (2.2) будет

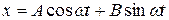, (2.4)

где А и В – постоянные интегрирования, зависящие от начальных условий.

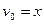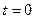Если заданы начальная координата груза x₀ и начальная скорость при , то из (2.4) определим

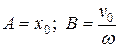. (2.5)

Полагая 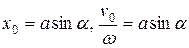(2.6)

решение (2.4) можно представить в виде ,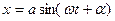

где а — амплитуда колебаний, определяемая формулой

.

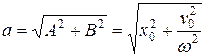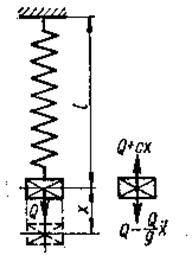
Рисунок 2.7 – Модель простейшей колебательной системы

Величина 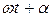называется фазой колебаний, а величина α — сдвигом фазы. На основании (2.6) α, может быть определено из условия

.

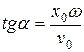Угловая частота колебания (число колебаний, совершаемое в течение 2π секунд) на основании (2.3) будет

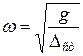(2.7)

Или ,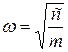

где 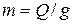— масса подвешенного груза.

Зная угловую частоту, можно определить период колебаний

.

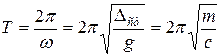Число колебаний в секунду, т. е. секундная частота, выражаемая в герцах, определится формулой

.

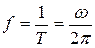При колебаниях груза, подвешенного на конце пружины, представляющей собой стержень длиной l с жесткостью поперечного сечения на растяжение EF и жесткостью

,

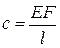собственная частота колебаний согласно (2.7) определится формулой

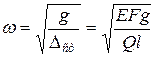. (2.10)

Учитывая, что 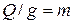, можно записать

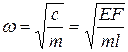. (2.11)

Из формул (2.10) и (2.11) видно, что частота свободных колебаний системы при неизменной массе возрастает с увеличением жесткости и уменьшается с увеличением массы при неизменней жесткости. Отношение частот свободных колебаний грузов, прикрепленных к концам двух разных стержней, обратно пропорционально корню квадратному из отношения статических удлинений стержней.

Примером системы с одной степенью свободы может служить также колебательная система, состоящая из массивного диска, прикрепленного к нижнему концу жестко закрепленного верхним концом вала (рис. 2.8). Если к диску в его плоскости приложить и внезапно удалить пару сил, то возникнут свободные колебания кручения вала вместе с диском. Обозначим крутильную жесткость вала (крутящий момент, вызывающий закручивание вала на один радиан) через с:

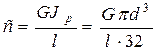, (2.12)

где G — модуль упругости при сдвиге; d — диаметр вала; l — длина вала.

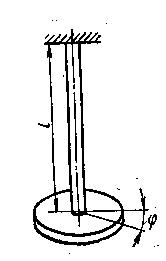
Рисунок 2.8 – Система с одной степенью свободы

Воспользовавшись принципом Даламбера (инерцией массы стержня пренебрегаем), получим дифференциальное уравнение крутильных колебаний диска, приравняв крутящий момент cφ, действующий в ва­ле при его закручивании на угол φ, моменту сил инерции массы диска:

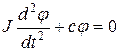, (2.13)

где J — момент инерции диска относительно оси стержня, перпендикулярной к плоскости диска.

Для диска постоянной толщины h, изготовленного из материала с удельным весом γ, получим

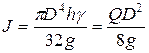. (2.14)

Здесь D – диаметр диска; Q — вес диска.

Для диска переменной толщины

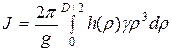. (2.15)

Обозначив

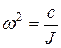, (2.16)

уравнение (2.13) перепишем в виде

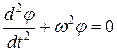. (2.17)

Общее решение этого уравнения будет

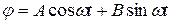. (2.18)

Период колебаний рассматриваемой системы

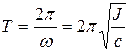. (2.19)

Для стержня постоянного диаметра d с учетом (2.12) имеем

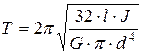, (2.20)

а частота колебаний

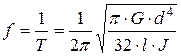. (2.21)