Теория метода. В идеальном колебательном контуре (рис

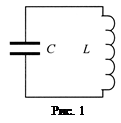
В идеальном колебательном контуре (рис. 1) ак­тивное сопротивление R = 0 и потери электромагнитной энергии отсутствуют. Сила тока в контуре, заряд в конденсаторе. ЭДС самоиндукции в катушке и ряд других ха­рактеристик совершают незатухающие колебания с собственной циклической частотой

,

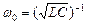т.е. с периодом, определяемым по фор­муле Томпсона:

.

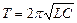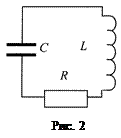
В реальном колебательном контуре (рис. 2), состоящем из по­следовательно соединенных конденсатора (емкостью С), катушки (индуктивностью L) и резистора (сопротивления R),процесс из­менения величины заряда с течением времени t описывается дифференциальным уравнением, составленным на основании второго закона Кирхгофа:

.

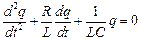Если ввести обозначения коэффициента за­тухания 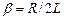и собственной частоты 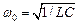,то дифференциальное уравне­ние затухающих колебаний в контуре:

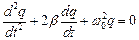
Решением этого дифференциального урав­нения, является функция, определяющая величину заряда :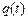

.

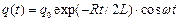Чтобы найти силу тока, продифференцируем полученное решение по времени:

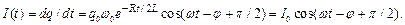
Стоящий перед косинусом множитель 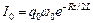представляет собой амплитуду, которая экспоненциально умень­шается с течением времени. Величина 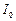- это начальная ампли­туда в момент времени 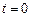. Циклическая частота затухающих колебаний:

,

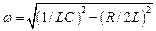несколько меньше собственной частоты колебаний в идеальном контуре, которая равна: 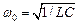. Вид функции 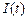говорит о том, что в контуре, содержащем активное сопротивление 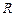, про­исходят затухающие колебания с частотой .

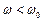В зависимости от соотношения между параметрами 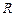, , 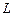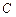возможны четыре варианта процессов в контуре.

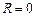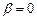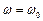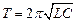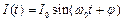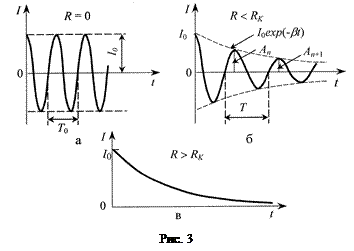
1. Если , коэффициент затухания тоже равен нулю , то , , ,где 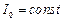. Значит, в контуре происходят незатухающие гармонические колебания (рис. 3 а).

2. Если 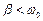, следовательно 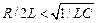или 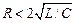(вели­чина 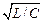называется волновым сопротивлением контура), то в контуре наблюдаются затухающие колебания с частотой 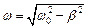(рис. 3 б).

3. Если окажется, что 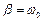, т.е. , то математиче­ски получается, что значение 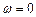и в контуре колебания не воз­никают, а наблюдается апериодический процесс. Активное со­противление 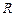, удовлетворяющее условию , называ­ют критическим сопротивлением контура 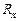(рис. 3 в).

4. Если же 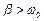, т.е. если 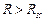, то 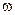- мнимая величина, а это математически тоже говорит об отсутствии колебательного процесса, апериодическом стремлении 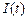к нулю (рис. 3 в).

Интенсивность затухания колебаний характеризуется лога­рифмическим декрементом затухания, определяемым как лога­рифм отношения двух последующих амплитуд затухающих коле­баний (см. рис. 3 б):

,

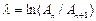где 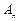- амплитуда колебаний в некоторый момент времени 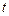, 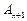амплитуда колебаний в момент времени 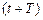. Поскольку 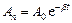и 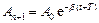, после подстановки значений амплитуд логарифмический декремент затухания:

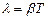
и зависит только от значений коэффициента затухания 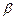и перио­да 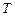. Часто используют характеристику, называемую добротно­стью контура 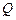. По определению добротность величина обратная логарифмическому декременту затухания

,

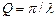она может бытьпредставлена в виде:

,

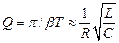если 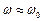,. т.е. 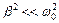. По величине добротности 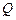судят о резонансных свойствах контура. При высокой добротности резо­нансный пик высокий, острый. Контур имеет хорошую частот­ную избирательность.