Оператор оценивания МНК для многофакторной модели линейной регрессии
Редко поведение зависимой переменной объясняется только с помощь одной независимой переменной. В действительности каждое явление определяется действием целого комплекса причин, поэтому несколько независимых переменных, используемых в комбинации, предлагают лучшее объяснение.
Истинная взаимосвязь между результирующим показателем (зависимой переменной) Y и различными объясняющими переменными Xj выражается так:
Y = b0 + b1X1 + b2X2 +…+bpXp + e,
или в матричном виде Y = Хb + e,
где Y – вектор значений зависимой переменной; Х – матрица значений независимой переменной размерностью (n ´ (p+1)); n – количество наблюдений; (p+1) – количество независимых переменных, включая значений фиктивной переменной Х0, тождественно равной единице (или число оцениваемых параметров); b –вектор параметров модели; e -вектор возмущения:
; 
; 
; 
.
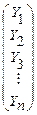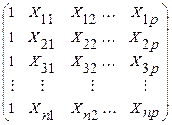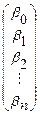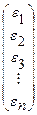Однако, как и в случае простой линейной регрессии, мы не знаем истинную зависимость и вынуждены находить оценки:
.
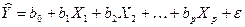Многофакторная оценочная регрессионная модель в матричном виде представляется следующим образом:
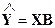,(2.16)
где B = {b0,b1,…,bp}` -транспонированный вектор оценок параметров модели;
Для оценивания параметров множественной регрессии применим методом наименьших квадратов. Остатки регрессии представим как разность фактических и теоретических (расчетных) значений результирующей переменной Y:
е = Y -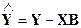 
.(2.17)
Тогда сумму квадратов остатков можно записать так:
,
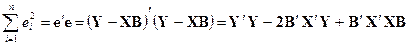где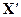 
- матрица, транспонированная к матрице Х.
Продифференцировав это выражение по Ви приравняв производную нулю, получим:
,
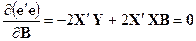или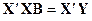 
. (2.18)
Отсюда имеем:
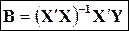. (2.19)
Уравнение (2.18) дает матричную форму записи системы нормальных уравнений, а формула (2.19) показывает, что вектор Вявляется решением системы таких уравнений.
В формуле (2.19):
, 
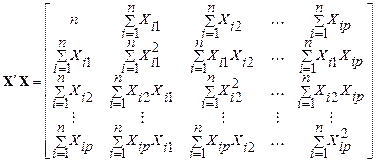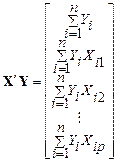
Для матрицы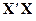 
по известным правилам ищется обратная матрица 
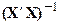, которая затем умножается на матрицу 
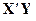, в результате чего определяются оценки параметров эконометрической модели В.
Если значения независимых переменных Хj в матрице Х представлены как отклонения от своего среднего (в центрированном виде), то матрицу ( 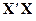) называют матрицей моментов. На ее главной диагонали расположены числа, характеризующие величину дисперсии независимых переменных, недиагональные элементы соответствуют взаимным ковариациям.
Коэффициенты bj (j = 1,2,…,р) представляют собой частные производные Y по соответствующим Хj:
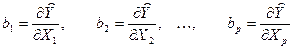
и показывают, насколько в среднем изменится величина Y при изменении соответствующего фактора Х на единицу и при неизменных значениях других факторов.
Вспомним, что в случае простой регрессии постоянная регрессии b0 представляла собой величину зависимой переменной при нулевом значении независимой переменной. Во множественной регрессии толкование постоянной является более сложным. В некоторых моделях свободный член оценивается a priori, в других случаях значимая постоянная может представлять средний эффект, оказываемый на Y любыми независимыми переменными, которые не были включены в модель.
Пример.Посмотрим, как использовать полученные формулы на нашем примере, в котором предполагалось, что объем продаж некоторого товара является линейной функцией затрат на рекламу. Добавим вторую независимую переменную, доход, (Х2), и запишем исходные данные в таблицу 3, которые используем для оценивания параметров следующей эконометрической модели:
Y = b0X0 + b1X1 + b2X2 + e.
Таблица 3
| i | Yi | Xi0 | Xi1 | Xi2 | Yi2 | X2i1 | X2i2 | Xi1Xi2 | Xi1Yi | Xi2Yi |
| å |
Оценивание выполним с использованием оператора МНК: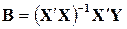 
.
;
; 
.
.
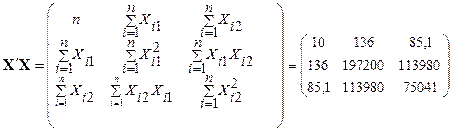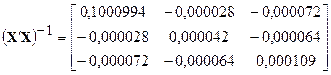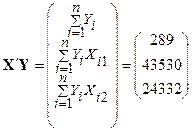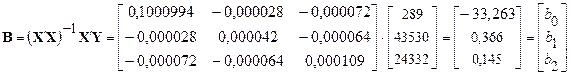Итак, получили модель: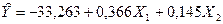 
.
Коэффициенты регрессии показывают, что увеличение затрат на рекламу на 1 грн. при неизменной величине дохода способствует росту объема продаж в среднем на 0,366 тыс. грн. Если же при неизменном уровне затрат на рекламу доходы возрастут на одну денежную единицу, увеличение объема продаж составит в среднем 0,145 тыс. грн.
Подставив в эту модель фактические значения независимых переменных, получим расчетные значения результирующего показателя Y (объема продаж):
.
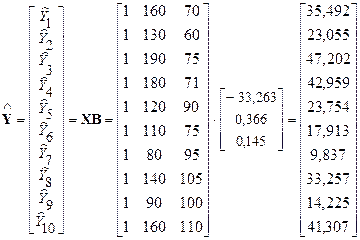Вектор остатков: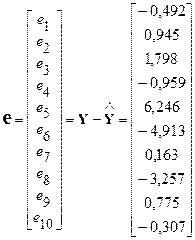 
.
Сумма квадратов остатков = е`е =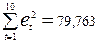 
.