Векторные диаграммы переменных токов и напряжений

Из курса математики известно, что любую синусоидальную функцию времени, на­пример i(t)=I_msin(wt+a), можно изобразить вращающимся вектором при соблюдении следую­щих условий :

а) длина вектора в масштабе равна амплитуде функции I_m ;

б) начальное положение вектора при t = 0 определяется начальной фа­зой a ;

в) вектор равномерно вращается с угловой скоростью w, равной угло­вой частоте функции.

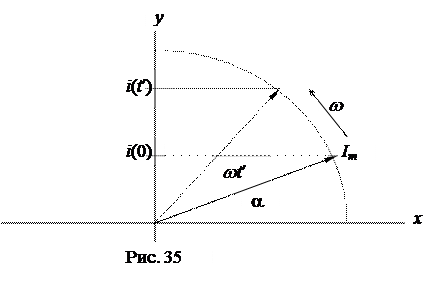При соблюдении названных условий проекция вращающегося вектора на вертикаль­ную ось y в системе координат х-у в любой момент времени t¢равна мгновенному значению функции i(t¢), следовательно i = I_m sin(wt+a)

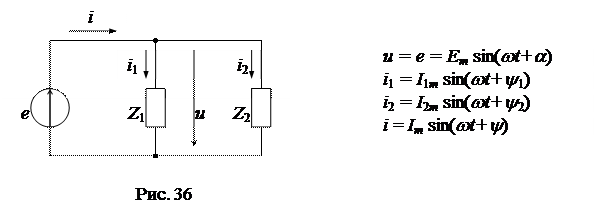
Рассмотрим процессы в схеме электрической цепи рис. 36. Изобразим си­нусоидаль­ные функции токов и напряжений вращающимися векторами для произвольного момента времени, например t = 0 (рис. 37а). При рассмотрении установившегося режима в схеме мгно­венные значения функций не представ­ляют интереса, поэтому момент времени, для которого строится векторная диа­грамма, может быть выбран произвольно. Целесообразно один из век­торов принять начальным или исходным и совместить его на диаграмме с одной из осей ко­ординат (вектор Е на рис. 37б совмещен с осью y), при этом остальные векторы располагают по отношению к исходному вектору под углами, равными их сдвигам фаз.

Так как на практике интерес представляют действующие значения токов и напряже­ний, то на векторных диаграммах длины векторов принимают рав­ными в выбранных мас­штабах их действующим значениям (рис. 37б).

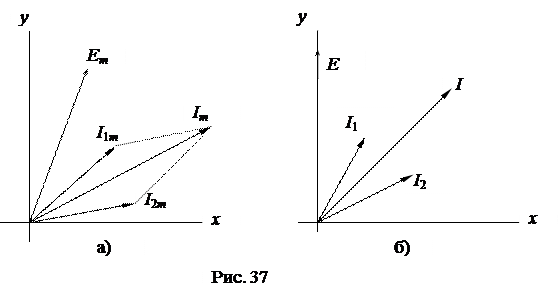Совокупность векторов, характеризующих процессы в цепи перемен­ного тока, по­строенных в выбранных масштабах и с соблюдением правильной их ориентации друг отно­сительно друга, называется векторной диаграммой.

Теоретические основы комплексного метода расчета цепей

Переменного тока

Из курса математики известно, что комплексное число Z может быть представлено в следующих трех формах: показательной, тригонометрической и алгебраической:

показательная тригонометрическая алгебраическая

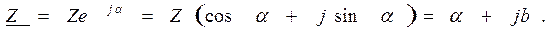
В основе перехода от одной формы комплексного числа к другой лежит известная из математики формула Эйлера :

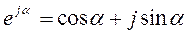
Здесь обозначены:

j = 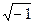– мнимое единичное число,

Z – модуль комплексного числа,

a - аргумент комплексного числа,

а – вещественная часть комплексного числа,

jb – мнимая часть комплексного числа.

Соотношения между коэффициентами различных форм комплексного числа выте­кают из формулы Эйлера :

a = Z cosa ; b = Z sina ; Z = 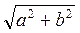; a = arctg .

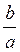Приведем наиболее часто встречающиеся численные соотношения :

e^j0 = 1 ; e^{± j180°} = -1 ; e ^j90° = +j ; e^-j90° = -j ;

1/j = -j ; j² = -1 ; j³ = -j ; и т.д.

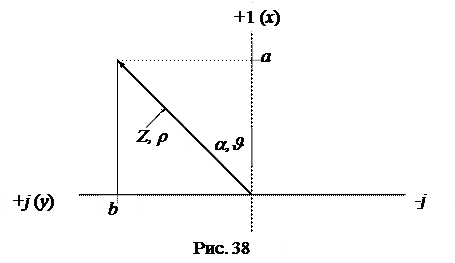Комплексное число Z = Z e^ja = a + jb может быть изображено векто­ром на ком­плексной плоскости (рис. 38), при этом алгебраической форме числа 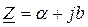соответствует декартовая система координат (a ® x; b ® y), а показа­тельной форме числа Z = 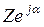- по­лярная система координат (Z ® r; a ® q).

Можно утверждать, что каждой точке (вектору) на комплексной плоско­сти соответ­ствует определенное комплексное число, и наоборот, каждому ком­плексному числу соответ­ствует определенная точка (вектор) на комплексной плоскости.

Известно, что синусоидальную функцию можно изобразить вектором, а вектор в свою очередь можно представить комплексным числом. Таким обра­зом, синусоидальные токи и напряжения, характеризующие установившийся режим цепи переменного тока, могут быть представлены комплексными чис­лами :

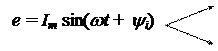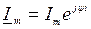Û - комплексная амплитуда,

Û 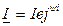- комплексное действующее значение. Здесь Û -знак соответствия.

При расчете цепей переменного тока возникает необходимость выпол­нения различ­ного рода математических операций с синусоидальными функ­циями. При замене синусои­дальных функций (оригиналов) комплексными чис­лами (изображениями) соответствующие математические операции выполня­ются с комплексными числами.

Сложение (вычитание) комплексных чисел производится в алгебраиче­ской форме

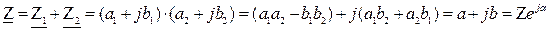
Умножение комплексных чисел может выполняться, как в алгебраиче­ской, так и в показательной формах:

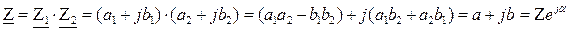
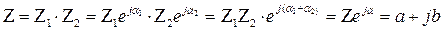
Деление комплексных чисел может выполняться как в алгебраической, так и в пока­зательной формах:

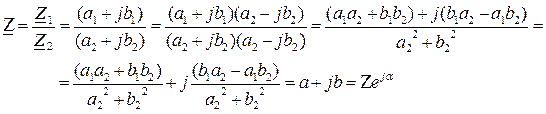
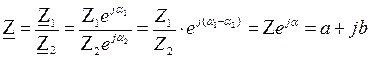
Возведение в степень (извлечение корня) комплексного числа выполня­ется только в показательной форме:

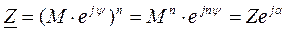
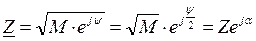
Установим порядок дифференцирования и интегрирования синусои­дальных функций в комплексной форме. Пусть задана некоторая функция тока и ее комплексное изображение:

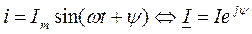
Производная и интеграл от этой функции их комплексные изображения будут равны:

;

.

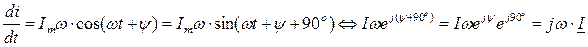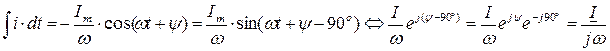Таким образом, дифференцированию синусоидальной функции времени соответст­вует в комплексной форме умножение ее комплексного изображения на множитель jw, а ин­тегрированию – соответственно деление на тот же коэф­фициент:

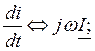
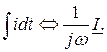
Замена математических операций 2-го рода (дифференцирование, интег­рирование) операциями 1-го рода (умножение, деление) существенно упрощает расчет цепей перемен­ного тока в комплексной форме.

Современные инженерные калькуляторы в режиме «compl» позволяют выполнять все действия с комплексными числами непосредственно так же, как с обычными числами. При этом следует принять во внимание, что калькулятор выполняет действия над комплекс­ными числами только в алгебраической форме 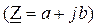и результаты расчета выдает также в алгебраической форме. Если исходные комплексные числа заданы в показательной форме 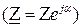, то после их ввода необходимо выполнить операцию преобразования их в алгеб­раическую форму.

Комплексный метод расчета цепей переменного тока был разработан в 1910-1912гг. американским инженером Штейнметцом и сыграл большую роль в развитии теории электри­ческих цепей переменного тока.

Мощность переменного тока

В сложной электрической цепи, состоящей из разнородных элементов R, L, C, одно­временно происходят следующие физические процессы:

а) необратимый процесс преобразования электрической энергии в дру­гие виды (теп­ловую, механическую и др.), который называется активным;

б) обратимый процесс колебания энергии между переменным электри­ческим полем конденсаторов 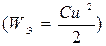, магнитным полем кату­шек 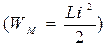и источ­ником энергии, который называется реактивным.

Процесс преобразования и процесс колебания энергии взаимно накла­дываются друг на друга, создавая в цепи единый сложный энергетический про­цесс.

Пусть электрическая цепь носит активно-индуктивный характер и может быть пред­ставлена простой схемой, состоящей из источника ЭДС е и пассив­ных элементов R и L, включенных последовательно (рис. 39):

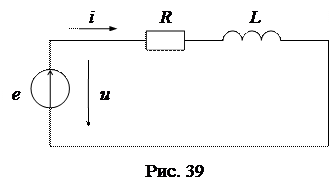Напряжение и ток на входе схемы как функции времени и их комплекс­ные изображения будут равны:

;

.

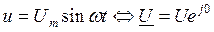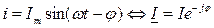Мгновенная мощность, как функция времени, состоит из двух слагае­мых:

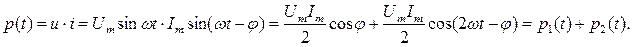
Первое слагаемое 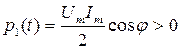характеризует процесс преоб­разования элек­трической энергии в другие виды (активный процесс). Второе слагаемое 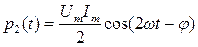изменяются по периодическому закону с частотой 2w и характери­зует процесс обмена энергией между магнитным полем приемника и источником энергии (реактивный процесс).

Количество энергии, которое преобразуется в приемнике в другие виды в единицу времени, называется активной мощностью P. Математически актив­ная мощность может быть получена как среднее значение мгновенной мощно­сти за период:

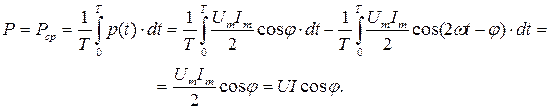
Реактивная мощность Q характеризует интенсивность обмена энергией между маг­нитным полем приемника и источником и определяется по формуле:

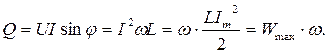
Реактивная мощность индуктивного характера 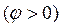положительна, а емкостного характера 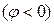отрицательна. Противоположность знаков указы­вает на тот факт, что коле­бания энергии в разнородных элементах совершаются в противофазе.

В технике используется понятие полной мощности S, которая не имеет физического смысла и определяется по формуле:

.

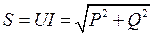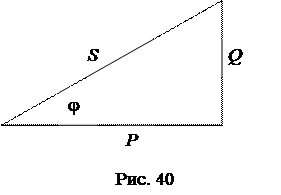
Мощности S, P, Q образуют прямоугольный треугольник, который на­зывается тре­угольником мощностей (рис. 40).

Хотя физическая размерность мощностей S, P, Q одинакова, а именно 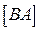, для каж­дой из них на практике применяется своя единица измерения: для активной мощности P - ватт 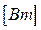, для реактивной мощности Q - вольтампер реактивный 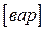, для полной мощности S - вольтампер .

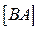В соответствии с законом сохранения энергии в цепи переменного тока должны ба­лансироваться независимо друг от друга активные и реактивные мощности приемников и ис­точников энерги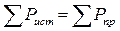и: и 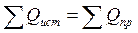. Баланс для полных мощностей не со­блюдается.

При расчете цепей переменного тока комплексным методом мощности S, P, Q пред­ставляют в комплексной форме:

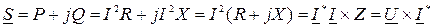
где 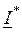- сопряженный комплекс тока .

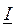Таким образом

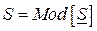- модуль комплексной мощности;

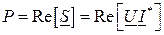- вещественная часть;

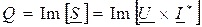- мнимая часть.