Подбор объясняющих переменных множественной линейной модели. Метод анализа матрицы коэффициентов корреляции

С формальной точки зрения, объясняющие переменные в линейной эконометрической модели должны обладать следующими свойствами:

• иметь высокую вариабельность;

• быть сильно коррелированными с объясняемой переменной;

• быть слабо коррелированными между собой;

•быть сильно коррелированными с представляемыми ими другими переменными, не используемыми в качестве объясняющих.

Объясняющие переменные подбираются с помощью статистических мето­дов. Процедура подбора переменных состоит из следующих этапов:

1. На основе накопленных знаний составляется множество так называе­мых потенциальных объясняющих переменных (первичных переменных), в которое включаются все важнейшие величины, влияющие на объясняемую переменную. Такие переменные будем обозначать X1,X2,…,Xm

2. Собирается статистическая информация о реализациях как объясняе­мой переменной, так и потенциальных объясняющих переменных. Форми­руется вектор у наблюдаемых значений переменной Y и матрица X наблю­даемых значений переменных X1,X2,…,Xm в виде

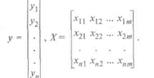
3. Исключаются потенциальные объясняющие переменные, характеризу­ющиеся слишком низким уровнем вариабельности.

4. Рассчитываются коэффициенты корреляции между всеми рассматри­ваемыми переменными.

5. Множество потенциальных объясняющих переменных редуцируется с помощью выбранной статистической процедуры.

Речь идет о том, чтобы объясняющие переменные хорошо представляли те переменные, которые не были включены в модель.

Для оценивания силы линейной зависимости объясняемой переменной Y от потенциальных объясняющих переменных X1,X2,…,Xm рассчитываются коэффициенты корреляции:

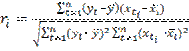(i=1,2,…,m).

Эти коэффициенты представляются в виде вектора корреляции:

Коэффициенты корреляции между потенциальными объясняющими переменными X1,X2,…,Xm рассчитываются по формуле

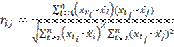(i, j = 1,2,...,m)

Образуют матрицу корреляции:

Идея этого метода сводится к выбору таких объясняющих переменных, которые сильно коррелируют с объясняемой переменной и, одновременно, слабо коррелируют между собой. В качестве исходных точек рассматриваются вектор R0 и матрица R.

Для заданного уровня значимости у и для (п — 2) степеней свободы рассчи­тывается так называемое критическое значение коэффициента корреляции:

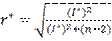, где 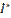— значение распределения Стьюдента для заданного у и для (п — 2) сте­пеней свободы.

Критическое значение коэф-та корреляции r* также может апри­орно задаваться аналитиком.

Процедура подбора объясняющих переменных состоит из следующих этапов:

1. Из множества потенциальных объясняющих переменных исключаются все элементы, которые удовлетворяют неравенству 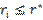поскольку они несущественно коррелируют с объясняемой переменной.

2. Из оставшихся переменных объясняющей признается такая перемен­ная Xi, для которой \r_i\ = max{\r_i\}, поскольку Xi является носителем наибольшего количества информации об объясняемой переменной.

3. Из множества потенциальных объясняющих переменных исключаются все элементы, которые удовлетворяют неравенству 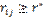поскольку эти переменные слишком сильно коррелируют с объясняющей переменной и, следовательно, только воспроизводят представляемую ею информацию.

Этапы 1—3 повторяются вплоть до момента опустошения множества по­тенциальных объясняющих переменных.

43. Подбор переменных в модели множественной регрессии на основе метода оценки информационной ёмкости.

С формальной точки зрения, объясняющие переменные в линейной эконометрической модели должны обладать следующими свойствами:

• иметь высокую вариабельность;

• быть сильно коррелированными с объясняемой переменной;

• быть слабо коррелированными между собой;

•быть сильно коррелированными с представляемыми ими другими переменными, не используемыми в качестве объясняющих.

Объясняющие переменные подбираются с помощью стат-ких мето­дов. Процедура подбора переменных состоит из следующих этапов:

1. На основе накопленных знаний составляется множество так называе­мых потенциальных объясняющих переменных (первичных переменных), в которое включаются все важнейшие величины, влияющие на объясняемую переменную. Такие переменные будем обозначать X1,X2,…,Xm

2. Собирается статистическая информация о реализациях как объясняе­мой переменной, так и потенциальных объясняющих переменных. Форми­руется вектор у наблюдаемых значений переменной Y и матрица X наблю­даемых значений переменных X1,X2,…,Xm в виде

3. Исключаются потенциальные объясняющие переменные, характеризу­ющиеся слишком низким уровнем вариабельности.

4. Рассчитываются коэффициенты корреляции между всеми рассматри­ваемыми переменными.

5. Множество потенциальных объясняющих переменных редуцируется с помощью выбранной статистической процедуры.

Речь идет о том, чтобы объясняющие переменные хорошо представляли те переменные, кот не были включены в модель.

Идея метода показателей информационной емкости сводится к выбору таких объясняющих переменных, которые сильно коррелированы с объясня­емой переменной, и одновременно, слабо коррелированы между собой. В ка­честве исходных точек этого метода рассматриваются вектор R0 и матрица R.

Рассматриваются все комбинации потенциальных объясняющих пере­менных, общее количество которых составляет I = 2^W-1. Для каждой комбинации потенциальных объясняющих переменных рас­считываются индивидуальные и интегральные показатели информацион­ной емкости.

Индивидуальные показатели информационной емкости в рамках конк­ретной комбинации рассчитываются по формуле

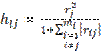; (l=1,2,…,L; j=1,2,… 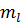), где l – номер переменной, 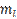– количество переменных в рассматриваемой комбинации.

Интегральные показатели информационной емкости потенциальных объясняющих переменных рассчитываются по формуле

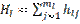, (l=1,2,…,L).

Индивидуальные у интегральные показатели информационной емкости нормируются в интервале [0; 1]. Их значения оказываются тем больше чем сильнее объясняющие переменные коррелируют с объясняемой переменной и чем слабее они коррелируют между собой.

В качестве объясняющих выбирается такая комбинация переменных, которой соответствует максимальное значение интегрального показателя и формационной емкости.