Множества, подмножества и способы их задания.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЯЗАНСКОЙ ОБЛАСТИ
ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РЯЗАНСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖ»
Цикловая методическая комиссия естественно-математических дисциплин
Н.А. Ивина
Математика
Учебно-методическое пособие для студентов, обучающихся по заочной форме обучения по специальностям среднего профессионального образования
Товароведение и экспертиза качества потребительских товаров
Экономика и бухгалтерский учет (по отраслям)
Рязань 2014
| Согласовано на заседании ЦМК естественно-математических дисциплин Протокол № _______ «____» __________ 20___ г. Председатель цикловой комиссии ________________ Ю.Б. Щенева | Утверждено Заместитель директора по учебной работе «____»________ 20___ г. _________ Н.В. Чекурова |
Учебно-методическое пособие по дисциплине Математика разработано на основе Федерального государственного образовательного стандарта (ФГОС) по специальностям среднего профессионального образования 100801(38.02.05) Товароведение и экспертиза качества потребительских товаров, 080114(38.02.01) Экономика и бухгалтерский учет(по отраслям).
| Составитель: | Н.А. Ивина, преподаватель высшей квалификационной категории ОГБОУ СПО «Рязанский технологический колледж» |
| Рецензенты: | Ю.Б. Щенева, магистр математики, преподаватель высшей квалификационной категории ОГБОУ СПО «Рязанский технологический колледж» |
Технический исполнитель: Ю.В. Попова
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ | |
| ТЕМАТИЧЕСКИЙ ПЛАН И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ «МАТЕМАТИКА» | |
| КУРС ЛЕКЦИЙ | |
| Раздел 1 Теория множеств | |
| Раздел 2 Линейная алгебра | |
| Раздел 3 Теория пределов | |
| Раздел 4 Дифференциальное исчисление функций одной переменной | |
| Раздел 5 Интегральное исчисление функций одной переменной | |
| Раздел 6 Теория вероятностей | |
| МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ | |
| ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ | |
| ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ВОПРОСОВ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА» | |
| ЛИТЕРАТУРА |
ВВЕДЕНИЕ
Учебно-методическое пособиеучебной дисциплины «Математика» разработано на основе Федерального государственного образовательного стандарта по специальностям 100801(38.02.05) Товароведение и экспертиза качества потребительских товаров, 080114(38.02.01) Экономика и бухгалтерский учет(по отраслям) в соответствии с утвержденным учебным планом и содержит методические указания и контрольные задания по основным темам дисциплины.
По каждой теме дано краткое изложение основных теоретических сведений и приведены примеры решения типовых задач, что способствует самостоятельному изучению материала и выполнению контрольных заданий.
В результате освоения учебной дисциплины студент должен уметь:
решать прикладные задачи в области профессиональной деятельности;
В результате освоения учебной дисциплины студент должен знать:
значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы;
основные математические методы решения прикладных задач в области профессиональной деятельности;
основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики; основы интегрального и дифференциального исчисления.
Программа рассчитана на 20 часов.
Учебным планом предусмотрено проведение обзорных и установочных занятий в период лабораторно-экзаменационной сессии. Студенты выполняют домашнюю контрольную работу.
Основным видом итогового контроля является экзамен, проводимый после изучения полного курса дисциплины.
К экзамену допускаются студенты, выполнившие контрольную работу и получившие положительную оценку.
Критерии оценки знаний и умений на экзамене:
Процент результативности (правильных ответов):
100 - 85% - «отлично»
84 - 70% - «хорошо»
69 - 55% - «удовлетворительно»
ТЕМАТИЧЕСКИЙ ПЛАН И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ «МАТЕМАТИКА»
| Наименование разделов | Содержание учебного материала, самостоятельная работа обучающихся | Объем часов |
| Раздел 1. Теория множеств | Тема 1.1. Основные понятия теории множеств. | |
| Самостоятельная работа | ||
| Понятие множества. Конечные и бесконечные множества, пустое множество. Подмножество. Способы задания множеств. Теоретико-множественные диаграммы. Операции над множествами и их свойства. | ||
| Раздел 2. Элементы линейной алгебры | Тема 2.1. Основы линейной алгебры | |
| Самостоятельная работа | ||
| Понятие матрицы. Действия над матрицами, их свойства. | ||
| Определители 2-го и 3-го порядка, вычисление определителей. | ||
| Определители n-го порядка, свойства определителей. Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца. | ||
| Обратная матрица. Ранг матрицы. Элементарные преобразования матрицы. Ступенчатый вид матрицы. | ||
| Исследование и решение систем линейных алгебраических уравнений методом Гаусса. Решение систем линейных алгебраических уравнений методом Крамера, матричным методом. | ||
| Практические занятия Операции над матрицами. Вычисление определителей. Нахождение обратной матрицы. Вычисление ранга матрицы. Решение систем линейных уравнений методом Гаусса. Решение систем линейных уравнений методом Крамера, матричным методом. | ||
| Раздел 3. Введение в математический анализ | Тема 3.1. Теория пределов | |
| Самостоятельная работа | ||
| Числовые последовательности. Монотонные, ограниченные последовательности. Предел последовательности, свойства предела. Бесконечно малые и бесконечно большие последовательности, связь между ними, символические равенства. Предел суммы, произведения, частного двух последовательностей. Признак сходимости монотонной последовательности. | ||
| Предел функции. Основные теоремы о пределах (суммы, произведения, частного). | ||
| Первый и второй замечательные пределы. | ||
Практические занятия Раскрытие неопределенностей, 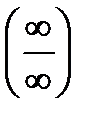 ,  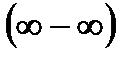,  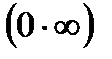. Вычисление пределов функций с помощью замечательных. | ||
| Тема 3.2. Непрерывность функции | ||
| Самостоятельная работа | ||
| Непрерывность функции. Точки разрыва функции и их классификация. Непрерывность функции на отрезке | ||
| Раздел 4. Дифференциальное исчисление функции одной переменной | Тема 4.1. Производная функции. | |
| Производная функции, её геометрический, механический смысл, свойства. | ||
| Производная сложной функции. Таблица производных. Правила дифференцирования. Дифференциал функции. Его геометрический смысл. Производные и дифференциалы высших порядков. Раскрытие неопределенностей, правило Лопиталя. | ||
| Тема 4.2. Исследование функций. Построение графиков функций | ||
| Самостоятельная работа | ||
| Исследование функций. Точки экстремума. Необходимые и достаточные условия максимума и минимума. | ||
| Выпуклость и вогнутость. Асимптоты кривых. | ||
| Общая схема исследования и построения графиков. | ||
| Раздел 5. Основы интегрального исчисления | Тема 5.1. Понятие неопределенного интеграла | |
| Самостоятельная работа | ||
| Задачи, приводящие к понятию неопределённого интеграла. Первообразная, неопределенный интеграл, его свойства. Таблица интегралов. Непосредственное интегрирование. | ||
| Интегрирование методом замены переменной. Интегрирование по частям. | ||
| Тема 5.2. Понятие определенного интеграла. | ||
| Самостоятельная работа | ||
| Задачи, приводящие к понятию определённого интеграла. Формулировка теоремы о его существовании. Свойства. | ||
| Теорема о среднем. Формула Ньютона-Лейбница. Вычисление определённого интеграла с помощью интегрирования по частям и замены переменной. | ||
| Тема 5.3. Приложение определенного интеграла | ||
| Самостоятельная работа | ||
| Приложение определенного интеграла в геометрии | ||
| Раздел 6. Основы теории вероятностей и математической статистики | Тема 6.1. Случайные события. Относительная и условная вероятность. Полная вероятность | |
| Самостоятельная работа | ||
| Случайные события. Относительная частота и вероятность. Основные свойства вероятностей. | ||
| Правило сложения вероятностей. Условные вероятности, правило умножения. Формула полной вероятности. | ||
| Тема 6.2. Элементы математической статистики. | ||
| Самостоятельная работа | ||
| Понятие о задачах математической статистики. Функции выборки. Некоторые важнейшие распределения. Методы оценки параметров распределений. Генеральная совокупность и выборка. Выборочное среднее и выборочные дисперсии. Типовые выборочные распределения. | ||
| Раздел 7. Основы теории комплексных чисел | Тема 7.1. Теория комплексных чисел | |
| Самостоятельная работа | ||
| Определение комплексных чисел в алгебраической форме, действия над ними. Геометрическое изображение комплексных чисел. Решение алгебраических уравнений. Тригонометрическая форма комплексных чисел. Переход от алгебраической формы к тригонометрической и обратно. Действия над комплексными числами в тригонометрической форме. Показательная форма комплексных чисел, действия над ними. Тождество Эйлера. | ||
| Итого | ||
| В том числе обязательная аудиторная нагрузка |
КУРС ЛЕКЦИЙ
РАЗДЕЛ 1. Теория множеств
Множества, подмножества и способы их задания.
Понятие множества является одним из тех фундаментальных понятий математики, которым трудно дать четкое определение, используя элементарные понятия. Множество — это совокупность, набор, собрание элементов, объединяемых по какому-либо признаку. Родоначальник теории множеств Георг Кантор (1845 - 1918) определял множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью».
Можно говорить о множестве присутствующих в данной аудитории, множестве букв русского алфавита, множество целых чисел, множество планет Солнечной системы и т.п. При этом о множестве можно вести речь только тогда, когда элементы множества различимы между собой. Например, нельзя говорить о множестве капель в стакане воды, так как невозможно четко и ясно указать каждую отдельную каплю. Объекты, составляющие множество, называются его элементами.
Общим обозначением множества служит пара фигурных скобок { }, внутри которых перечисляются элементы множества. Для обозначения конкретных множеств используются различные прописные буквы алфавита (обычно латинского) с индексами или без них. Для обозначения элементов множества в общем виде используются различные строчные буквы алфавита с индексами или без них. Если объект а является элементом множества А, то этот факт записывается так: а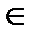 
А, в противном случае пишут а 
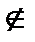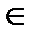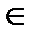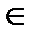А. Символ является символом принадлежности объекта множеству. Вместо записи а А, в А, с 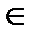А может быть использована запись а, в, с 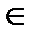А.
Множество, содержащее конечное число элементов, называется конечным, в противном случае оно называется бесконечным.
В дальнейшем мы будем рассматривать числовые множества, элементы которых - действительные (вещественные) числа.
Геометрически множество действительных чисел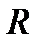 
изображается точками числовой прямой (или числовой оси), то есть прямой, на которой выбрано начало отсчета, положительное направление и единица масштаба. Между множеством действительных чисел и точками числовой прямой существует взаимно однозначное соответствие, то есть каждому действительному числу соответствует определенная точка числовой прямой, и, наоборот, каждой точке прямой- определенное действительное число.
Множество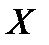 
, элементы которого удовлетворяют неравенству 
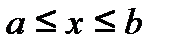, называется отрезком 
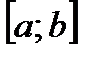; неравенству 
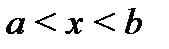- интервалом 
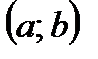; неравенствам 
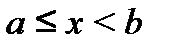или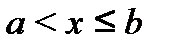 
, называются полуинтервалами соответственно 
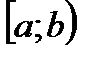и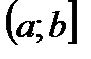 
. Наряду этими рассматриваются бесконечные интервалы и полуинтервалы 
, 
, 
, 
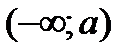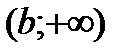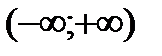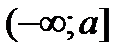и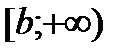 
. В дальнейшем все указанные множества мы объединяем термином промежуток 
.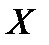