Загальне рівняння другого порядку з двома змінними
КРИВІ ДРУГОГО ПОРЯДКУ НА ПЛОЩИНІ
До кривих другого порядку належить такі лінії:коло, еліпс, гіпербола, парабола, рівняння яких у декартовій прямокутній системі координат є рівняння другого ступеня відносно 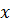 і
і 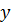 . Криві другого порядку називають ще конічними перерізами, оскільки їх можна дістати як лінії перетину прямого кругового конуса площинами.
. Криві другого порядку називають ще конічними перерізами, оскільки їх можна дістати як лінії перетину прямого кругового конуса площинами.
Дійсно:
- Якщо площина перетинає конічну поверхню перпендикулярно осі обертання, то в перетині утворюється коло, якщо площина проходить через вершину конуса, то в результаті утворюється точка, тобто вироджене коло.
- Якщо площина перетинає тільки одну частину конічної поверхні і не паралельна жодній твірній, то в перетині буде еліпс (рис.1а).
- Якщо площина перетинає одну частину конічної поверхні і паралельна одній твірній, то в перетині буде парабола, якщо площина проходить через вершину і одну з твірних, то в перетині буде пряма,тобто вироджена парабола(рис.1б).
- Якщо площина перетинає дві частини конічної поверхні і паралельна осі конічної поверхні, то в перетині буде гіпербола, якщо січна площина проходить через вершину конуса і перетинає дві його частини, то в перетині буде пара прямих, що перетинаються, тобто виродженою гіперболою(рис.1в).
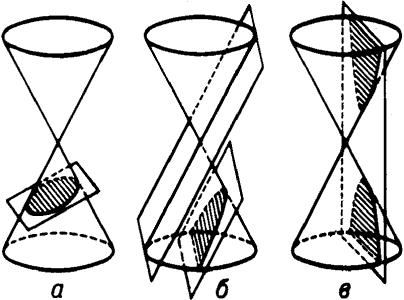
Рис. 1
Коло
Колом називають геометричне місце точок (ГМТ), рівновіддалених від фіксованої точки – центра кола.
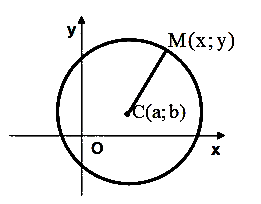 Канонічне рівняння кола:
Канонічне рівняння кола:
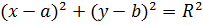 .
.
Наприклад, рівняння
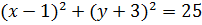 ,
,
є рівнянням кола радіуса 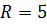 з центром в точці
з центром в точці 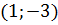 .
.
Якщо центр кола збігається з початком координат, то рівняння кола набирає вигляд
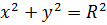 .
.
Приклад 1.Скласти рівняння кола радіуса 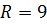 з центром у точці
з центром у точці 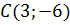 .
.
Розв’язання:
Підставивши значення координат точки 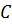 і значення радіуса в рівняння кола, матимемо
і значення радіуса в рівняння кола, матимемо 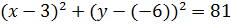 , або
, або
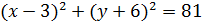 .
.
Приклад 2. Довести, що рівняння 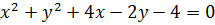 є рівнянням кола. Знайти його центр і радіус.
є рівнянням кола. Знайти його центр і радіус.
Розв’язання:
Перетворимо ліву частину заданого рівняння:
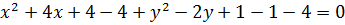 .
.
Звідси
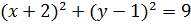 .
.
Це рівняння є рівнянням кола з центром у точці 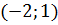 , радіус кола дорівнює
, радіус кола дорівнює 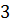 .
.
Еліпс
Еліпсом називається геометричне місце точок, сума відстаней яких до двох заданих точок (фокусів) дорівнює постійній величині 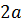 (сума фокальних радіусів
(сума фокальних радіусів 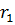 та
та 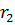 дорівнює великій півосі еліпса).
дорівнює великій півосі еліпса).
Канонічне рівняння еліпса
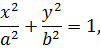
де параметри рівняння 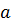 та
та  дорівнюють півосям еліпса, що розташовані на осях координат
дорівнюють півосям еліпса, що розташовані на осях координат 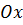 та
та 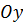 відповідно
відповідно
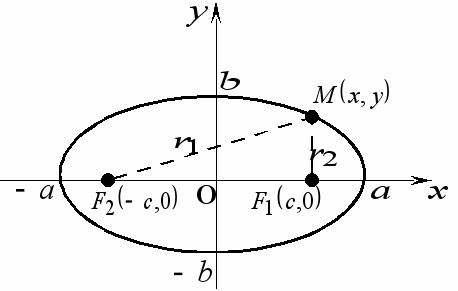
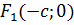 та
та 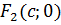 - лівий та правий фокуси еліпса,
- лівий та правий фокуси еліпса,
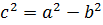 , де
, де 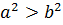 ,
,
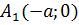 ,
, 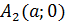 ,
, 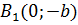 ,
, 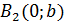 - вершини еліпса,
- вершини еліпса,
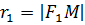 ,
, 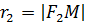 - фокальні радіуси,
- фокальні радіуси, 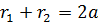 ,
,
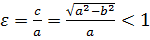 – ексцентриситет – міра відхилення еліпса від кола,
– ексцентриситет – міра відхилення еліпса від кола,
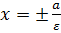 - рівняння директрис.
- рівняння директрис.
Зауваження:
Якщо центр еліпса перенесено в точку 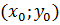 , то рівняння має вигляд
, то рівняння має вигляд
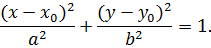
Приклад 3.Скласти канонічне рівняння еліпса, який проходить через точку 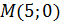 , якщо фокальна відстань дорівнює
, якщо фокальна відстань дорівнює 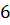 .
.
Розв’язання:
Оскільки фокальна відстань дорівнює 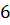 , то
, то 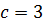 . Запишемо рівняння еліпса
. Запишемо рівняння еліпса
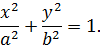
За умовою задачі точка 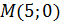 належить еліпсу, отже
належить еліпсу, отже
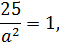
звідси 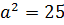 . Знайдемо
. Знайдемо 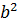 ,
, 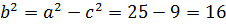 .
.
Отже, шуканим рівнянням еліпса є рівняння
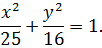
Приклад 4.Довести, що рівняння 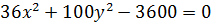 є рівнянням еліпса, знайти координати фокусів і фокальну відстань.
є рівнянням еліпса, знайти координати фокусів і фокальну відстань.
Розв’язання:
Розділивши обидві частини рівняння на 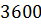 , дістанемо
, дістанемо
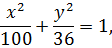
це є рівнянням еліпса.
З рівняння 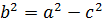 випливає, що
випливає, що 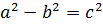 . Оскільки
. Оскільки 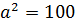 ,
, 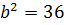 ,
, 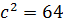 , звідси
, звідси 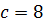 . Фокуси еліпса знаходяться в точках
. Фокуси еліпса знаходяться в точках 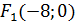 і
і 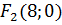 . Фокальна відстань
. Фокальна відстань 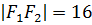 .
.
Гіпербола
Гіперболою називається геометричне місце точок, модуль різниці відстаней яких до двох заданих точок (фокусів) дорівнює постійній величині 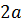 .
.
Канонічне рівняння гіперболи
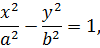
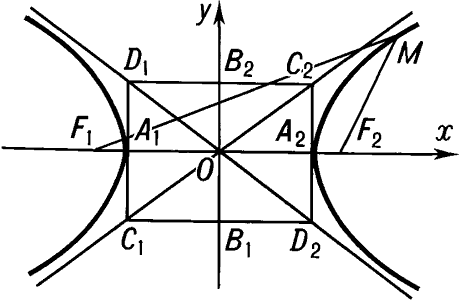
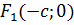 та
та 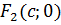 - лівий та правий фокуси гіперболи,
- лівий та правий фокуси гіперболи,
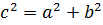 ,
,
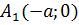 ,
, 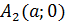 - вершини еліпса,
- вершини еліпса,
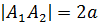 ,
, 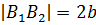 - дійсна і уявна осі,
- дійсна і уявна осі,
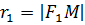 ,
, 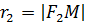 - фокальні радіуси,
- фокальні радіуси,
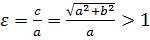 – ексцентриситет,
– ексцентриситет,
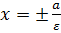 - рівняння директрис.
- рівняння директрис.
Зауваження:
Якщо центр гіперболи перенесено в точку 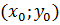 , то рівняння має вигляд
, то рівняння має вигляд
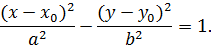
Приклад 5.Записати канонічне рівняння гіперболи, яка проходить через точку 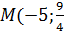 ), якщо фокальна відстань гіперболи дорівнює
), якщо фокальна відстань гіперболи дорівнює 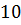 .
.
Розв’язання:
Оскільки 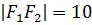 , то
, то 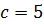 . Запишемо канонічне рівняння гіперболи
. Запишемо канонічне рівняння гіперболи
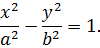
За умовою точка належить гіперболі, отже:
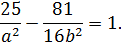
З другого рівняння дістанемо співвідношення для визначення 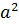 і
і 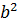 :
:
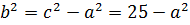 .
.
Розв’язавши систему:
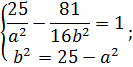
знайдемо 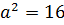 ,
, 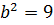 . Шуканим рівнянням є рівняння
. Шуканим рівнянням є рівняння
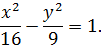
Приклад 6. Довести, що рівняння 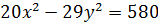 є рівнянням гіперболи. Знайти координати фокусів.
є рівнянням гіперболи. Знайти координати фокусів.
Розв’язання:
Розділивши обидві частини рівняння на 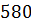 , дістанемо
, дістанемо
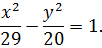
Це є рівнянням гіперболи, для якої 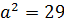 ,
, 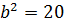 . Із співвідношення
. Із співвідношення 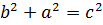 знаходимо
знаходимо 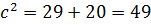 ,
, 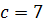 . Отже, фокуси гіперболи знаходяться в точках
. Отже, фокуси гіперболи знаходяться в точках 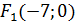 і
і 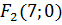 .
.
Парабола
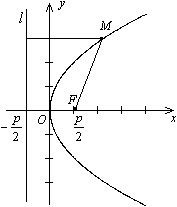 Параболою називається геометричне місце точок, відстань яких до заданої прямої (директриси) та заданої точки (фокуса) рівні.
Параболою називається геометричне місце точок, відстань яких до заданої прямої (директриси) та заданої точки (фокуса) рівні.
Канонічне рівняння гіперболи
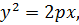
де 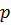 - відстань між фокусом
- відстань між фокусом 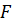 та директрисою,
та директрисою,
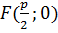 – фокус,
– фокус,
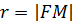 - фокальний радіус,
- фокальний радіус,
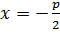 – рівняння директриси,
– рівняння директриси,
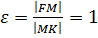 - ексцентриситет.
- ексцентриситет.
Зауваження:
Якщо центр параболи перенесено в точку 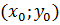 , то рівняння має вигляд
, то рівняння має вигляд
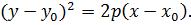
Приклад 7.Скласти канонічне рівняння параболи, якщо парабола симетрична відносно осі 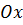 і проходить через точку
і проходить через точку 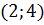 .
.
Розв’язання:
Оскільки парабола симетрична відносно осі 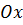 , то задається рівнянням
, то задається рівнянням 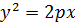 . Точка
. Точка 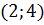 належить параболі, то
належить параболі, то 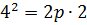 , звідси
, звідси 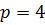 .
.
Отже, рівняння параболи 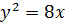 .
.
Загальне рівняння другого порядку з двома змінними
Загальне рівняння другого порядку з двома змінними має вигляд
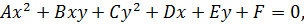
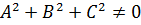 .
.
Для визначення типу кривої треба звести це рівняння до одного з канонічних рівнянь кривих ліній другого порядку шляхом виділення повних квадратів.
Потрібно мати на увазі:
1. Якщо коефіцієнти 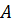 та
та 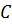 одного знаку і рівні, то це рівняння кола.
одного знаку і рівні, то це рівняння кола.
2. Якщо коефіцієнти 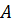 та
та 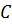 одного знаку, але не рівні - рівняння еліпса.
одного знаку, але не рівні - рівняння еліпса.
3. Якщо 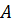 та
та 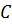 різних знаків - рівняння гіперболи.
різних знаків - рівняння гіперболи.
4. Якщо 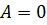 або
або 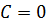 – рівняння параболи.
– рівняння параболи.
Завдання для самоконтролю
1. Скласти рівняння кола:
1) з центром у початку координат і радіусом 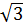 ;
;
2) з центром у точці 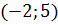 і радіусом
і радіусом 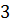 .
.
2. Скласти канонічне рівняння еліпса, якщо відомо:
1) відстань між фокусами дорівнює 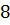 , а мала вісь
, а мала вісь 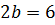 ;
;
2) дві його вершини знаходяться в точках 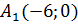 і
і 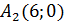 , а фокуси
, а фокуси 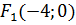 і
і 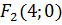 ;
;
3) дві його вершини знаходяться в точках 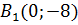 і
і 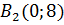 , а фокуси
, а фокуси 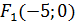 і
і 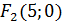 ;
;
4) велика вісь 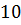 , а ексцентриситет
, а ексцентриситет 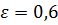 .
.
3. Скласти канонічне рівняння гіперболи, якщо відомі:
1) координати її вершин 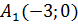 і
і 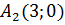 та координати фокусів
та координати фокусів 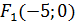 і
і 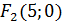 ;
;
2) координати її вершин 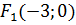 і
і 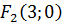 та координати фокусів
та координати фокусів 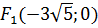 і
і 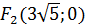 ;
;
3) відстань між фокусами 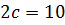 , а між вершинами
, а між вершинами 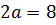 ;
;
4) дійсна піввісь 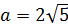 , а ексцентриситет
, а ексцентриситет 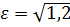 ;
;
5) відстань між фокусами 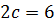 , а ексцентриситет
, а ексцентриситет 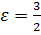 ;
;
6) уявна вісь 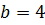 , а відстань між фокусами
, а відстань між фокусами 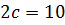 .
.
4. Скласти канонічне рівняння параболи, вершина якої знаходиться у початку координат, якщо відомо:
1) парабола розташована у правій півплощині симетрично відносно осі 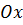 і її параметр
і її параметр 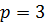 ;
;
2) парабола розташована у лівій півплощині симетрично відносно осі 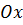 і її параметр
і її параметр 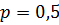 ;
;
3) парабола розташована у верхній півплощині симетрично відносно осі 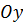 і її параметр
і її параметр 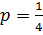 ;
;
4) парабола симетрична відносно осі 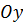 і проходить через точку
і проходить через точку 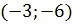 .
.
5. Побудувати криві другого порядку, задані канонічними рівняннями:
1) 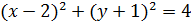 ;
;
2) 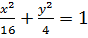 ;
;
3) 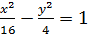 ;
;
4) 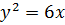 .
.
6. Визначити тип кривої
1) 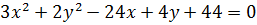 ;
;
2) 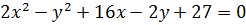 ;
;
3) 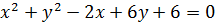 ;
;
4) 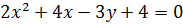 ;
;
5) 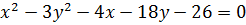 ;
;
6) 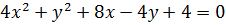 ;
;
7) 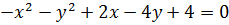 ;
;
8) 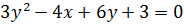 .
.
7. Земля рухається по еліптичній орбіті, в одному з фокусів якої знаходиться Сонце. Обчислити ексцентриситет земної орбіти, якщо найближча до Сонця точка земної орбіти (перигелій) знаходиться на відстані 147 млн. км від Сонця, а найбільш віддалена від Сонця точка (афелій ) знаходиться на відстані 152 млн. км нього.
8. Ексцентриситет траєкторії руху першої радянської космічної ракети, запущеної в бік Місяця 2 січня 1959 р., дорівнює 1,05. Визначити вид траєкторії ракети.
