Статистический смысл энтропии
Из (2.67)
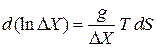
и (2.68)
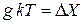
находим
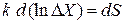 , (2.70)
, (2.70)
\Интегрируем (2.70)
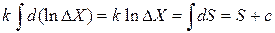 .
.
Выбираем 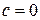 , тогда система в одном микросостоянии
, тогда система в одном микросостоянии 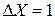 имеет нулевую энтропию в соответствии с третьим началом термодинамики. В результате
имеет нулевую энтропию в соответствии с третьим началом термодинамики. В результате
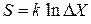 , (2.71)
, (2.71)
Выражение (2.71) определяет статистический смысл энтропии – энтропия пропорциональна логарифму числа микросостояний фазового ансамбля.
Фазовый объем системы, состоящей из независимых подсистем 1 и 2, равен произведению объемов, которые они занимают:
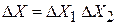 .
.
Из (2.71) получаем аддитивность энтропии
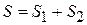 (2.72)
(2.72)
– энтропия системы равна сумме энтропий независимых подсистем.
Из (2.20)
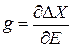
и (2.70)
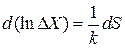
находим
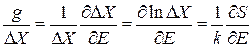 .
.
Используем (2.68)
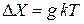 ,
,
получаем
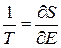 . (2.73)
. (2.73)
Из приведенных соотношений следует:
1.Согласно (2.71)
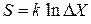
выполняется
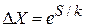 , (2.74)
, (2.74)
число микросостояний системы увеличивается экспоненциально с ростом энтропии.
2. Чем больше возможных микросостояний, реализующих макросостояние, тем меньше информации о системе. Увеличение энтропии означает уменьшение информации о системе и увеличение ее хаотичности. Чем более упорядочена система, тем меньше ее энтропия. Для контроля и управления системой необходимо снижать ее энтропию.
3. Согласно (2.73) чем ниже температура, тем быстрее уменьшается энтропия с понижением энергии системы. Для уменьшения энтропии следует снижать температуру и использовать переходы с малой энергией. Согласно теореме Нернста, или третьему началу термодинамики, при 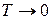 у любой системы
у любой системы 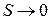 и она занимает лишь одно микросостояние.
и она занимает лишь одно микросостояние.
4. Для замкнутого обратимого процесса выполняется равенство Клаузиуса
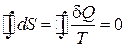 ,
,
или второе начало термодинамики. Следовательно, энтропия является функцией состояния.
