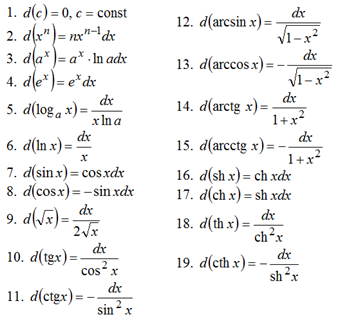Вопрос. Частные производные и дифференциалы функции нескольких переменных высших порядков.

Примеры.

Частные производные высших порядков

Производные n-го порядка от основных элементарных функцийСправедливы формулы

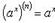
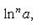
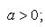
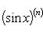
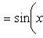
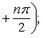
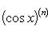
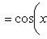
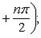
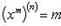
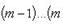
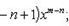
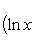
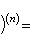
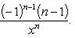
Формула Лейбница

Если u и v - n-кратно дифференцируемые функции, то

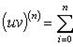
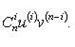
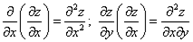
- производные от

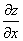
по x и y.

Эти же производные можно записать и в другой форме:

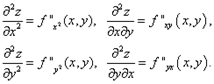
Все эти производные являются частными производными второго порядка от функции f(x, y). От них можно опять взять производные. Например,

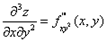
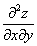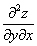Пример 7. Найти частные производные и функции 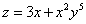и убедиться в равенстве этих частных производных.

Решение:

;

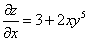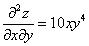
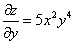
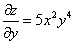
Как видно из решения, смешанные частные производные равны.

Пример 8. Для функции

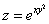
вычислить частную производную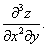

Решение. Первое и второе дифференцирование производим по x:

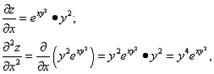
а третье – по y:

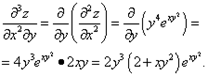
Производные и дифференциалы высших порядков

Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производнойфункции f и обозначается f". Таким образом,

f"(x) = (f'(x))'.

Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f⁽ⁿ⁾. Итак,

f⁽ⁿ⁾(x) = (f^(n-1)(x))', n ϵ N, f⁽⁰⁾(x) = f(x).

Число n называется порядком производной.

Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,

dⁿf(x) = d(d^n-1f(x)), d⁰f(x) = f(x), n ϵ N.

Если x - независимая переменная, то dx = const и d²x = d³x = ... = dⁿx = 0

.

В этом случае справедлива формула

dⁿf(x) = f⁽ⁿ⁾(x)(dx)ⁿ.

Вопрос. Дифференциал сложной функции нескольких переменных. Инвариантность формы записи дифференциала.

Дифференцирование сложной функции.

Теорема: Пусть 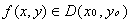и функции x = x(u, v)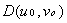 , y(u, v)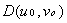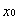 = x(u₀, v₀), y₀ = y(u₀, v₀).

Тогда f(x(u, v), y(u, v))D(u₀, v₀) и

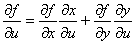
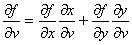
Доказательство:Рассмотрим разности:

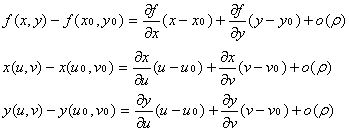
из которых следует, что

f(x(u, v), y(u, v)) - f(x(u₀, v₀), y(u₀, v₀)) =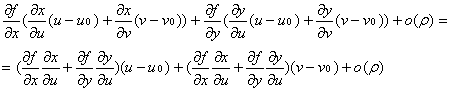

Следовательно, по определению дифференцируемости функция двух переменных:

f(x(u, v), y(u, v))D(u₀, v₀) и

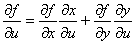
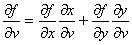
Теорема доказана.

Дифференциал функции двух переменных. Свойство инвариантности дифференциала.

Пусть .

Определение: Дифференциал d 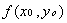функции 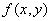в точке 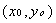называется следующее выражение:

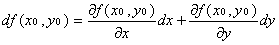
или сокращённо: 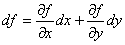, где dx и dy – дифференциалы переменных x и y.

Пусть x = x(u, v)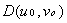 и y(u, v) .

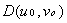Тогда по определению:

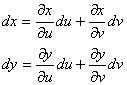
Следовательно, мы можем представить df в следующем виде:

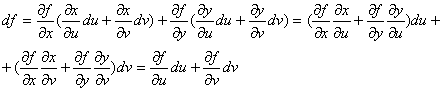
Последнее равенство следует из доказанных формул замены переменных.

Таким образом df можно представить в виде:

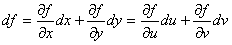
Это равенство и выражает свойство инвариантности первого дифференциала.

Первые частные производные 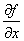и 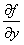есть функции от переменных x и y. Назовём по определению вторыми частными производными функции 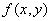следующие выражения:

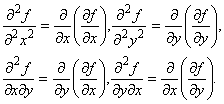
Пример:

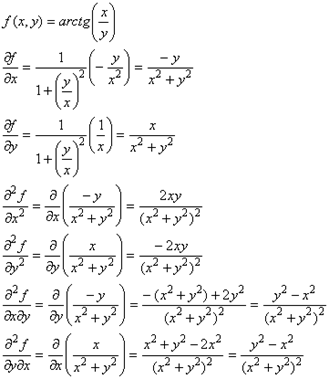
Заметим, что 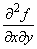= 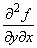. Это свойство обобщается следующей теоремой.

Теорема: Пусть 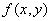, 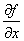и 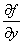непрерывны в некоторой окрестности точки (x, y), а 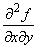и 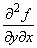непрерывны в самой точке (x, y). Тогда в точке (x, y) равенство:

=

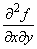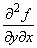
Инвариантность формул первого дифференциала

Пусть существует сложная функция 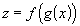, и существует ее производная: 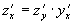. Считая y независимой переменной, получим формулу дифференциала: 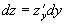. Теперь, если считать y зависимой от x, получим: 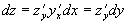, т.к. 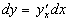. То есть получается, что формула дифференциала не зависит от типа переменной.

Не взирая на то, является ли переменная x зависимой или нет, для вычисления дифференциала используется единая формула - инвариантность формул.

Таблица дифференциалов