Разминка на «понимание» движения

Классы

Модуль 1. Задачи на движение

Из пункта А и пункта ВВышли навстречу два пешехода.От пункта A до пункта ВДорога только одна.Идут они с нормальной скоростью,Кругом хорошая погода.Вопрос: встретятся они, или нет?Ответ: по-видимому, да.Нет. Да. Да. Нет. Да.Юлий Ким. Песня о двух пешеходах.

Учителю. Мы не излагаем теорию решения задач «на движение», а лишь заостряем Ваше внимание на некоторых аспектах решения задач такого типа.

Для начала с учащимися надо повторить известные единицы измерения расстояния (пройденного пути), времени и скорости.

Кроме обычных единиц измерения расстояния метрической системы мер: километр, метр, сантиметр и т.д., можно познакомить учащихся с другими единицами измерения.

Например, раньше в России использовались такие меры:

1 сажень = 213,36 см

1 аршин = 71,12 см

1 фут = 12 дюймов

1 вершок = 1 ¾ дюйма

1 верста = 500 саженей

1 дюйм = 2,54 см

В настоящее время в англо-американской системе мер используются сухопутная миля, равная 1 609 м, и морская миля, равная 1852 м. Эта морская миля принята всеми странами, как единица расстояния на воздушном и морском транспорте.

Учителю. Особое внимание уделите переводу скоростей из одной системы мер в другую, как наиболее сложному.

Задача 1. (ЧИП -2010) Средняя скорость движения Земли по орбите вокруг Солнца

(А) 30 км/мин; (Б) 30 м/с; (В) 30 км/ч; (Г) 30 км/с; (Д) 30 м/мин.

Решение.

(А) 30 км/мин - значит 30 километров за минуту, это скорость сверхзвукового самолета Конкорд, можно перевести в привычные 1800 км/час.

(Б) 30 м/с = 1800 м/мин = 108000 м/ч = 108 км/ч – это скорость машины по хорошей дороге.

(В) 30 км/ч - это скорость машины по разбитой дороге;.

(Г) 30 км/с -скорость движения Земли по орбите вокруг Солнца.

(Д) 30 м/мин – это скорость идущего человека.

Ответ:(Г) 30 км/сек.

Задача 2. (Кенгуру-2006)Длина крокодила от головы до хвоста равна 4,5 метра, а от хвоста до головы – 24 пяди. Это означает, что одна пядь

(А) меньше 15 см (B) больше 15, но меньше 16 см (C) больше 17, но меньше 18 см

(D) больше 18, но меньше 19 см (E) больше 20 см

Решение. Найдем, сколько метров составляет 1 пядь:

4,5 : 24= 0, 1875 (м) = 18,75 (см).

Ответ: (D) больше 18, но меньше 19 см.

При решении задач на равномерное движение по прямой принимаются обычно следующие допущения:

1. Движение на отдельных участках считается равномерным, а пройденный путь Sопределяется по формуле: S = v·t,где t - время, v – скорость.

2. Скорость, время движения и пройденный путь, как и в реальной жизни, считаются положительными.

3. Повороты движущихся тел принимаются мгновенными, то есть, происходят без затрат времени; скорость при этом тоже меняется мгновенно.

Учителю. Повторите с ребятами, как находится скорость, если известны расстояние и время, и как находится время, если известны расстояние и скорость.

Задача 3. Велосипедист поднимался на холм со скоростью 15 км/ч, а спустился он с холма тем же путем со скоростью 24 км/ч, потратив на спуск на 9 мин меньше, чем на подъем. Чему равна длина дороги, ведущей на холм?

Решение.1 способ.Пусть х км – длина дороги. Тогда на подъем велосипедист затратил 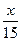часов, а на спуск – 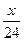часа. По условию: 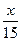– 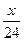= 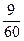. Отсюда находим: х = 6.

2 способ. Обозначим за х время подъема и заполним таблицу.

	v (км/ч)	t (час)	S (км)
Подъем на холм		х	15х
Спуск с холма		х -	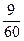24 (х - )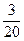

Так как путь на холм и с холма одинаков, составляем уравнение: 15х = 24(х - 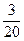). Решив уравнение, получим: х = 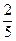. Значит, длина дороги 6 км.

Ответ: 6 км.

Хорошие задачи на движение можно найти в заданиях международного конкурса Кенгуру, например:

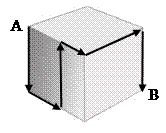Задача 4. (К-2005)Муравей ползет по поверхности кубика из точки А в точку В по пути, отмеченному стрелками. Чему равна длина этого пути, если ребро кубика равно 12 см?

(A) 36 см (B) 48 см (C) 50 см (D) 60 см

(E) невозможно определить

Решение.Муравей прополз всего по 5 ребрам куба. Значит, он прополз 60 см (5 ∙ 12).

Ответ: (D) 60 см.

Задача 5. 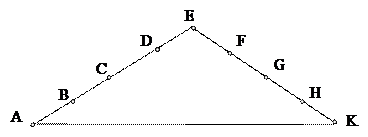(К-1999) Под горку Петя идет быстрее, чем в горку. На склонах горы отмечены точки A, B, C, D, E, F, G, H, K. Расстояния между соседними отмеченными точками одинаковы. Какой путь Петя пройдет быстрее?

(А) C →E→ G→ F (B) А →E→ F (C) D →E→ К→ Н (D) C →E→ Н (Е) D →E→ Н→ F

Решение. Обозначим время, затраченное на преодоление одного участка пути в горку b, а с горки c . Очевидно, что b > c.

Тогда на путь (А) C→E→ G→ F потратим 3b + 2c; на путь (B) А →E→ F потратим 4b + 2c;

на путь (C) D →E→ К→ Н потратим 2b + 4c; на путь (D) C →E→ Н потратим 2b + 3c;

на путь (Е) D→E→ Н→ F потратим 3b + 3c.

Остается попарно сравнить выражения и отбросить большие.

3b + 3c > 3b + 2c, отбросили (Е); 4b + 2c > 3b + 2c , отбросили (В);

2b + 4c > 2b + 3c, отбросили (С).

Осталось сравнить пути (А) и (D). 3b + 2c =(2b + 2c) + b; 2b + 3c = (2b + 2c) + c.

b > c, значит, путь (D) будет пройден за наименьшее время.

Ответ: (D) C →E→ Н.

Рассмотрим возможные виды движения двух тел.

1. Движение навстречу друг другу.

q

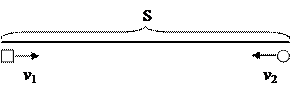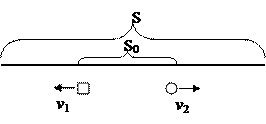
Если два тела движутся навстречу друг другу, то скорость «их сближения» равна сумме скоростей данных тел.

q Если первоначальное расстояние между двумя телами, движущимися навстречу друг другу со скоростями v₁ и v₂, равно S, то время, через которое они встретятся, равно:

t = S : (v₁ + v₂).

2. Движение в противоположные стороны.

q Если два тела движутся в противоположные стороны, то скорость «их удаления друг от друга» равна сумме скоростей данных тел.

q Расстояние между двумя телами, движущимися в противоположные стороны со скоростями v₁ и v₂, через время t равно

S = S₀ + (v₁ + v₂)× t,

где S₀ – первоначальное расстояние между ними. S₀ = 0, если движение тел начинается из одной точки.

3. Движение в одном направлении.

Если два тела, находящиеся перед началом движения на расстоянии S, движутся в одном направлении со скоростями v₁ и v₂, где v₂ > v₁, то возможны два случая.

1. Тело с большей скоростью догоняет тело с меньшей скоростью. В этом случае «скорость сближения» равна разности скоростей (v₂–v₁)_, а время, через которое второе тело догонит первое, равно:

t =S:(v₂ – v₁).

2. Тело с большей скоростью «убегает» от тела с меньшей скоростью. В этом случае «скорость удаления» также равна разности скоростей (v₂–v₁)_, а расстояние, которое будет между телами через время t, равно:

S₁ = S + (v₂ – v₁)× t

Разминка на «понимание» движения.

Два пешехода вышли из двух поселков, расположенных на одном шоссе.

Обозначим возможные виды движения двух пешеходов:

А – идут навстречу друг другу;

Б – идут в одном направлении;

В – удаляются друг от друга в противоположных направлениях.

Укажите, к какому виду движения относятся следующие утверждения (среди выражений могут встретиться неверные):

1. Сумма скоростей пешеходов определяет быстроту изменения расстояния между ними. (А; В)
2. Расстояние между пешеходами сокращается. (А; Б, если вторым идет тот, у кого большая скорость)
3. Произведение скоростей пешеходов определяет быстроту их сближения. (-)
4. В момент встречи расстояние между пешеходами равно нулю. (А; Б, если вторым идет тот, у кого большая скорость)
5. Разность скоростей пешеходов определяет быстроту изменения расстояния между ними. (Б)
6. После встречи расстояние между пешеходами будет увеличиваться. (А; Б, если вторым идет тот, у кого большая скорость)
7. После встречи расстояние между пешеходами будет уменьшаться. (-)
8. Расстояние между пешеходами увеличивается. (А, после встречи; Б, после встречи, если вторым идет тот, у кого большая скорость; Б, если вторым идет пешеход с меньшей скоростью)
9. Место встречи пешеходов зависит от их скоростей. (А, Б).
10. Время, прошедшее до встречи, зависит от расстояния между поселками. (А, Б).
11. Время, прошедшее до встречи, зависит от суммы скоростей пешеходов. (А).
12. Время, прошедшее до встречи, зависит от разности скоростей пешеходов. (Б).
13. Если скорости пешеходов одинаковые, то они встретятся ровно посередине между поселками. (А)
14. Если скорости пешеходов одинаковые, то они не встретятся. (Б, В)
15. Пешеходы обязательно встретятся, если будут идти достаточно долго.

Учителю. А – в любом случае. Б – конечно, подразумевается вариант, если вторым идет тот, у кого большая скорость. Но, можно поиграть, понимая слова «достаточно долго» как обход вокруг земного шара. Тогда Б – в любом случае, а так же В.

Следующая задача – на круговое движение.

Задача 6. На кольцевой дороге тренируются два велосипедиста. На дороге есть два контрольных пункта, расстояние между которыми – 400 м (по меньшей дуге) и 800 м (по большей дуге).

Из этих пунктов одновременно выехали на велосипедах Миша и Коля: Миша из первого - со скоростью 6 м в секунду, Коля из второго – со скоростью 4 м в секунду. Через какое время они окажутся рядом первый раз? (Рассмотреть все возможные случаи)

Решение:

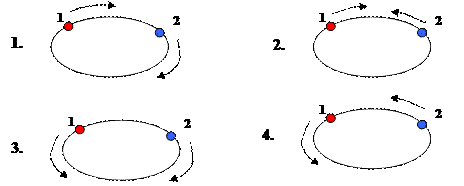
Возможны 4 варианта движения велосипедистов.

Сначала обсудите с учащимися следующие вопросы:

• Где изображено движение в противоположных направлениях («навстречу»)? (2 и 3)
• Каковы «скорости сближения» велосипедистов в этих случаях, и какая больше?

(Скорости сближения равны в обоих случаях, 6+4 =10 (м) за каждую секунду)

• Где изображено движение в одном направлении («вдогонку»)? (1 и 4)
• С какой скоростью Миша догоняет Колю в обоих случаях? (В обоих случаях скорость сближения мальчиков 6-4=2 (м) за секунду)
• В каком из этих случаев Миша быстрее догонит Колю? Почему?

(В первом случае, так как в этом случае первоначальное расстояние между мальчиками– 400 м, а во втором – 800 м)

Ответ:

1. В первом случае первая встреча произойдет через 200 секунд (400:2).

2. Во втором случае первая встреча произойдет через 40 секунд (400:10).

3. В третьем случае первая встреча произойдет через 80 секунд (800:10).

4. В четвертом случае первая встреча произойдет через 400 секунд (800:2).

Учителю. Можно обсудить с учащимися, через какое время будут происходить следующие встречи в каждом случае.

Задачи на движение можно решать разными способами: арифметическим, составляя уравнение и т.д. Но в любом случае необходимо четко представлять происходящий в задаче процесс. Затем выяснить, что неизвестно, и что играет определяющую роль для решения данной задачи. Наметить рациональный путь решения, при необходимости ввести условные величины, облегчающие счет.

Для нахождения алгоритма решения задачи часто достаточно составить таблицу v, t, S.

Полезно составить схему. Ее следует делать такой, чтобы была видна динамика движения со всеми характерными моментами – встречами, остановками и поворотами. Хороший чертеж позволяет понять содержание задачи, не заглядывая в ее текст.

Рассмотрим несколько задач:

Задача 7. Из аэропорта вылетели одновременно 2 самолета: один – на запад, другой – на восток. Через два часа расстояние между ними было 2800 км. Найдите скорость самолетов, если скорость одного составляла 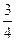скорости другого.

Решение.

1 способ.

Пусть х км/ч – скорость первого самолета, тогда 0,75х км/ч – скорость второго. Их общая скорость (скорость удаления друг от друга) – (х + 0,75х) км/ч, а общий путь за 2 часа – 2(х + 0,75х) км. Составляем уравнение: 2(х + 0,75х) = 2800. Решив уравнение, находим х = 800. Скорость первого самолета – 800 км/ч, скорость второго – 600 км/ч.

2 способ.

1) 2800 : 2 = 1400 (км/ч) – скорость удаления друг от друга двух самолетов.

2) 1 + 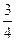= 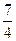– скорость удаления друг от друга двух самолетов в частях (если 1 – скорость первого самолета в частях, то 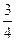- скорость второго самолета в частях).

3) 1400 : 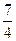= 800 (км/ч) – скорость первого самолета.

4) 800 × 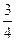= 600 (км/ч) – скорость второго самолета.

Ответ: 800 км/ч, 600 км/ч.

Задача 8. (К - 1997) Я прыгаю с трамплина в воду: сначала трамплин подбрасывает меня вверх на 1 м, затем я лечу вниз на 6 м и, выныривая, поднимаюсь на 2 м до поверхности воды. На какой высоте над водой находится трамплин?

(А) 1 (В) 2 (С) 3 (D) 4

(Е) трамплин находится под водой.

Решение. Нарисуем схему, точка отсчета - трамплин.

Ответ: (С) 3.

Задача 9. (Из «Всеобщей арифметики» И. Ньютона.) Два почтальона А и В находятся друг от друга на расстоянии 59 миль. Утром они отправляются навстречу друг другу. Почтальон А проходит в 2 часа 7 миль, В – в 3 часа 8 миль. Но почтальон В выходит часом позднее, чем А. Сколько миль пройдет почтальон А до встречи с почтальоном В?

Решение. За 1 час, пока почтальон В еще не вышел, почтальон А пройдет 3,5 мили, и расстояние между ними станет равным 55,5 мили. Скорость сближения почтальонов В и А равна ( 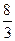+3,5) или 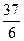мили в час, а пройти до встречи им вместе надо 55,5 или 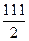мили. На это им понадобится

9 часов.

Ответ: 9 часов.

Задача 10. (К-2000)Опытный дрессировщик может вымыть слона за 40 минут, а его сыну для этого требуется 2 часа. За сколько времени они вымоют трех слонов, работая вдвоем?

(A) за 40 мин (B) за 45 мин (C) за 1 час (D) за 1,5 часа (E) за 1 час 40 мин

Решение.

Учителю. Можно заполнить табличку v, t, S и представить тело слона как путь, который пройдут щетки в процессе мытья.

Скорость мытья слона у дрессировщика 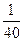сл./мин.

	v (сл/мин)	t (мин)	S (сл)
Дрессировщик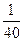
Сын дрессировщика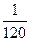
Вместе	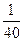+ 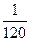=	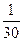?	3

Скорость мытья слона у его сына 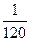сл/мин. Их общая скорость 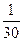сл/мин, то есть, одного слона они вдвоем моют за 30 мин.

Их ожидает путь в 3 слона, значит, им необходимо время 90 минут (3 : 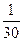или 3∙30).

Ответ: (D) за 1,5 часа.

Задача 11. Два пешехода одновременно вышли из пунктов А и В навстречу друг другу и встретились через полчаса, после чего продолжили путь каждый в своем направлении. Найдите расстояние между пунктами А и В, если известно, что скорость пешехода вышедшего из пункта А на 1 км/ч больше скорости второго и дошел он до пункта В через 24 минуты после встречи.

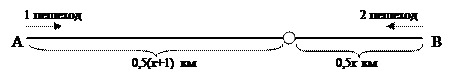Решение. Пусть скорость второго пешехода х км/ч, тогда (х + 1) км/ч – скорость первого.

До встречи первый пешеход прошел 0,5(х +1) км, а второй – 0,5х км. Первому пешеходу после встречи до пункта В осталось пройти 0,5х км – тот путь, который прошел второй пешеход до встречи. Вторую часть пути первый пешеход прошел за (0,5х):(х+1) ч, а так как это время 24 минуты или 2/5 часа, составляем уравнение: (0,5х):(х+1) = 2/5. Решаем уравнение, получаем х =4. То есть, 4 км/ч – скорость второго пешехода, 5 км/ч – скорость первого, 9 км/ч – скорость сближения, значит, расстояние между А и В – 4,5 км.

Ответ: 4,5 км.

Задача 12. (К-1996) Поезд из Москвы во Владивосток едет 7 суток и 1 час. Каждый день в 12 часов по московскому времени из этих городов выезжает по одному поезду. Сколько поездов, вышедших из Владивостока, встретит поезд, вышедший из Москвы?

(А) 7 (B) 6 (C) 8 (D) 14 (Е) 15

Решение. В момент выхода поезда А из Москвы на пути от Москвы до Владивостока уже будет находиться 7 поездов, вышедших из Владивостока в Москву за 7 дней до выхода поезда А (они отмечены на схеме). Поезд А обязательно встретит их все за время пути, но он также встретит и те 7 поездов, которые еще не вышли, но выйдут за семь дней пути поезда А. Последний пятнадцатый поезд встретится поезду А перед Владивостоком в последний час пути.

Ответ: (Е) 15.

Задача 13. В 11 часов утра из села вышел грузовик, а через час вслед за ним в том же направлении вышел автобус. Грузовик прибыл в город в 5 часов вечера, а автобус – раньше на час. Скорость автобуса на 25 км/час больше скорости грузовика. Какое расстояние между селом и городом?

Решение.

1 способ.

	v(км/ч)	t(ч)	S(км)
Грузовик	х		6х
Автобус	х + 25		4(х + 25)

Пусть х км/ч – скорость грузовика, тогда (х + 25) км/ч – скорость автобуса. Грузовик был в пути 6 часов, значит прошел расстояние 6х км, а автобус был в пути 4 часа, следовательно, прошел 4(х + 25) км. Так как они прошли одинаковые пути, составляем уравнение: 6х = 4(х +25). Решив уравнение, получаем х =50, значит расстояние между городами 6∙30=300 (км).

2 способ.

Грузовик был в пути 6 часов, а автобус - 4 часа.

Значит, скорость автобуса в полтора раза больше, чем скорость грузовика. А так как она на 25 км/ч больше, то скорость грузовика – 50 км/ч, а скорость автобуса – 75 км/ч.

Отсюда, расстояние между городами равно 300 км .

Ответ: 300 км.

Задача 14. Найдите длину поезда, зная, что он проходит мимо светофора за 8 с, а мимо платформы длиной в 400 м – за 28 с (скорость поезда постоянна).

Решение. Пусть длина поезда равняется х м, тогда его скорость 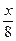м/с. За 28 секунд поезд пройдет 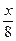∙ 28, а так как путь за 28 с равен длине платформы плюс длина поезда, то составляем уравнение: 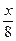∙ 28= х + 400. Решая уравнение, находим, что х =160. Значит, длина поезда равна 160 м.

Учителю. Обратите внимание, что путь за 8 секунд (мимо светофора) равен длине поезда, а путь за 28 секунд (мимо платформы) равен длине платформы плюс длина поезда.

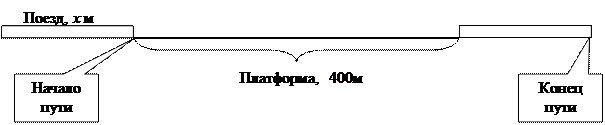
Ответ: 160 м.

Учителю. Следующую задачу из «Кенгуру-2002» можно рассмотреть только с наиболее сильными учениками, эту задачу решили всего 6% восьмиклассников.

Задача 15*.(К – 2002) Муха вылетает из Бухареста в Париж (2500 км) со скоростью 1 м/сек. Она удваивает скорость после каждого метра пути. Оцените время полета мухи.

(A)около 10 лет (B) около 2 лет (C) около 3 месяцев

(D) около суток (E) менее 2 секунд

Решение. Первый метр муха пролетит за 1 секунду, второй метр – за 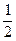секунды, третий – за 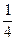секунды, четвертый – за 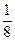секунды, и т.д. Итак, на каждый следующий метр муха затрачивает половину времени, оставшегося до истечения двух секунд. Значит, за 2 секунды она может улететь сколь угодно далеко, а не только в Париж.

Ответ: (Е) Менее 2 секунд.

Особые виды задач на движение – движение тел по воде. При решении таких задач необходимо помнить следующее:

• Скорость тела, движущегося по течению реки, равна сумме собственной скорости тела (скорость в стоячей воде) и скорости течения реки.
• Скорость тела, движущегося против течения реки, равна разности собственной скорости тела и скорости течения реки.
• Если в условии задачи речь идет о движении плотов, то этим хотят сказать, что тело (плот) движется со скоростью течения реки (собственная скорость плота равна нулю).
• Разность между скоростью тела по течению и против течения рекиравна удвоенной скорости течения реки.

Если x км/ч – собственная скорость тела, v км/ч – скорость течения реки, то

(x+v) км/ч – скорость тела по течению, (x-v) км/ч – скорость против течения.

Тогда разность между скоростью тела по течению и против течения:

(x + v) – (x - v) = x + v – x + v = 2v.

Задача 16. Крокодил проплыл 12 км вниз по течению Амазонки. Потом он сделал двухчасовую остановку на обед, развернулся и, проплыв меньше на 1 час, вылез на берег и улегся спать. Сколько км всего проплыл крокодил, если его собственная скорость на 2 км/ч больше скорости течения реки и равна 6 км/ч?

Решение.

1) 6 +2 = 8 (км/ч) – скорость крокодила по течению реки.

2) 12 : 8 = 1,5 (ч) – плыл крокодил по течению.

3) 1,5 – 1 = 0,5 (ч) – плыл крокодил против течения.

4) 6 – 2 = 4 (км/ч) – скорость крокодила против течения реки.

5) 4 × 0,5 = 2 (км) – проплыл крокодил против течения.

6) 12 + 2 = 14 (км) – весь путь крокодила.

Ответ: 14 км.

Задача 17. Расстояние между городами А и В пароход проплывает по течению реки за 3 часа, а против течения реки за 4,5 часа. За какое время проплывет то же расстояние бочонок, брошенный в воду?

Решение.

Расстояние между городами принимаем за 1.

1) 1 : 3 = 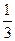– скорость парохода по течению реки в частях от расстояния (такую часть пути он проплывает за 1 час).

2) 1 : 4,5 = 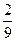– скорость парохода против течения реки в частях.

3) 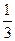– 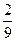= 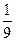- разница в скорости теплохода по течению реки и против течения, т.е. удвоенная скорость реки.

4) 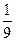: 2 = 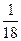- скорость течения реки.

5) 1 : 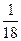= 18 (ч) - время движения бочонка.

Ответ: Бочонок проплывет расстояние между городами А и В за 18 часов.

Учителю. Можно составить табличку v, t, S. Но в ней будет два неизвестных – собственная скорость парохода и скорость течения. Составленное уравнение дает только пропорцию 5 :1, и тогда движение по течению произошло со скоростью в 6 раз большей, чем скорость течения, и значит, время бочонку понадобится в 6 раз больше чем пароходу.