Көлденең иілу кезіндегі кернеулер

Көлденең иілу кезінде Q≠0, M=vary, сонда көлденең қималарында тек қана σ тік кернеулері емес, τ жанама кернеулері де пайда болады. τ болған кезде γ бұрыштық деформациясы да болады, сонда τ мен γ қима бойымен бірқалыпты таралмаған соң, сырықтың көлденең қималары жазық болып қала бермейді. Бірақ бұл σ мәндеріне айтарлықтай әсерін тигізбейді, сонда (11.5) пен (11.6) жеткілікті нақтылықпен орындалады деп есептеуге болады.

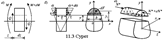Көлденең қимада b ені бойынша τ бірқалыпты таралады деп алып, оларды бейтарап сызықтан y қашықтығында орналасқан бойлық қимадағы жұптық кернеулері арқылы табуға ыңғайлы болады (11.3 сурет).

Ұзындығы dz элементінен бойлық қимасымен кесіп алған бөлігі үшін тепе-теңдік теңдеулерін жазып, жанама кернеулер үшін Журавскийдің формуласын аламыз

(11.9)

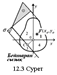мұндағы 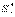- бойлық қимасынан жоғары алынған қөлденең қимасы бөлігінің x өсіне қатысты статикалық моменті.

Көптеген жағдайда τ сырықтардың беріктігіне әсерін тигізбейді (жұқа қабырғалы және қысқа сырықтардан басқасы үшін). Сонда көлденең қимасы тұрақты, созылу мен сығылуға бірдей қарсылысатын материалдан жасалған сырық үшін көлденең иілу кезіндегі беріктік шарты келесі түрде жазылады

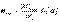(11.10)

Сырықтың майысқан өсінің дифференциалдық теңдеуі және оны

Интегралдау

Жазық иілу кезінде арқалықтың майысқан өсі көлденең жүктемелер жатқан жазығындағы қисық сызық болып келеді. Өстің нүктелері көлденең бағытта орын ауыстырады және көлденең қималар бейтарап сызыққа қатысты бұрылады. Сызықтық орын ауыстыруларды (ойысуларды) v деп және бұрыштық орын ауыстыруларды θ деп белгілейміз. θ бұрышы майысқан өске жүргізілген жанамамен сырықтың бастапкы өсі жасайтын бұрышқа тең (11.5 сурет). v мен θ шамалары z координаттыңфункциясы болып табылады; оларды қатаңдыққа есептеу жүргізу үшін білу қажет. zy координаттар жүйесінің басын арқалықтың сол жақтағы шетімен біріктіріп, мыныған көз жеткіземіз: v(z)=y(z), tgθ(z)=y′(z), мұндағы y(z) – арқалықтың майысқан өсінің теңдеуі. Сонымен v мен θ шамаларын табу есебі y(z) арқалықтың майысқан өсінің теңдеуін табу есебіне келтірілді.(11.5) тауелділігі орындалады деп есептейміз. y(z) сызығы үшін қисықтығын былай өрнектеуге болады 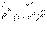. 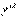<<1 болғандықтан, 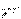. Осыны ескере отырып, сырықтың майысқан өсінің дифференциалдық теңдеуін мыны түрде аламыз

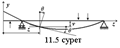
. (11.11)

Бұл теңдеуді аналитикалық түрде тек қарапайым жағдайларда ғана мүмкін. Интегралдаудан шағатын тұрақтылар шекаралық шарттардан табылады.

, .

Иғаш иілу

Қиғаш иілу кезінде июші моменттің жазықтығы көлденең қиманың бас инерция өстерінің біреуінен де өтпейді (12.5 сурет). Қи-ғаш иілуді біржолы екі, x және y бас инерция өстеріне қатысты иілу ретінде қарастырған ыңғайлы. Ол үшін жалпы М июші моментінің векторын M_x = Msin және M_y = Mcos құраушы моменттеріне жіктеу керек. Координаттары x пен y нүктедегі тік кернеу келесі формуламен табылады

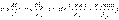.(12.11)

Кернеулер нүктелердің БС дейін қашықтықтарына пропорционал болады, БС теңдеуі осылай жазылады

.(12.12)

J_x≠J_y болғандықтан, қиғаш иілу кезінде БС июші моменттің жазықтығына перпендикуляр емес, яғни сырық июші моменттің жазықтығында иілмейді, ол басқа, иілуге қатаңдығы аз жазықтықта иіледі.