Основные теоремы теории вероятностей и их следствия.

1) Докажите, что если события А и В независимы, то и события А и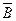

также независимы.

2) Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8 производят по одному выстрелу. Определите вероятность:

а) хотя бы одного попадания в мишень;

б) одного попадания в мишень.

3) Рабочий обслуживает 3 станка, каждый из которых работает независимо от двух других. Вероятности того, что за смену станки не потребуют вмешательства рабочего, равны соответственно

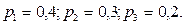
Найдите вероятность того, что за смену по крайней мере один станок потребует вмешательства рабочего.

4) Найти вероятность того, что наудачу взятая кость из игры домино содержит не менее 4 и не более 6 очков

5) Бросается монета до 1-го появления « герба». Найти вероятность того, что потребуется четное число бросков.

6) Три станка производят соответственно 50%, 30% и 20% всех изделий. В их продукции брак составляет соответственно 1%, 2% и 1,5%. Какова вероятность того, что выбранное наугад изделие окажется бракованным?

7) Радиолампа поступила с одного из 3-х заводов соответственно с вероятностями 0,25; 0,50 и 0,25. Вероятность выйти из строя в течение года для ламп, изготовленных 1-м заводом, равна 0,1, 2-м

заводом – 0,2 и 3-м – 0,4. Определить вероятность того, что лампа проработает год.

Тема: Прямые и плоскости в пространстве

1. Докажите, что если точки А, В, С и D не лежат на одной плоскости, то прямые АВ и CD не пересекаются.

2. Если четыре точки не лежат в одной плоскости, могут ли какие то три из них лежать на одной прямой?

3. Докажите, что если прямые АВ и CD не лежат в одной плоскости, то прямые АС и BD тоже не лежат в одной плоскости.

4. В пространстве даны четыре точки, никакие три из них не лежат на одной прямой. Через каждую пару точек проведена прямая. Сколько таких прямых можно провести?

5. В пространстве даны 4 точки, не лежащие в одной плоскости. Через каждые три из них проведена плоскость. Сколько таких плоскостей можно провести?

6. Докажите, если две прямые АВ и CD скрещиваются, то прямые АС и BD тоже скрещиваются.

7. Прямая l пересекает прямую а и не пересекает прямую b, которая параллельна прямой а. Докажите, что прямые b и l скрещиваются.

8. Прямая l параллельна стороне BC параллелограмма ABCD. Найти угол между прямыми l и CD, если один из углов параллелограмма равен: а) 55°; б) 129°.

9. Будут ли параллельны две прямые, которые параллельны одной плоскости? Могут ли такие прямые пересекаться? Скрещиваться?

10. Точки А и В лежат в плоскости р, а точка М не лежит в этой плоскости. Доказать, что прямая, проходящая через середины отрезков АМ и ВМ, параллельна плоскости р.

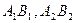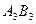11. Три отрезка и , не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскост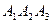и и 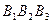параллельны.

12. Через точки А и В одной из двух параллельных плоскостей проведены параллельные прямые, пересекающие вторую плоскость в точках 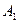и 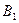. Чему равен отрезок 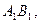если отрезок АВ = а ?

13. Известно, что прямая l параллельна прямой т , которая параллельна плоскости р. Будет ли прямая l параллельна плоскости р ?

14. Докажите, что отрезки параллельных прямых, заключенных между параллельными плоскостями, равны.

15. Дано: l ll т

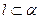
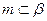
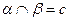
Доказать: с ll l ll m.

16. Верно ли утверждение, что: две прямые, параллельные некоторой плоскости, параллельны между собой? Обосновать.

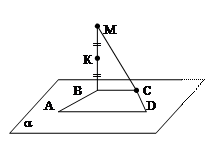
17. На рисунке в плоскости a изображена трапеция АВСD, основание ВС которой равно 12см. Точка М не лежит в плоскости a , а точка К – середина отрезка ВМ . Доказать, что плоскость АDК пересекает отрезок МС в некоторой точке Н . Найти отрезок КН.

18. В 4 - угольной пирамиде АВСDЕ основание АВСD – трапеция, ВС ll AD. Построить прямую х , по которой пересекаются плоскости граней ВСЕ и ADE. Как расположены прямые: а) ВС и х; б) AD и х; в) АВ и х; г) DE и х ?

19. Плоскости a и b параллельны, прямая т лежит в плоскости a. Доказать, что прямая т параллельна плоскости b.

20. Точка М не лежит в плоскости прямоугольника ABCD . Доказать, что прямая CD параллельна плоскости АВМ.

Тема: Построение сечений.

1. В кубе 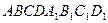постройте сечение плоскостью, проходящей через: а) середины ребер, выходящих из одной вершины; б) три точки, лежащие на ребрах ; .

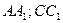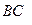2. Дан тетраэдр SАВС и точки M и N , где 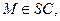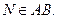Построить пересечение плоскостей АВМ и SCN. Обосновать.

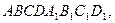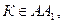
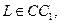
3. Дан куб причем 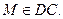Постройте сечение куба плоскостью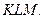

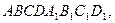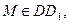
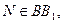
4. Построить линию пересечения плоскостей АВС и MNP параллелепипеда где 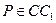( 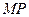ll DС, PN ll BC ).