Исследование функций и построение графика функции

Первое представление о графике функции получаем из вида 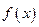, а именно область определения, частные свойства (периодичность, четность, нечетность), нули функции и промежутки, где функция сохраняет знак. Знание пределов и производных позволяет определить асимптоты, экстремумы, выпуклость.

Монотонность, экстремумы. Характер (возрастание или убывание) функции на промежутке связан с первой производной. Если для всех точек промежутка 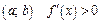, то функция возрастает на этом промежутке, если 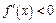, то функция убывает. Функции, возрастающие или убывающие на промежутке, называются монотонными.

Пусть задана функция 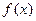, непрерывная в точке 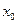и ее окрестности. Если для всех значений 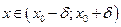выполнено неравенство 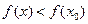, то функция имеет в точке 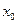строгий максимум, а точка 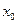называется точкой максимума. Значение максимума вычисляется как значение функции 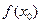. Аналогично определяется точка минимума. Точки максимума и минимума называются точками экстремума.

Необходимым условием существования экстремума дифференцируемой функции является равенство нулю ее производной. Из уравнения 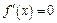находим значения 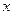, в которых возможен экстремум (точки, подозрительные на экстремум). Достаточное условие существования экстремума – изменение знака производной при переходе через точку 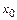, в которой .

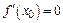Выпуклость, вогнутость. Для исследования выпуклости (вогнутости) графика функции используется вторая производная.

График функции выпукла вверх, если 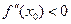, вогнута вверх, если .

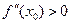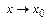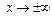Асимптоты. Асимптотой называется прямая линия такая, что, если двигаться по графику функции в указанном направлении или , расстояние до соответствующей прямой (асимптоты) стремится к нулю. Различают асимптоты: вертикальные и невертикальные.

Вертикальной асимптотой называется прямая линия 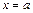такая, что выполняется хотя бы одно из равенств

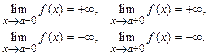(4)

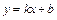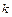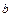Невертикальная асимптота имеет уравнение , где параметры и определяются при помощи пределов:

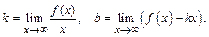(5)

При этом предела в формуле (5) должны быть конечны. В случае 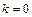имеем дело с горизонтальной асимптотой.

Пример 5.Исследовать функцию 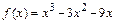на наличие экстремумов и определить промежутки возрастания, убывания.

Решение. Данная функция определена и дифференцируема на всей числовой оси.

.

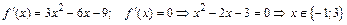Определяя знаки выражения 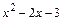на интервалах 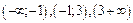, делаем вывод о том, что функция возрастает на промежутках 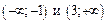, убывает на промежутке 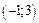, имеет максимум в точке 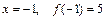и минимум в точке .

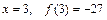Пример 6. Исследовать функцию 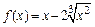на наличие экстремумов и определить промежутки возрастания, убывания.

Решение. Область определения функции .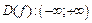

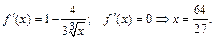
В точке 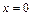производная не существует. Отметим на числовой оси промежутки знакопостоянства для производной.

Вывод: функция возрастает на промежутках 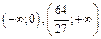, убывает на промежутке 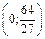, имеет максимум в точке 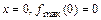и минимум в точке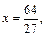

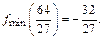
Анализ функции будем проводить поэтапно:

1. по самой функции,
2. по первой производной,
3. по второй производной.

	область определения, частные свойства: четность, нечетность, периодичность, точка пересечения с осью , поведение на границе области определения и нахождение асимптот, определение нулей функции и промежутков знакопостоянства.
	вычисление производной и определения области ее существования, определение стационарных точек и промежутков монотонности функции,
	вычисление второй производной и определения области ее существования, определение нулей второй производной и промежутков выпуклости, вогнутости.

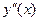На основании всех проделанных вычислений составим таблицу. В первой строке запишем все значения 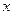, полученные в пунктах 1,5,7,9 и интервалы, на которые эти точки делят числовую ось, во второй строке - информацию для 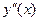, в третьей строке – информация для 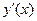. Четвертая строка – заключительная. В нее запишем информацию для функции 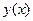. Для наглядности используем следующие значки:

Функция возрастающая и выпуклая вверх ─ ,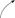

Функция убывающая и выпуклая вверх ─ .

Функция возрастающая и вогнутая ─ .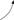

Функция убывающая и вогнутая ─ .

Рассмотрим на примерах построение графиков нескольких функций.

Пример 7. Построить график функции .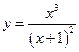

Решение.

Пройдем по пунктам предложенный выше алгоритм. При этом в пунктах 5,7,9 определим только нули функции или ее производных, а определение промежутков знакопостоянства оставим до таблицы.

1. Функция определена для всех 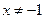, то есть .

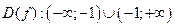2. Функция не обладает свойствами периодичности, четности, нечетности.

3. .

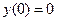4. 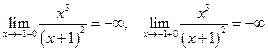. Следовательно, прямая 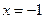- вертикальная асимптота для графика функции.

Для определения существования наклонных асимптот вычислим значения 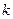и .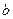

.

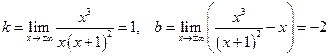Следовательно, прямая 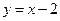- наклонная асимптота, причем график функции стремится к этой линии и при 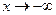, и при .

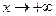5. .

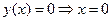6-7. .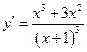

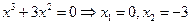8-9. .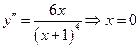

Составим таблицу, разбив числовую ось точками , , .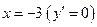

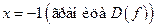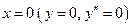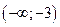		-3		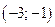-1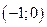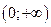
					+
	+			+		+
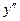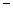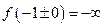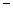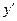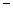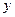		Max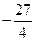

Фактически в последней строке виден график функции. Осталось его привязать к системе координат и изобразить асимптоты.

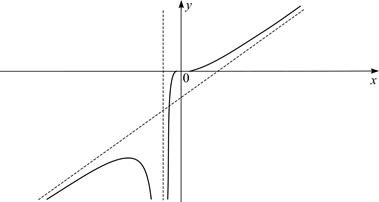
Рис. 2

Пример 8. Построить график функции .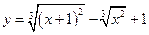

Решение.

1. Функция определена для всех, то есть .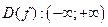

2. Функция не обладает свойствами периодичности, четности, нечетности.

3. .

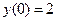4. Вертикальных асимптот нет.

Для определения существования наклонных асимптот вычислим значения 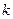и .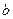

.

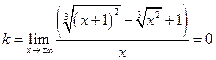
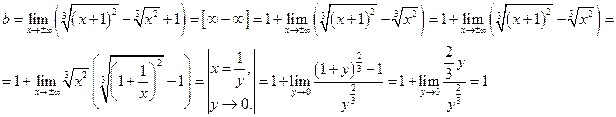Следовательно, прямая 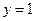- наклонная (горизонтальная) асимптота, причем график функции стремится к этой линии и при 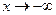, и при .

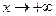5. .

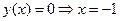6-7. 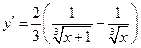. Ни в одной из точек первая производная не обращается в нуль. Однако при значениях 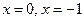производная не существует, и эти точки могут оказаться экстремумами.

8-9. 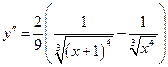. Естественно вторая производная не существует при значениях 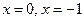и равна нулю, если .

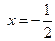Составим таблицу

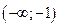		-1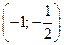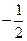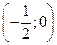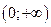
					+		+
			+		+
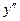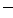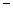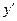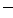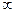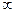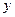		Min				Max

График имеет вид, приведенный на рис. 3.

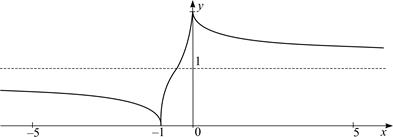
Рис. 3

Пример 9. Построить график функции .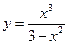

Решение.

1. Функция определена для всех 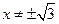, то есть .

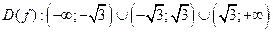2. Функция не обладает свойствами периодичности, но является нечетной функцией. Далее можем рассматривать функцию только для положительных значений аргумента.

3. .

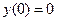4. 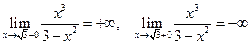. Следовательно, прямая 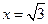- вертикальная асимптота для графика функции.

Для определения существования наклонных асимптот вычислим значения 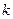и .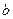

.

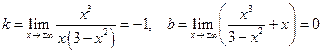Следовательно, прямая 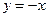- наклонная асимптота, причем график функции стремится к этой линии и при 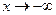, и при .

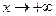5. .

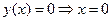6-7. 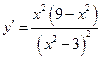. Неотрицательные корни производной: .

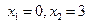8-9. .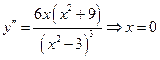

Составим таблицу, разбив неотрицательную часть числовой оси точками , .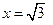

		+
		+	+
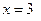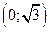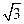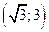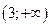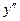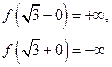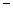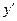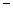				Max -9

Построим функцию для положительных значений аргумента и, воспользовавшись свойством нечетности, продолжим график влево. Окончательный вариант графика представлен на рис. 45.

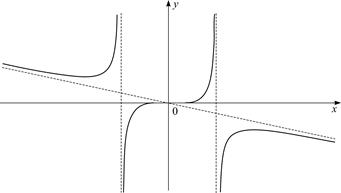
Рис. 4
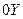