Силовой расчет структурных групп

4.6.1. Силовой расчет группы 1-го вида

Дано: , , , – внешние силы и моменты пар сил (в том числе силы инерции), приложенные к звеньям 2 и 3.

Определить: , , – реакции в кинематических парах (рис. 24).

а) б)

Рис. 24. Силовой анализ структурной группы 1-го вида:

а) расчетная схема; б) план сил

Решение: Неизвестные реакции покажем пунктиром и разложим на две составляющие так, чтобы момент одной из них относительно точки В был равен нулю:

– нормальная составляющая реакции; направлена по звену АВ;

– касательная составляющая; направлена перпендикулярно звену АВ.

Аналогично разложим реакцию (рис. 24, а), направив по звену ВС; – перпендикулярно звену ВС.

Направления векторов принимаем произвольно.

Уравнение равновесия звена 2относительно точки B:

, (4.8)

где – момент силы относительно точки В;

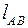– длина звена АВ (плечо силы ).

Сумма моментов принимается алгебраической, т. е. при решении уравнений учитывается направление моментов сил.

Из уравнения (4.7) имеем

. (4.9)

При численных расчетах результат может оказаться и со знаком «плюс»,
и со знаком «минус». Если получится знак «плюс», значит, направление вектора силы реакции принято правильное; если знак «минус», то направление вектора следует изменить на противоположное.

Уравнение равновесия звена 3относительно точки B

, (4.10)

отсюда

. (4.11)

Уравнение равновесия для всей группы

. (4.12)

В векторном уравнении (4.11) неизвестны величины сил и , но заданы их направления.

Для того чтобы векторная сумма всех сил равнялась нулю, силовой многоугольник должен быть замкнут. Следовательно, решением уравнения (4.11) будет точка пересечения направлений сил и .

Построим уравнение (4.11) путем обычного сложения векторов (рис. 24, б). Откладываем из точки а последовательно все известные силы, начиная с
в масштабе сил 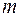_F . В точке b, где находится конец вектора , начинается вектор . Проводим через точку b перпендикуляр (направление нормальной составляющей реакции). В точке а должен находиться конец вектора , при этом силовой многоугольник замкнется. Проводим через точку а перпендикуляр к вектору . Точка пересечения проведенных двух прямых (точка с) определяет величину реакций и .

Графическое изображение векторных уравнений равновесия звеньев или структурных групп называется планом сил.

Сравним направление полученных на плане сил реакций с произвольно заданными на расчетной схеме (рис. 24, а). Очевидно, что реакции и предположительно были заданы неверно, в действительности векторы направлены в противоположную сторону. В таких случаях направления реакций на расчетной схеме следует изменить.

По плану сил определяется равнодействующая реакций и , а также истинные направления этих векторов (на плане сил показаны пунктиром).

Определим реакцию в шарнире В. Для этого рассмотрим уравнение равновесия одного из звеньев, например, звена 2. Отброшенное звено 3 заменим его реакцией на звено 2, т. е. в данном случае выступает как внешняя сила.

Уравнение равновесия звена 2

. (4.13)

Первые два вектора уже построены (рис. 24, б), остается соединить конец вектора с началом вектора , чтобы силовой треугольник был замкнут. Зная масштаб построения плана сил 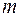_F , можно определить значение вектора .

4.6.2. Силовой расчет группы 2-го вида

Дано: , , , – внешние нагрузки, действующие на звенья 2 и 3.

Определить: , , , h – реакции в кинематических парах и точку приложения реакции в поступательной паре (рис. 25).

а) б) в)

Рис. 25. Силовой анализ структурной группы 2-го вида:

а) расчетная схема; б) план сил; в) распределение реакций в поступательной паре

Решение: Разложим реакцию во вращательной паре (в шарнире А) на две составляющие (рис. 25, а).

Уравнение равновесия звена 2

, (4.14)

отсюда

. (4.15)

Уравнение равновесия всей группы

. (4.16)

Векторы и известны только по направлению, остальные – и по направлению, и по величине.

Строим векторное уравнение в виде плана сил, начиная с известного вектора (рис. 25, б), откладывая из точки а последовательно все известные силы в масштабе . Чтобы замкнуть силовой многоугольник, проводим через точку а перпендикуляр к , а через точку b – направление вектора (перпендикулярно оси движения ползуна х-х). Точка пересечения этих двух линий определяет величину векторов и . Полную реакцию находим как равнодействующую и (на плане обозначена пунктиром).

Определим реакцию в шарнире В. Для этого рассмотрим уравнение равновесия одного из звеньев, например, звена 2. Отброшенное звено 3 заменим его реакцией на звено 2, т. е. в данном случае выступает как внешняя сила.

Уравнение равновесия звена 2

. (4.17)

Замыкая силовой треугольник на плане сил, находим неизвестный вектор . Зная масштаб построения плана сил 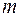_F, определяем значение вектора .

Из уравнения равновесия звена 3определим точку приложения реакции
в поступательной паре:

, (4.18)

отсюда

. (4.19)

Если плечо h получится со знаком «минус», то это значит, что точку приложения силы следует расположить по другую сторону от точки В. Тогда момент будет иметь противоположный знак.

Очень часто при решении задач плечо h получается таким, что сила оказывается далеко за пределами кинематической пары. Рассмотрим, как воспринимается в этом случае реакция элементами кинематической пары (рис. 43, в). Плечо силы относительно центра поступательной пары обозначим . Прикладывая в центре пары две равные и противоположно направленные силы , получим силу , приложенную в центре, и момент пары сил, равный , который будет действовать в крайних точках ползуна, т. е. на плече l.

Реакция от момента в крайних точках l:

, (4.20)

где l – длина ползуна.

Таким образом, действие силы на плече h будет в действительности передаваться как сила , приложенная в центре ползуна, и пара сил , приложенная на плече l.

Такое расположение реакций неблагоприятно сказывается на работе ползуна, так как вызывает значительные силы трения.

4.6.3. Силовой расчет группы 3-го вида

Дано: , , , – внешние силы и моменты пар сил, приложенные к звеньям 2 и 3(рис. 26).

Определить: , , – реакции в кинематических парах; h – плечо реакции в поступательной паре.

а) б)

Рис. 26. Силовой анализ структурной группы 3-го вида:

а) расчетная схема; б) план сил

Решение: Неизвестные реакции и раскладываем на две составляющие: параллельную х-х и перпендикулярную х-х (рис. 26, а).

Реакция направлена перпендикулярно х-х.

Уравнение равновесия звена 2 запишем в виде суммы проекций на ось х-х

, (4.21)

отсюда: .

Уравнение равновесия звена 3 (сумма проекций на ось х-х):

, (4.22)

отсюда: .

Уравнение равновесия всей группы:

. (4.23)

Строим это уравнение в масштабе плана сил (рис. 44, б).

Из точки а отложим векторы , , , , получим точку b, из которой проводим перпендикуляр к линии х-х (направление векторов и ). Поскольку векторы параллельны между собой, то для выполнения равенства (4.22) необходимо попасть в точку а, чтобы замкнуть силовой многоугольник. Таким образом, отрезок ab представляет собой в масштабе сумму векторов и .

Плечо силы относительно точки А обозначим через (его можно измерить на схеме и вычислить с учетом масштаба длин) и составим еще одно уравнение.

Уравнение равновесия для всей группы (сумма моментов относительно точки А):

,

отсюда

(4.24)

где , , – моменты сил относительно точки A.

После этого откладываем величину в масштабе 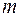_F от точки b по линии ab,оставшийся участок – это сила (отрезок са).

Равнодействующие и обозначены пунктиром.

Определим реакцию в поступательной паре из уравнения равновесия звена 2:

. (4.25)

Первые два вектора уже есть на плане. Отрезок dc изображает замыкающий вектор – реакцию .

Определим точку приложения реакции из уравнения равновесия звена 2:

, (4.26)

отсюда: .

Полученная величина определяет, на каком расстоянии от точки А приложена реакция .

4.6.4. Силовой расчет начального звена

Для того чтобы привести механизм в движение и выполнить полезную работу, необходимо выбрать мощность двигателя, которая обеспечила бы вращение начального звена с определенной скоростью. При постоянной скорости вращения движущая сила (момент сил) должна уравновешивать все силы, приложенные к начальному звену. Поэтому в задачу силового расчета начального звена, кроме определения реакций, входит еще и определение внешнего силового фактора.

Если передача энергии осуществляется через зубчатый редуктор, то внешний силовой фактор представляет собой силу , действующую по нормали к рабочей поверхности зуба (рис. 27, а).

а) б) в)

Рис. 27. Силовой анализ начального звена:

а) расчетная схема при передаче энергии через редуктор; б) план сил; в) при передаче энергии через муфту

В соответствии с геометрией стандартных зубчатых колес нормаль в точке касания зубьев образует угол = 20^о с перпендикуляром к межосевому расстоянию.

Кроме уравновешивающей силы , на начальное звено действуют реакции со стороны отброшенного звена 2( ), а также реакция стойки ( ).

Как было упомянуто выше, . Сила определена предыдущим расчетом структурной группы. Таким образом, имеется неизвестная по величине и по направлению сила и неизвестная по величине сила .

Сила определяется из уравнения

, (4.27)

где – момент силы относительно точки O;

– плечо силы (рис. 27, а).

Реакция стойки определяется из уравнения

(4.27)

Строим векторное уравнение в виде плана сил, замыкающая сторона треугольника изображает реакцию стойки (рис. 27, б).

В том случае, если передача энергии осуществляется через муфту, внешний силовой фактор представляет собой момент (рис. 27, в). Отброшенное звено 2 заменяем реакцией . Если на звено 1 не действуют никакие другие силы, то реакция стойки .

Уравновешивающий момент:

.

4.7. Определение уравновешивающей силы
методом Жуковского

При определении мощности двигателя, расчете маховика на ведущем валу и в других подобных задачах необходимо знать только уравновешивающую силу, приложенную к начальному звену. Реакции в кинематических парах при этом определять не требуется. В таких случаях применяется метод Жуковского. Теорема Жуковского основана на известном из теоретической механики принципе возможных перемещений.

Сумма элементарных работ внешних сил на их возможных перемещениях равна нулю.

На основании принципа возможных перемещений можно записать:

,

где , , …, – внешние силы и силы инерции, приложенные к звеньям механизма;

, , …, – проекции элементарных перемещений на направления соответствующих сил.

Для определения элементарной работы силы на ее элементарном перемещении рассмотрим звено АВ, в точке S которого приложена сила под углом 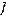к скорости точки S (рис. 28, а).

а) б)

Рис. 28. К выводу теоремы Жуковского:

а) расчетная схема; б) план скоростей

Строим план скоростей в масштабе 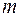_V, считая, что скорости точек и известны. Скорость точки S определяем по принципу подобия (рис. 28, б).

Силу повернем на 90^о в любую сторону и перенесем на план скоростей в точку S. Плечо этой силы относительно полюса обозначим через .

Работа силы на элементарном перемещении

, (4.28)

но , поэтому

. (4.29)

Момент силы , относительно полюса плана скоростей:

. (4.30)

Окончательно имеем:

. (4.31)

С учетом принципа возможных перемещений (4.28) суммируем элементарные работы и приравниваем их к нулю:

. (4.32)

Сокращая выражение (4.32) на , получим:

. (4.33)

Выражение (4.33) и представляет собой теорему Жуковского, которая формулируется следующим образом.

Сумма моментов всех внешних сил, приложенных в соответствующих точках плана скоростей и повернутых на 90° относительно полюса плана скоростей, равна нулю.

Поворачивать можно либо силы, либо план скоростей. Иначе говоря, повернутый план скоростей можно представить как жесткий рычаг, находящийся в равновесии под действием приложенных внешних сил. Поэтому данную теорему иногда еще называют теоремой о жестком рычаге Жуковского. Пользуясь ею, можно сразу находить уравновешивающую силу, минуя силовой расчет структурных групп.

Предположим, чтозаданы силы, действующие на звенья механизма
, , …, . Требуется найти уравновешивающую силу – . Плечи сил, перенесенных в соответствующие точки повернутого на 90° плана скоростей, относительно полюса ( , , …, , ) находятнепосредственным измерением.

Тогда, согласно теореме Жуковского, имеем

,

отсюда

. (4.34)

Если на звенья механизма действуют еще и моменты, то их раскладывают на пары сил, приложенные в точках, скорости которых известны.

СИЛЫ ТРЕНИЯ В МЕХАНИЗМАХ

Виды трения

Силы трения возникают в кинематических парах при относительном движении звеньев, они обусловлены реакциями связей и являются составляющими этих реакций. Поэтому силы трения можно считать внутренними по отношению ко всему механизму и внешними по отношению к отдельным звеньям.

В большинстве случаев силы трения относятся к силам сопротивления, но иногда движение передается благодаря силам трения, и в этом случае они относятся к движущим силам (например, в ременной передаче движение передастся за счет трения ремня о шкив).

В зависимости от характера относительного движения элементов кинематических пар различают следующие виды трения:

- трение скольжения, которое возникает в низших кинематических парах;

- трение качения (или качение со скольжением), которое возникает в высших кинематических парах.

В зависимости от состояния трущихся поверхностей различают несколько видов трения скольжения:

- сухое трение, при котором поверхности соприкасаются непосредственно (рис. 29, а);

- жидкостное трение, при котором поверхности разделяются слоем смазки (рис. 29, б).

а) б)

Рис. 29. Виды трения:

а) сухое; б) жидкостное

Кроме того, существуют промежуточные виды трения – полусухое и полужидкостное, в зависимости от того, какой вид трения преобладает.

По своей природе силы сухого и жидкостного трения различны, поэтому различны и методы их учета. При сухом трении сила трения представляет собой сумму элементарных составляющих реакций в точках контакта поверхностей ( ) и величина её определяется законом Кулона

, (5.1)

где – сила трения;

– коэффициент трения, зависящий от физико-механических свойств соприкасающихся поверхностей;

– нормальная составляющая реакции в кинематической паре.

Величина силы жидкостного трения рассчитывается по формуле:

, (5.2)

где – диссипативный коэффициент, зависящий от свойств смазки и толщины слоя смазки.