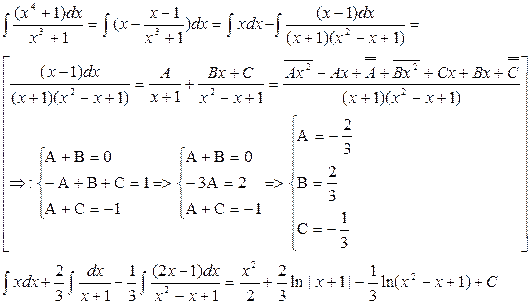Экстремум функции двух независимых переменных
Говорят, что функция z = f(x, y) имеет максимум в точке М0(х0, у0), если f(x0, y0) > f(x, y)и минимум, если f(x0, y0) < f(x, y) для всех точек, достаточно близких к М0 и отличных от нее. Максимум и минимум называют экстремумами функции. Экстремумы можно определить и иначе: Положим х = х0 + Dх и у = у0 + Dу, тогда f(х + Dх, у + Dу) – f(х0, у0) = Df. Если Df > 0 при всех достаточно малых приращениях независимых переменных, то функция f(x, y) достигает минимума в точкеМ0. Если Df < 0 при всех достаточно малых приращениях аргументов, то функция f(x, y) достигает максимума в точке М0.
Определения эти справедливы для функций любого числа переменных. Необходимое условие экстремума можно сформулировать так:
Если функция z = f(x, y) достигает экстремума при х = х0, у = у0, то каждая частная производная первого порядка от z или обращается в нуль при этих значениях аргументов, или не существует.
Действительно, если функция z = f(x, y) имеет в некоторой точке М0(х0,у0)экстремум, в этой точке имеют экстремум и функции одной переменной z = f(х0, у) и z = f(х, у0) и, соответственно, их производные 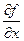 и
и 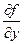 в этой точке или равны нулю или не существуют. Точки, в которых выполняются эти условия, называются критическими, и в этих точках может быть (а может и не быть) экстремум. Критические точки, в которых zx` = 0 и zу` = 0 называют стационарными. О наличии экстремума в стационарных точках можно во многих случаях судить на основании следующей теоремы:
в этой точке или равны нулю или не существуют. Точки, в которых выполняются эти условия, называются критическими, и в этих точках может быть (а может и не быть) экстремум. Критические точки, в которых zx` = 0 и zу` = 0 называют стационарными. О наличии экстремума в стационарных точках можно во многих случаях судить на основании следующей теоремы:
Если в некоторой области, содержащей точку М0(х0, у0), функция имеет непрерывные частные производные до третьего порядка включительно и точка М0 является стационарной, то в этой точке:
Функция имеет максимум, если D > 0, а A < 0 или (C < 0)
Функция имеет минимум, если D > 0, а A > 0 или (C > 0)
Функция не имеет экстремума, еслиD < 0
Если D = 0 – сомнительный случай, требуется дополнительное исследование.
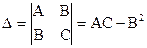 (4.12) , где:
(4.12) , где: 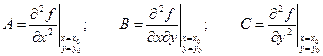
Тесты
2.1. Область определения функции 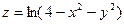 :
:
1) Вся плоскость хОу;
2) 1 и 3 четверти;
3) Круг радиуса 2 с центром в начале координат включая границу;
4) Тот же круг исключая границу.
2.2. 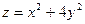 , Линии уровня представляют собой:
, Линии уровня представляют собой:
1) Окружности; 3) гиперболы;
2) Эллипсы; 4) Параболы.
2.3. 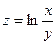 частная производная
частная производная 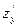 =
=
1) 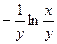 ; 2)
; 2) 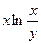 ; 3)
; 3) 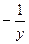 ; 4)
; 4) 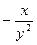 .
.
2.4. 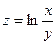 ;
; 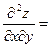
1) 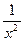 ; 2)
; 2) 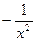 ; 3) 0; 4)
; 3) 0; 4) 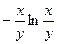 .
.
2.5. 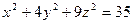 ; Уравнение касательной плоскости, проведенной к заданной поверхности в точке М(1; 2;
; Уравнение касательной плоскости, проведенной к заданной поверхности в точке М(1; 2; 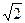 ) имеет вид:
) имеет вид:
1) 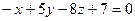 ;
;
2) 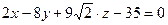 ;
;
3) 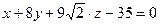 .
.
2.6. 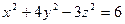 ; Уравнение нормали, проведенной к заданной поверхности в точке N(1; 2; 1) примет вид:
; Уравнение нормали, проведенной к заданной поверхности в точке N(1; 2; 1) примет вид:
1) 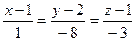 ;
;
2) 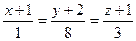 ;
;
3) 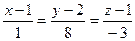 .
.
2.7. Производная функции 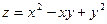 в точке М(1; 1) в направлении вектора
в точке М(1; 1) в направлении вектора 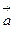 (6; 8) равна:
(6; 8) равна:
1) 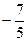 ; 2)
; 2) 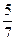 ; 3)
; 3) 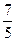 ; 4)
; 4) 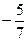 .
.
2.8. Градиент функции 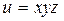 в точке М(2; 1; 1) равен:
в точке М(2; 1; 1) равен:
1) 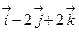 ; 3)
; 3) 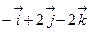 ;
;
2) 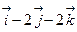 ; 4)
; 4) 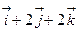 .
.
2.9. Имеет ли функция 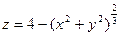 экстремум и, если да, то какой и в какой точке:
экстремум и, если да, то какой и в какой точке:
1) max; (1; 1); 3) max; (0; 0);
2) min; (1; 1); 4) min; (0; 0).
2.10. 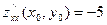 ;
; 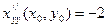 ;
; 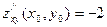 . Функция z в точке
. Функция z в точке 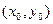 :
:
1) Имеет min; 3) Не имеет экстремума;
2) Имеет max; 4) Неясно.
Интегральное исчисление.
Неопределенный интеграл.
Определение. Таблица интегралов.
Одной из задач предыдущей части курса было нахождение производной функции f(x) -новой функции f `(x). Сформулируем обратную задачу – найти функцию F(x), производная которой - заданная функция f(x).
Функция F(x) называется первообразной функции f(x) на отрезке [a, b], если во всех точках этого отрезка выполняется равенство F`(x) = f(x).
Первообразная определяется с точностью до произвольной постоянной: [F(x) + C]` = f(x). Если F(x) – первообразная функции f(x), то функциями видаF(x) + C исчерпываются все первообразные функции f(x).
Если функция F(х) – первообразная функции f(x), то выражение F(x) + C называется неопределенным интегралом от функции f(x) и обозначается
ò f(x)dx = F(x) + C (5.1),
где . f(x) – подинтегральная функция, f(x)dx – подинтегральное выражение, ò – знак интеграла.
Неопределенный интеграл представляет собой семейство функций, геометрически – семейство кривых, каждая из которых получается сдвигом одной из кривых вдоль оси Оу.
Если функция f(x) непрерывна на отрезке [a, b], то для этой функции существует первообразная (и неопределенный интеграл). (Теорема существования).
Нахождение первообразной функции f(x) называется интегрированием ее.
Отметим, что если производная элементарной функции также элементарная функция, то первообразная элементарной функции может оказаться и неэлементарной функцией.
Из определения первообразной следует:
1. Производная от неопределенного интеграла равна подинтегральной функции, т.е. если F`(x) = f(x), то и (òf(x)dx)` = f(x) (5.2).
2. Дифференциал от неопределенного интеграла равен подинтегральному выражению, т.е. d(òf(x)dx) = f(x)dx (5.3).
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная òF(x) dx = F(x) + C(5.4).
Несложно показать, что справедливы и следующие свойства:
4. Неопределенный интеграл от алгебраической суммы нескольких функций равен сумме интегралов от них: ò[f1(x) + f2(x)]dx = òf1(x)dx + òf2(x)dx(5.5).
5. Постоянный множитель можно выносить за знак интеграла, т.е. если а = const, то òaf(x)dx = aòf(x)dx (5.6).
6. Если òf(x)dx = F(x) + C и u = j(x), то òf(u)du = F(u) + C (5.7).
Используя таблицу производных и соотношения (5.2) – (5.7) несложно получить таблицу интегралов от простейших функций.
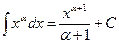 при a ¹ –1 (5.8) при a ¹ –1 (5.8) | 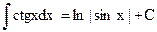 (5.15) (5.15) |
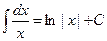 (5.9) (5.9) | 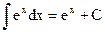 (5.16) (5.16) |
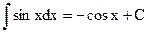 (5.10) (5.10) | 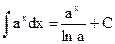 (5.16`) (5.16`) |
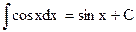 (5.11) (5.11) | 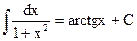 (5.17) (5.17) |
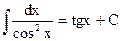 (5.12) (5.12) | 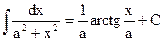 (5.17`) (5.17`) |
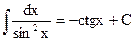 (5.13) (5.13) | 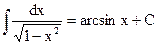 (5.18) (5.18) |
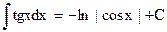 (5.14) (5.14) | 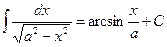 (5.18`) (5.18`) |
Приведем еще две формулы, справедливость которых можно проверить дифференцированием.
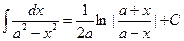 (5.19)
(5.19) 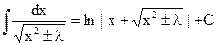 (5.20)
(5.20)
Интегрирование в случаях, когда удается сразу воспользоваться табличными интегралами, называют непосредственным. Чаще подинтегральную функцию приходится преобразовывать, чтобы свести исходный интеграл к одному или нескольким табличным. Один из эффективных приемов – метод подстановки: в интеграле вида òf(x)dxделают замену переменной, положив x = j(t)(j(t) – непрерывная функция с непрерывной производной, имеющая обратную функцию). Тогда dx = j`(t)dt и òf(x)dx = òf(j(t))j`(t)dt. Подразумевается, что после интегрирования в правой части равенства вместо t будет подставлено его выражение через х (возвращение к исходной переменной). Функцию j(t) следует выбирать так, чтобы вычисление интеграла в правой части было максимально простым.
Поясним на примере: 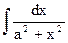 . Положим х = аt, откуда dx = аdt, t=x/a.. Исходный интеграл примет вид
. Положим х = аt, откуда dx = аdt, t=x/a.. Исходный интеграл примет вид 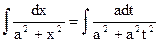 =
= 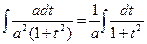 = [см (5.17)] =
= [см (5.17)] = 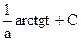 =
= 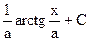 Т.о.
Т.о. 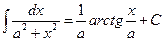 (5.17`).
(5.17`).
Иногда удобнее применять замену переменной вида t = y(x). Вычислим
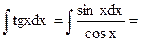 [cosx = t; sinxdx = –dt] =
[cosx = t; sinxdx = –dt] = 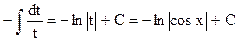 .
.
Интегрирование по частям.Если u и v дифференцируемые функции от х, то d(uv) = vdu + udv откуда, интегрируя, получим
uv = òvdu + òudvиòudv = uv – òvdu (5.22).
Это соотношение называют формулой интегрирования по частям.
Подинтегральное выражение "разбивают на части" - u и dv, подбирая их так, чтобы òvdu был табличным или более простым, чем исходный.
Пример: òхехdx = ?Положим u = x и exdx = dv, тогда du = dx и v = ex откуда òхехdx = хех – òехdx = хех – ех + C.
Отметим, что при нахождении v по dv произвольную постоянную без потери общности полагают равной нулю.
Интегрирование рациональных функции.Всякую рациональную функцию можно представить в виде рациональной дроби – отношения двух многочленов (без потери общности полагаем, что они не имеют общих корней).
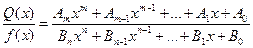
Если степень числителя ниже степени знаменателя дробь называют правильной, в противном случае - неправильной. Неправильную дробь (m ³ n), разделив числитель на знаменатель, можно представить в виде суммы многочлена и правильной дроби 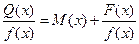 .
.
Рациональные дроби вида: 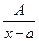 ;
; 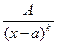 ;
; 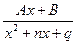 ;
; 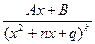 , где k – целое положительное число ³ 2,
, где k – целое положительное число ³ 2, 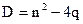 называются простейшими дробями 1, 2, 3 и 4 типов. Всякую правильную рациональную дробь можно представить в виде суммы простейших дробей, интегралы от которых рассмотрены ниже.
называются простейшими дробями 1, 2, 3 и 4 типов. Всякую правильную рациональную дробь можно представить в виде суммы простейших дробей, интегралы от которых рассмотрены ниже.
1. 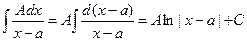 (5.23)
(5.23)
2. 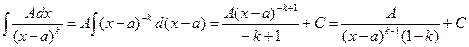 (5.24)
(5.24)
3. 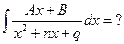 Применим следующий способ. Найдем дифференциал знаменателя d(x2 + nx + q) = (2x + n)dx и представим числитель в виде суммы
Применим следующий способ. Найдем дифференциал знаменателя d(x2 + nx + q) = (2x + n)dx и представим числитель в виде суммы 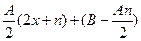 , тогда
, тогда
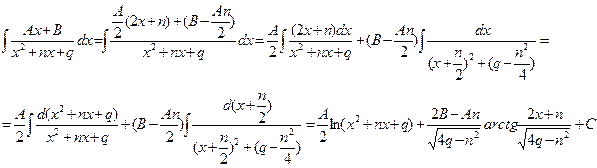 (5.25)
(5.25)
Интеграл от простейшей дроби четвёртого типа легко вычисляется с помощью тригонометрической подстановки и будет рассмотрен ниже.
Разложение рациональной дроби на простейшие можно осуществить опираясь на следующие теоремы (приводятся без доказательств).
1. Если х = а есть корень знаменателя кратности к, т.е. f(x) = (х – а)кf1(x)где f1(а)¹ 0, то правильную дробь 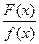 можно представить в виде суммы двух других правильных дробей
можно представить в виде суммы двух других правильных дробей 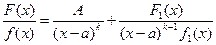 , где А – постоянная, отличная от нуля , а F1(x) многочлен, степень которого ниже степени знаменателя (х – а)к–1f1(x).
, где А – постоянная, отличная от нуля , а F1(x) многочлен, степень которого ниже степени знаменателя (х – а)к–1f1(x).
1. Если f(x) = (x2 + nx + q)mj1(x), где многочлен j1(х) не делится на x2 + nx + q, то правильную рациональную дробь 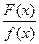 можно представить в виде суммы двух других правильных дробей следующим образом:
можно представить в виде суммы двух других правильных дробей следующим образом: 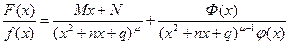 , где Ф(х) – многочлен, степень которого ниже степени многочлена (x2 + nx + q)m–1j(x). Применяя к дроби
, где Ф(х) – многочлен, степень которого ниже степени многочлена (x2 + nx + q)m–1j(x). Применяя к дроби 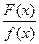 эти теоремы, можно выделить последовательно все простейшие дроби, соответствующие корням знаменателя f(x). Т.е. если f(x) = (х – а)a(х – b)b …(x2 + nx + q)m… (x2 + lx + s)n , то дробь представима в виде:
эти теоремы, можно выделить последовательно все простейшие дроби, соответствующие корням знаменателя f(x). Т.е. если f(x) = (х – а)a(х – b)b …(x2 + nx + q)m… (x2 + lx + s)n , то дробь представима в виде:
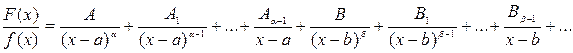
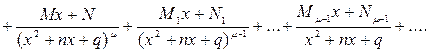
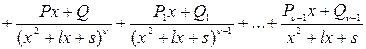
Коэффициенты А, А1, …, В, В1, … определяют исходя из того, что последнее равенство есть тождество. Приведя дроби к общему знаменателю, получим тождественные многочлены в числителях слева и справа. Приравнивая коэффициенты при одинаковых степенях х, получим систему уравнений относительно неизвестных коэффициентов А, А1, …,В, В1, …
Пример: используя предложенный способ разложим на простейшие дроби 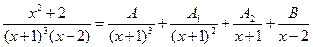 . Приведя слагаемые к общему знаменателю и приравняв числители, получим х2 + 2 = А(х – 2) + А1(х + 1)(х –2)
. Приведя слагаемые к общему знаменателю и приравняв числители, получим х2 + 2 = А(х – 2) + А1(х + 1)(х –2)
+ А2(х + 1)2(х –2) + В(х +1)3 или х2 + 2 = (А2 + В)х3 + (А1 + 3В)х2 + (А – А1 – 3А2 +
+ 3В)х + (–2А – 2А1 – 2А2 + В). Приравнивая коэффициенты при х3, х2, х, и х0 (свободный член) получим систему
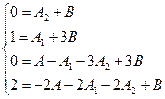 решая которую найдем: А = –1, А1 = 1/3, А2 = – 2/9, В = 2/9
решая которую найдем: А = –1, А1 = 1/3, А2 = – 2/9, В = 2/9
В результате получим: 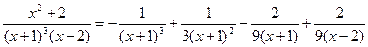 .
.
Чтобы вычислить интеграл от рациональной дроби, нужно, если дробь неправильная, представить ее в виде суммы многочлена и правильной дроби, а дробь разложить на сумму простейших.
Пример: