Метод відокремлення змінних (метод Фур’є) побудови розв’язків змішаних задач для рівнянь параболічного типу

Схема інтеґрування змішаних задач для рівнянь параболічного типу є аналоґічною схемі розв’язування змішаних задач для рівнянь гіперболічного типу (тема ІІІ). Наведемо основні ідеї методу відокремлення змінних побудови розв’язків змішаних задач на прикладі першої змішаної задачі для рівняння поширення тепла в однорідному ізотропному стержні:

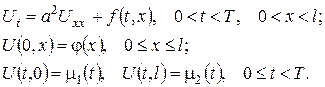
Будемо вважати, що початкова та крайові умови є узгодженими, тобто виконуються рівності , .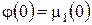

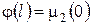Можна вирізнити чотири типи задач.

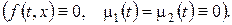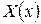1. Задача для однорідного рівняння з однорідними крайовими умовами Розв’язок шукається у вигляді добутку: де – власні функції відповідної задачі Штурма-Ліувілля, а 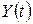визначаються з однорідного рівняння та початкової умови.

2. Задача для неоднорідного рівняння з однорідними крайовими умовами 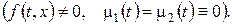Будемо вважати, що 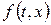як функція змінної х справджує крайові умови. Тоді згідно методу Фур’є розв’язок шукається у вигляді ряду

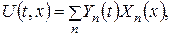
де 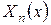– власні функції задачі Штурма-Ліувілля для відповідної однорідної задачі, а 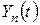визначаються підстановкою ряду для 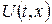у неоднорідне рівняння та в початкову умову.

3. Загальна змішана задача: 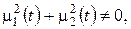тобто хоча б одна з крайових умов неоднорідна. Тоді для застосування методу відокремлення змінних необхідно спершу звести крайові умови до однорідних. Розв’язок шукаємо у вигляді суми 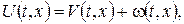причому допоміжну функцію 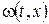підбираємо таким чином, щоб вона справджувала крайові умови. Зокрема, у випадку поставленої вище задачі слід вимагати виконання умов ,

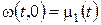- 8 -

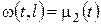. Тоді для нової невідомої функції 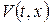одержимо змішану задачу типу 1 або типу 2, до якої за умови її коректної постановки можна застосувати метод Фур’є.

Зауваження. Допоміжну функцію 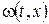зручно шукати в стандартному лінійному вигляді 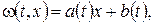де коефіцієнти 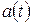і 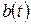визначаються з крайових умов. Зокрема, якщо обидві крайові умови першого роду, то одержимо: 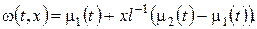Винятком є друга змішана задача: якщо обидві крайові умови другого роду, тобто мають вигляд 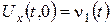, , 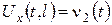то допоміжна функція як лінійна не визначається однозначно,

зате її можна шукати у вигляді 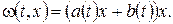У цьому випадку будемо мати 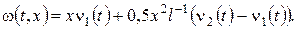Проте такі прості прийоми не завжди є ефективними, адже слід пам’ятати, що до змішаної задачі з однорідними крайовими умовами, яку одержимо для 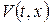, метод Фур’є застосовний лише тоді, коли вільний член у рівнянні справджує крайові умови (за винятком випадку задачі зі стаціонарними неоднорідностями, поданого нижче). Якщо цього домогтися не вдалося, то слід шукати інші способи побудови допоміжної функції.

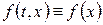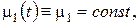
4. Задача зі стаціонарними неоднорідностями: вільний член у рівнянні та крайові умови не залежать від часу, тобто , 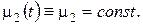Цю задачу можна розв’язувати як загальну змішану задачу (вона є частинним випадком загальної задачі), проте в даному випадку це нераціонально. Найзручніше шукати розв’язок у вигляді

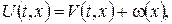
де допоміжна функція 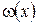(стаціонарна температура) повинна справджувати не лише крайові умови, а й рівняння. Зокрема, для поставленої вище змішаної задачі 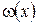повинна бути розв’язком наступної крайової задачі:

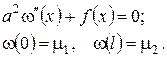
Тоді для функції 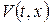одержимо змішану задачу типу 1 (однорідне рівняння та однорідні крайові умови), до якої безумовно застосовний метод Фур’є.