Метод Ньютона
Минимизация двумерных функций
Метод Гаусса Зайделя
Метод покоординатного спуска
Функцию цели обозначим как 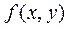
Алгоритм метода:
Шаг 1. Задать стартовую точку ( 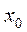 ,
, 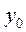 ), точность решения
), точность решения 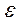 ,
, 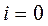 .
.
Шаг 2. Минимизация одномерной функции 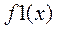 , полученной из функции
, полученной из функции 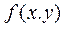 :
: 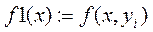 . Стартуем из точки
. Стартуем из точки 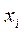 .
.
Пусть минимум получен в точке 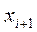 .
.
Шаг 3. Минимизация одномерной функции 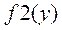 , полученной из функции
, полученной из функции 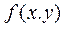 :
: 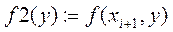 . Стартуем из точки
. Стартуем из точки 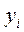 .
.
Пусть минимум получен в точке 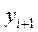 .
.
Шаг 4. Улучшено ли ранее полученное решение?
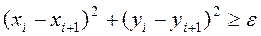 (1)
(1)
Если (1) верно, 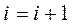 , идти на Шаг 2.
, идти на Шаг 2.
Если (1) не верно, решением является ( 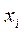 ,
, 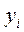 ). Останов.
). Останов.
Минимизация двумерных функций
Метод Ньютона
Функцию цели обозначим как 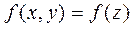 ,
, 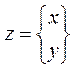 .
.
Алгоритм метода:
Шаг 1. Задать стартовую точку 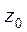 , точность решения
, точность решения 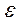 ,
, 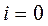 .
.
Шаг 2. Новая точка получается как 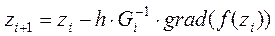 , где
, где
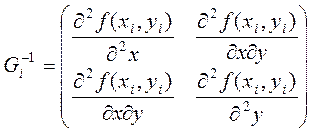 ,
, 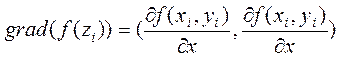
Шаг 3. Улучшено ли ранее полученное решение?
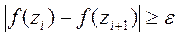 (1)
(1)
Если (1) верно, 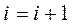 , идти на Шаг 2.
, идти на Шаг 2.
Если (1) не верно, решением является 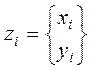 . Останов.
. Останов.
