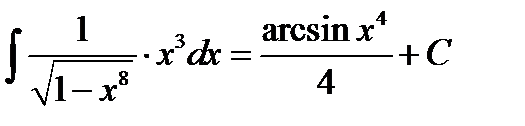Второе правило замены переменной
Тема. Вычисление первообразных. Метод замены переменной в подынтегральном выражении.
Занятие 5.
Рассмотрим дифференциал функции 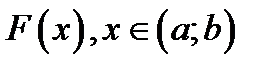 :
: 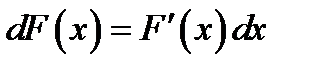 . Если
. Если 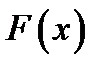 является первообразной для функции
является первообразной для функции 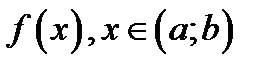 , то
, то 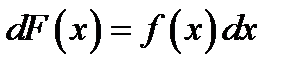 . Первообразная функция
. Первообразная функция 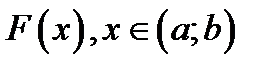 для функции
для функции 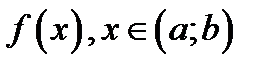 обозначается символом
обозначается символом 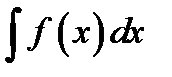 . Операция нахождения первообразной называется неопределённым интегрированием. Следующие записи эквивалентны
. Операция нахождения первообразной называется неопределённым интегрированием. Следующие записи эквивалентны
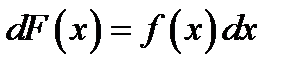
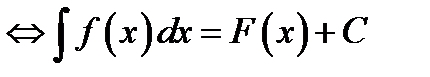 . (5.1)
. (5.1)
При вычислении неопределённого интеграла используются свойства:
1) 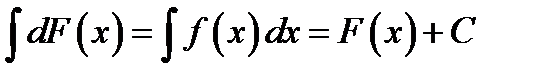 .
.
2) инвариантности интегрирования:
Если 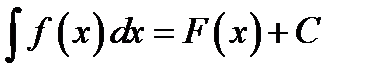 , то
, то 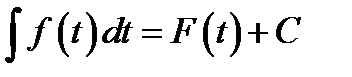 ,где
,где  любая дифференцируемая переменная, а также правила интегрирования:
любая дифференцируемая переменная, а также правила интегрирования:
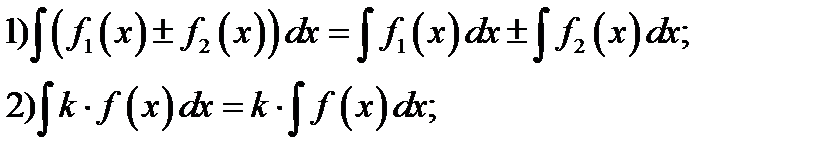 (5.2)
(5.2)
Для проверки правильности полученного результата используют свойство
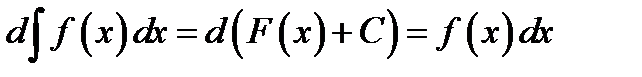 (5.3)
(5.3)
Пример 1.Проверим правильность формул
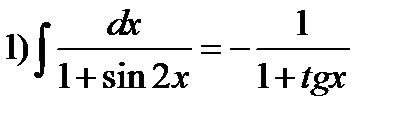 ;
; 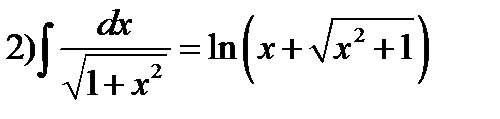 ;
;
Решение. Используем свойство (5.1)
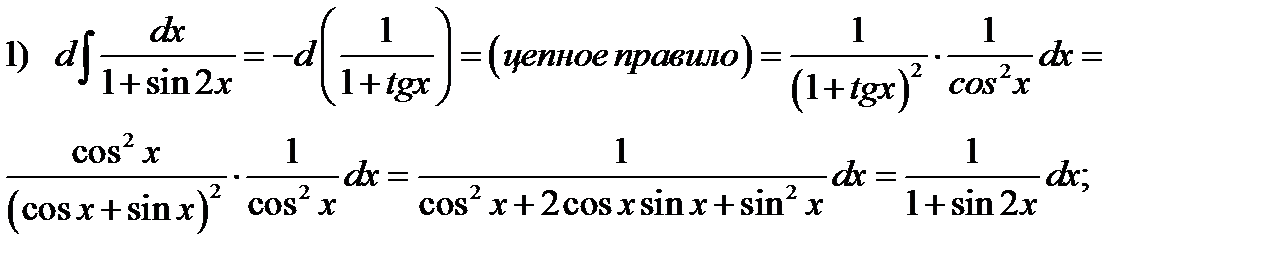
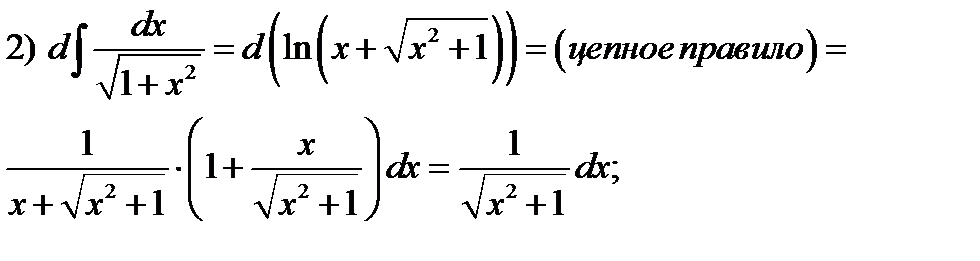
Свойства (5.1),(5.3) показывают нам, что операции дифференцирования и неопределённого интегрирования являются взаимно обратными с точностью до произвольной постоянной.
Практически любой метод неопределённого интегрирования заключается в следующем. Используя свойства и правила интегрирования, мы преобразуем интеграл к известному табличному интегралу.
Существует три основных метода интегрирования 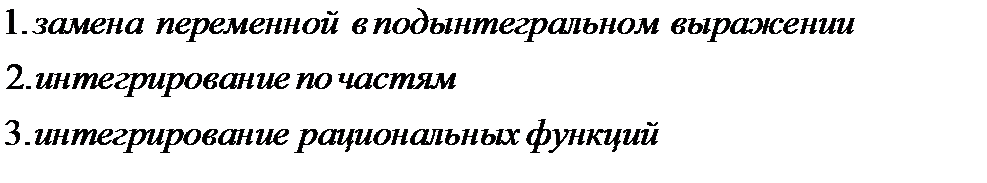
Метод замены переменной интегрирования в неопределённом интеграле
Постановка задачи. Пусть задана функция 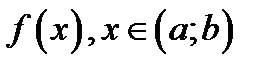 . Требуется найти первообразную функцию
. Требуется найти первообразную функцию 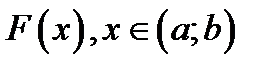 такую, что
такую, что 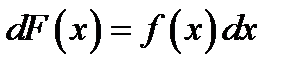 .
.
Первое правило замены переменной. Прямая замена. Требуется найти 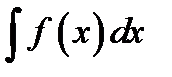 .
.
Заменяем переменную интегрирования по правилу 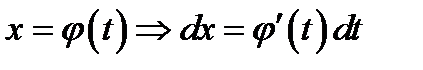 .
.
Имеем 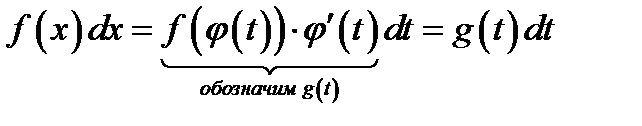 . Допустим , что замена
. Допустим , что замена 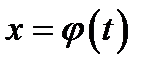 такова,
такова,
что неопределённый интеграл 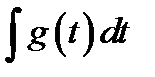 известен и равен
известен и равен 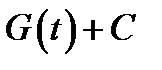 , то есть
, то есть 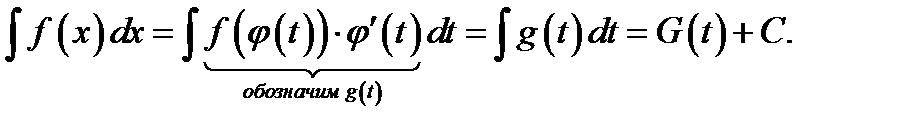
Обращая равенство 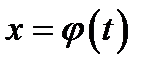 , получаем
, получаем 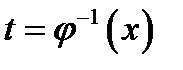 и записываем ответ
и записываем ответ 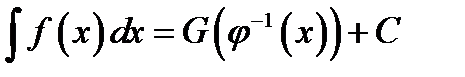 .
.
Пример 2.Найти первообразные функции 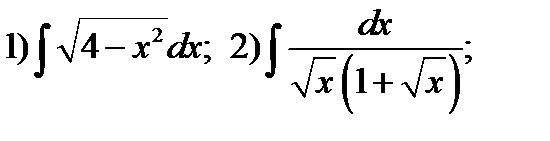
Решение. Решаем 1). Чтобы подынтегральное выражение упростилось , положим 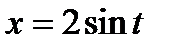 .
.
Тогда
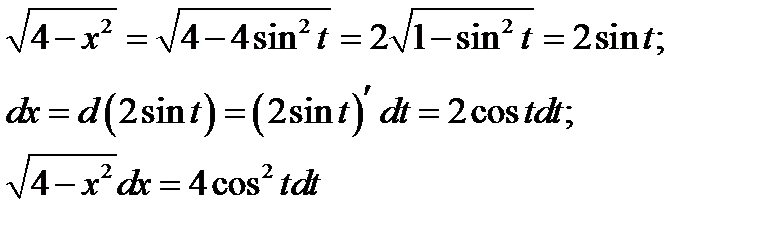
Таким образом
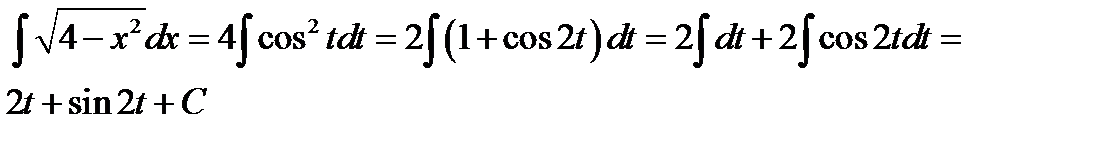

Чтобы получить ответ нужно вернуться от переменной 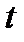 к старой переменной
к старой переменной 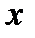
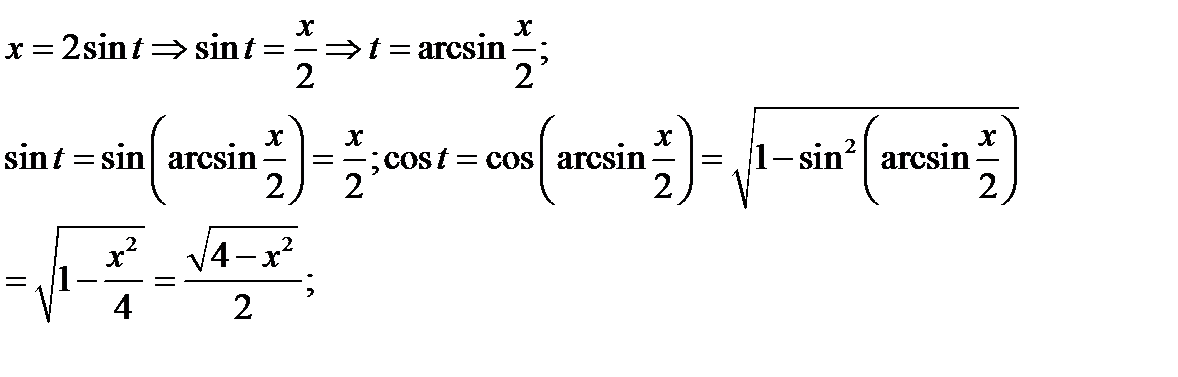
Откуда 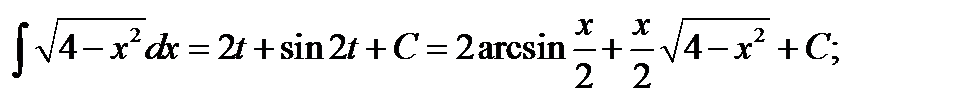
Проверка полученного результата 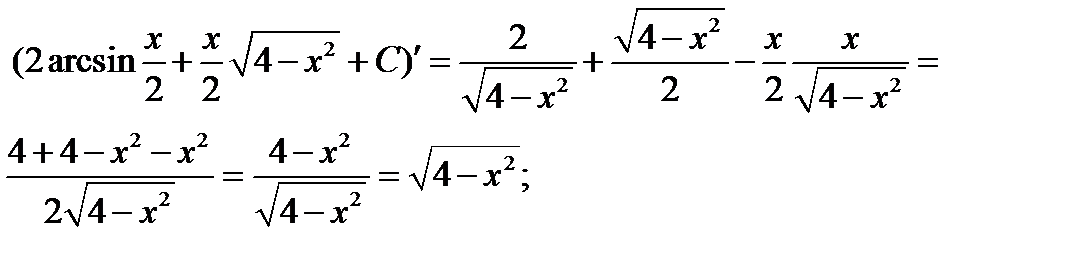
Или 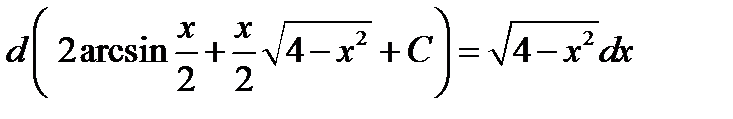 ;
;
Решаем 2) . Чтобы подынтегральное выражение упростилось, положим 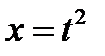 .
.
Тогда
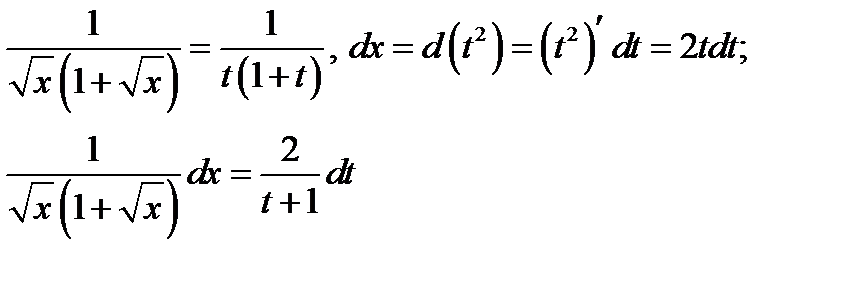
Таким образом
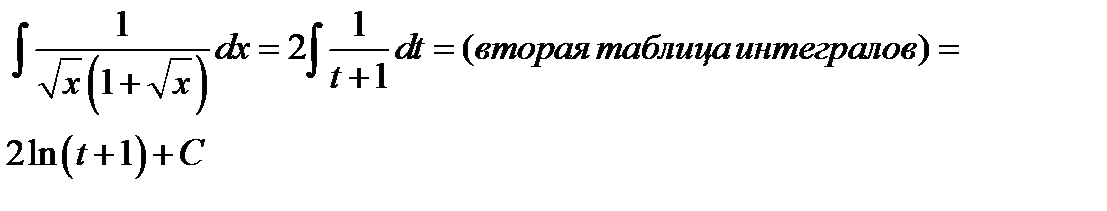

Чтобы получить ответ нужно вернуться от переменной 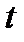 к старой переменной
к старой переменной 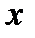
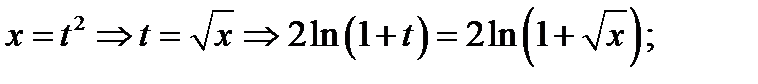
Откуда 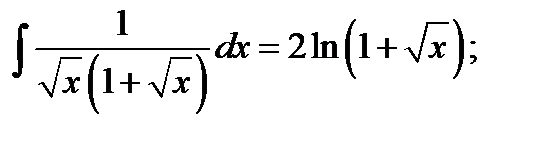
Проверка полученного результата
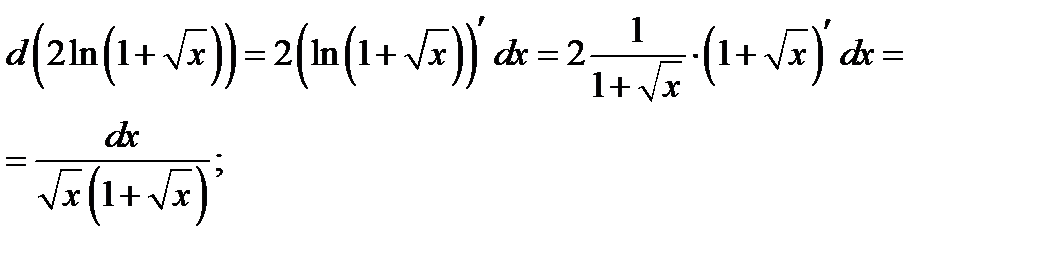
Второе правило замены переменной.
Пусть требуется вычислить интеграл 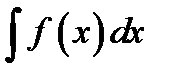 . Если можно разложить подынтегральную функцию
. Если можно разложить подынтегральную функцию 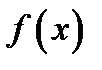 на два множителя
на два множителя 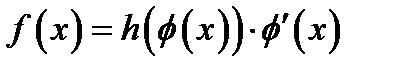 , то
, то
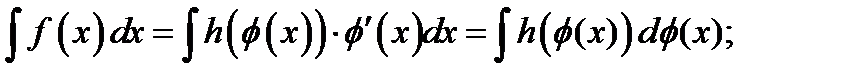
Если известно, что 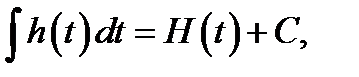 то
то
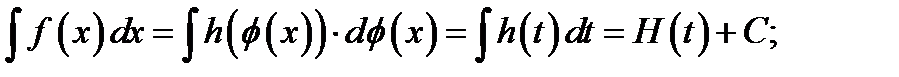
Чтобы получить ответ нужно вернуться от переменной 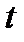 к старой переменной
к старой переменной 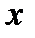
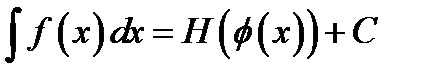 .
.
Пример 3.Найти неопределённые интегралы
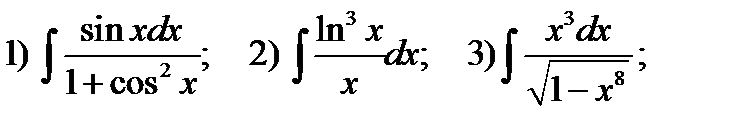
Решение. Решаем 1). Разлагаем подынтегральную функцию 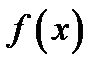 на два сомножителя
на два сомножителя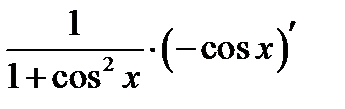 .Тогда подынтегральное выражениебудет равно
.Тогда подынтегральное выражениебудет равно
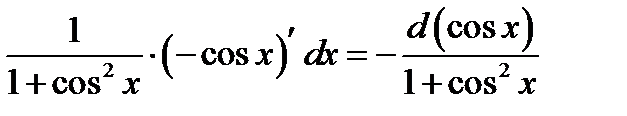 .Производим замену переменной по правилу
.Производим замену переменной по правилу 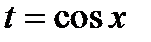
и в результате получаем 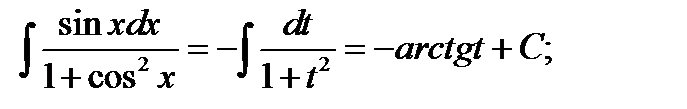
возвращаясь к старой переменной, записываем ответ 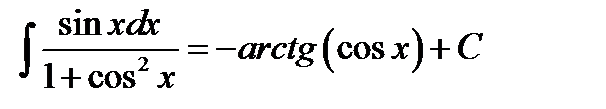
Проверка полученного результата : 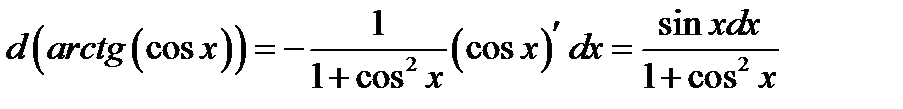
Решаем 2). Разлагаем подынтегральную функцию 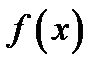 на два сомножителя
на два сомножителя 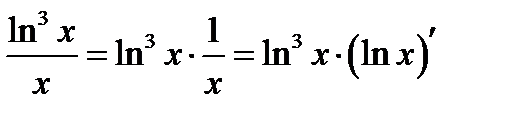 .Тогда подынтегральное выражениебудет равно
.Тогда подынтегральное выражениебудет равно
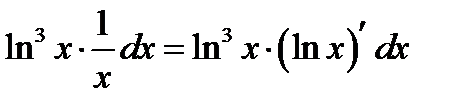 .Производим замену переменной по правилу
.Производим замену переменной по правилу 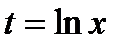
и в результате получаем 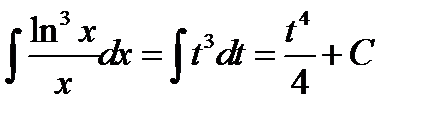 ;
;
Возвращаясь к старой переменной, записываем ответ 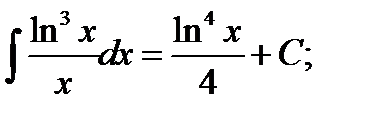
Решаем 2). Разлагаем подынтегральную функцию 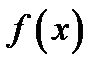 на два сомножителя
на два сомножителя 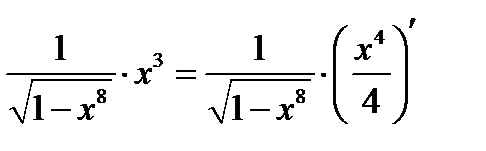 .Тогда подынтегральное выражениебудет равно
.Тогда подынтегральное выражениебудет равно
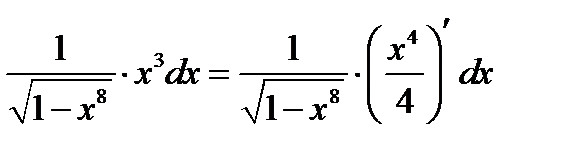 .Производим замену переменной по правилу
.Производим замену переменной по правилу 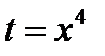
и в результате получаем 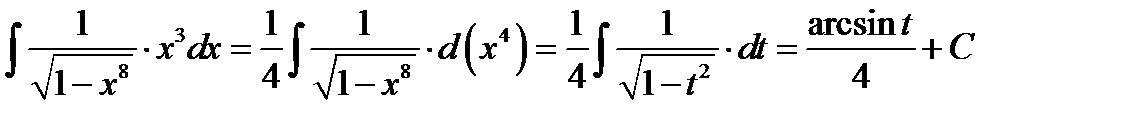 ;
;
Возвращаясь к старой переменной, записываем ответ