Дифференциальные уравнения первого порядка. Министерство образования и науки

Министерство образования и науки

Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

Национальный исследовательский ядерный университет «МИФИ»

Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

РЯДЫ

Методические указания к решению контрольных работ студентов-заочников

Волгодонск

УДК 517.9 (076.5)

Рецензент д-р. техн. наук В.В.Кривин

Составители: Сысоев Ю.С., Столяр Л.Н.

Дифференциальные уравнения. Ряды: Методические указания к решению контрольных работ студентов-заочников

Предлагаемые методические указания содержат подробные решения типовых задач и задачи для самостоятельного решения, снабженные ответами и указаниями.

Методические указания предназначены для студентов-заочников и могут быть использованы как руководство при выполнении контрольных работ по соответствующим темам.

Оглавление

ВВЕДЕНИЕ 3

1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 5

1.1Дифференциальные уравнения первого порядка 5

1.2 Дифференциальные уравнения второго порядка,

допускающие понижение порядка 12

1.3 Линейные однородные и неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 15

1.3.1 Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами 15

1.3.2 Линейные неоднородные дифференциальные урав- нения второго порядка с постоянными коэффициентами 16

1.4 Системы линейных дифференциальных уравнений с постоянными коэффициентами 23

2. РЯДЫ 27

2.1 Числовые ряды 27

2.2 Функциональные ряды 32

Контрольная работа на тему:

«Дифференциальные уравнения» 36

Контрольная работа на тему: «Ряды» 39

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 41

ВВЕДЕНИЕ

Представленные методические указания содержат подробные решения задач по темам: дифференциальные уравнения и ряды, сопровождаемые необходимыми теоретическими и методическими указаниями. По каждой теме приведены задания для самостоятельной работы с ответами. В заключении приведен текст контрольных работ по темам: дифференциальные уравнения и ряды для студентов-заочников всех направлений, по которым ведется обучение в Волгодонском инженерно-техническом институте (филиале НИЯУ МИФИ). Каждая контрольная работа состоит из четырех заданий. Студенту необходимо выполнить из каждого задания один номер, который соответствует его варианту.

Выбор вариантов контрольных работ производится по последней цифре номера зачетной книжки. Например, если последняя цифра равна 5, то выполняется вариант № 5, следовательно, из каждого задания решается задача под номером 5. Если последняя цифра равна 0, то из каждого задания решается задача под номером 10.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Дифференциальные уравнения первого порядка

Дифференциальными уравнениями первого порядка называются уравнения вида 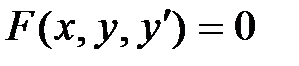. [1, гл. X, §1].

Чаще мы будем рассматривать уравнения, разрешенные относительно первой производной, т.е. уравнения вида: 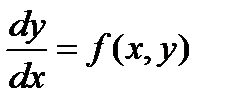. Во многих случаях оказывается целесообразным вместо этого уравнения рассматривать дифференциальное уравнение

.

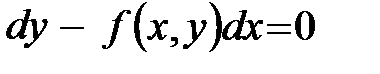Умножая обе части этого уравнения на некоторую функцию 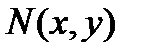, получим:

,

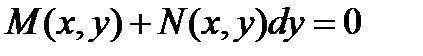где .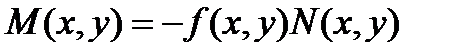

Обе переменные x и y входят в это уравнение равноправно и, если за независимую переменную принять у (что иногда бывает полезно), то уравнение имеет вид: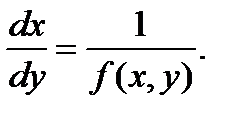

Определение. Решением дифференциального уравнения называется всякая функция 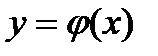, которая, будучи подставлена в уравнение, превращает его в тождество.

Определение. Общим решением дифференциального уравнения первого порядка называется функция 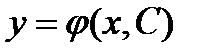, которая является решением при каждом фиксированном С из некоторого множества М, и для любого решения 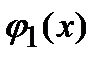существует такое значение С₁ из М, что 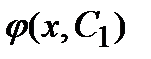= 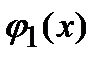при любом х, т.е. любое решение получается из 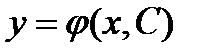выбором соответствующего С.

Перечислим основные типы уравнений и укажем способы их решения:

1) дифференциальное уравнение первого порядка с разделяющимися переменными- это уравнение вида:

.

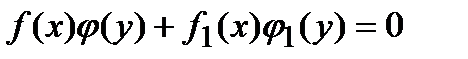Решается это уравнение делением его обеих частей на 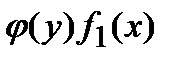и затем интегрированием;

2) однородное дифференциальное уравнение. Функция 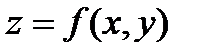, называемая однородной степени 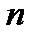, если для любого 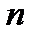выполняется условие: .

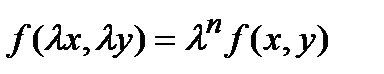Дифференциальное уравнение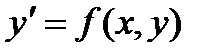

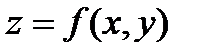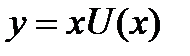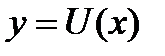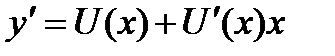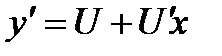называется однородным, если функция - однородная нулевой степени. Такое уравнение заменой , где - новая неизвестная функция, сводится к уравнению с разделяющимися переменными. Действительно, , или (здесь мы не пишем аргумент у функции 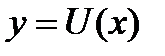, но подразумеваем, что 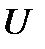является функцией от ).

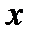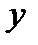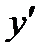Подставляя значение и в уравнение (1), получим:

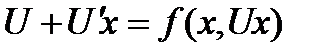, или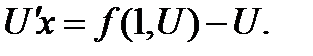

Последнее уравнение является уравнением с разделяющимися переменными. Решив его, найдем функцию 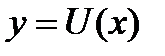, а затем и функцию ;

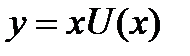3) линейное уравнение. Дифференциальное уравнение вида

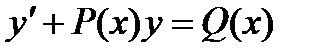(2)

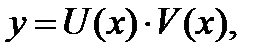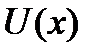называется линейным дифференциальным уравнением первого порядка. Оно сводится к двум уравнениям с разделяющимися переменными подстановкой: где и 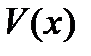- новые неизвестные функции. Действительно, 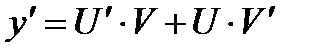, подставляя вместо 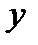и 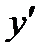их значения в уравнение (2), получим:

.

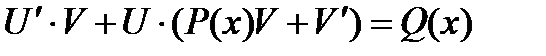Определяя 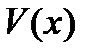из условия, 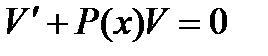находим затем 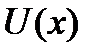из равенства 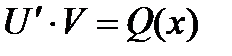. В качестве 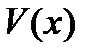можно взять любое частное решение уравнения .

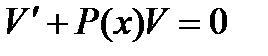4) уравнение Бернулли. Это дифференциальное уравнение вида:

.

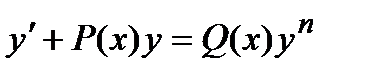Решается оно так же, как и линейное уравнение, подстановкой 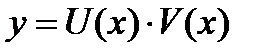или предварительным сведением его к линейному заменой .

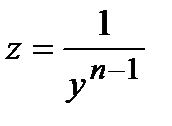Задача 1. Найти общее решение дифференциального уравнения .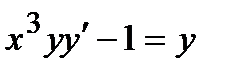

Решение. Преобразуем наше уравнение следующим образом:

; .

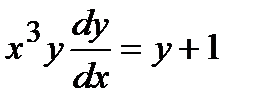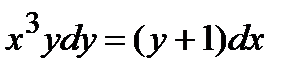Это уравнение с разделяющимися переменными. Разделив обе части последнего равенства на 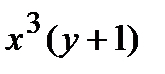получим:

;

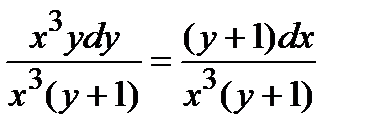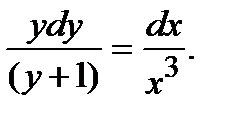
Интегрируя обе части уравнения, получим:

; ;

;

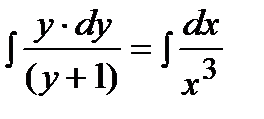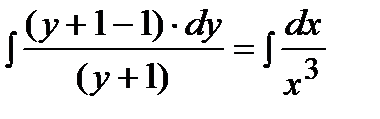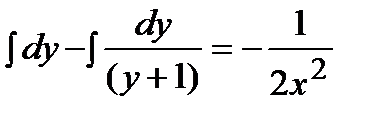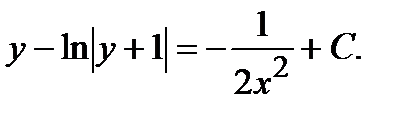
Последнее равенство задает нам решение в виде неявной функции 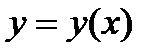. Обратим внимание на то что, что не все решения задаются указанным равенством. При делении на 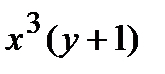могли быть потеряны решения 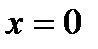и 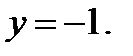Очевидно (подставьте в уравнение), что 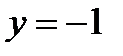является решением, а 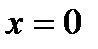– нет. Итак, общее решение задается двумя формулам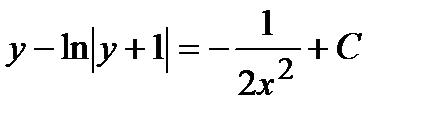и: и .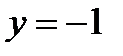

Задача 2. Найти общее решение дифференциального уравнения .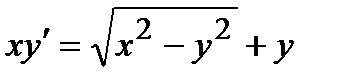

Решение. Преобразуем уравнение к следующему виду:

; .

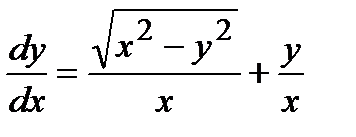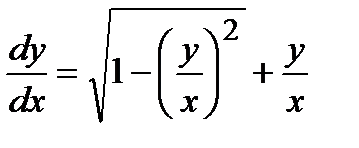Если правую часть последнего уравнения обозначить через 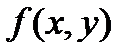, то

= = =

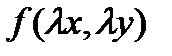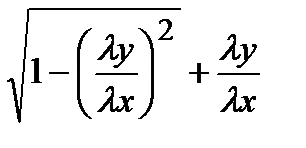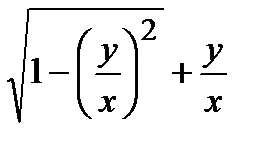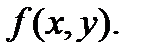
Следовательно, рассматриваемое уравнение является однородным.

Положим теперь 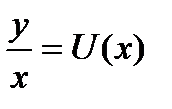, или 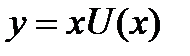,тогда 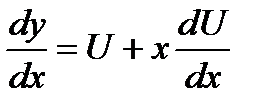. Подставляя в уравнение выражения для у и 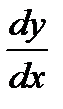, получим: ; ;

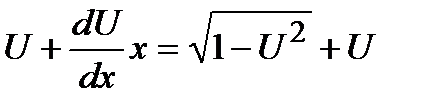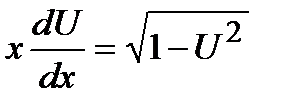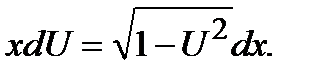
Разделяем переменные в последнем уравнении, деля его на 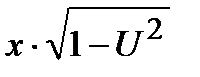, и интегрируем полученное равенство:

;

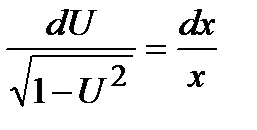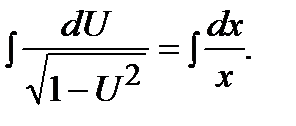
Отсюда 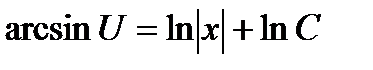, или .

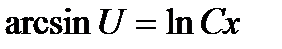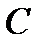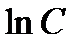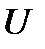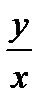Здесь мы вместо константы для удобства добавили константу . Заменяя на , получим решение:

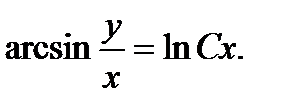
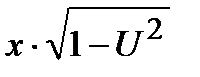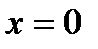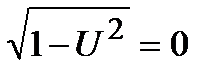Последнее равенство может давать не все решения, часть из них могли потеряться при разделении переменных (мы делили уравнение на ). Положим теперь и . Но 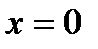не является решением уравнения, а из равенства 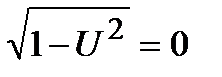получаем, что 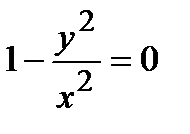, или 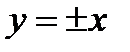. Непосредственной подстановкой в уравнение убеждаемся, что функции 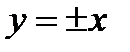являются решениями. В нашем случае все решения задаются тремя формулам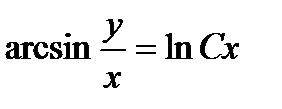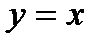и:

; и .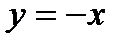

Задача 3. Найти общее решение линейного дифференциального уравнения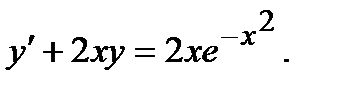

Решение. Это линейное уравнение, поэтому его общее решение будем искать в виде 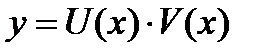. Тогда

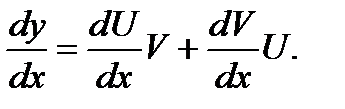
Подставляя у и 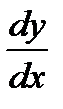в уравнение, получим:

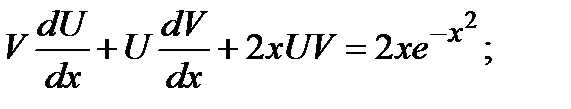
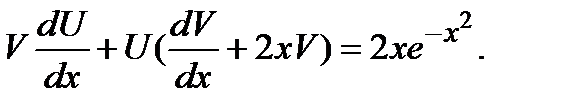
Функцию 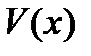найдем из того условия, что выражение в скобке в последнем равенстве должно обращаться в ноль:

.

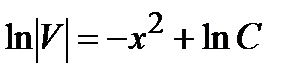Последнее уравнение неявно задает две серии функций:

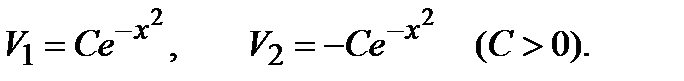
Так как нам достаточно взять какое-то частное решение, то положим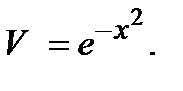

В этом случае наше уравнение перепишется так:

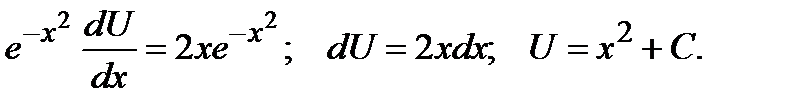
Учитывая, что 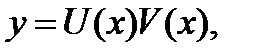получим общее решение уравнения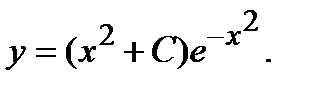

Задача 4. Найти общее решение уравнения Бернулли .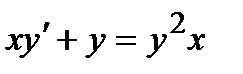

Решение. Положим 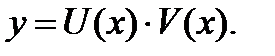Тогда

.

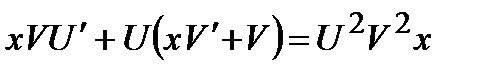Функцию 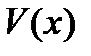найдем как частное решение уравнения 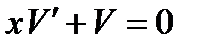. Имеем 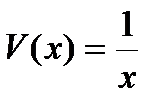. Тогда 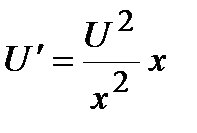, откуда, разделяя переменные и интегрируя, получим:

; ; ;
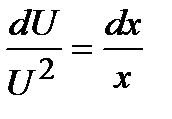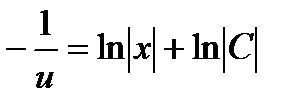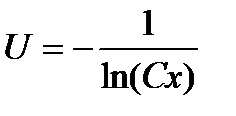