Void approks_analit_funkc_polinomom(int n, int m, float x1, float
2. ввести значение переменной n – степень аппроксимирующего полинома
3. описать массив:
float q[n+1]; // вектор коэффициентов
// аппроксимирующего полинома
// по возрастающим степеням
4. ввести значения переменных x1 и x2 – левая и правая границы аппроксимации,
5. ввести значение переменной m – количество узлов аппроксимации, (m>n),
6. создать функцию float function(float x) , в которой описать аппроксимируемую функцию как f=f(x),например:
Float function(float x)
{
Float f;
f=sqrt(exp(x)+exp(-x));
Return f;
}
7. обратиться к программе вычислений коэффициентов аппроксимирующего полинома:
approks_analit_funkc_polinomom(n, m, x1, x2, q, &s0);
8. вывести на экран терминала (в текстовый файл) вектор коэффициентов q[n+1] и среднеквадратическую погрешность аппроксимации s0.
Пример: аппроксимировать кубическим полиномом функцию:
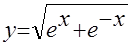
В этом случае n=3, m=11, x1=0.0, x2=1.0.
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
void approks_analit_funkc_polinomom(int n, int m, float x1, float x2, float q[n+1], float *s0);
int main(int argc, char **argv)
{
int n;// степень аппроксимирующего полинома,
int m;// количество узлов аппроксимации,m>n
float x1, x2;// границы аппроксимации
float s0;// среднеквадратическая погрешность
int i;// рабочая переменная
Char c0;
printf("\nApproksimacija polinomom\n");
printf("\nSteprn approks. polinoma n = ");
scanf("%d", &n);
float q[n+1];// массив коэффициентов
// аппроксимирующего полинома
// по возрастанию степеней
printf("\nLevaja granica approks. x1 = ");
scanf("%f", &x1);
printf("\nPravaja granica approks. x2 = ");
scanf("%f", &x2);
printf("\nUzlov approksimacii (m>n) m= ");
scanf("%d", &m);
approks_analit_funkc_polinomom(n, m, x1, x2, q, &s0);
printf("\nKoefficienty approks. polinoma po vozrast. stepeney:\n");
for (i=0; i<n+1; i++)
printf("%10.5f", q[i]);
printf("\n");
printf("\nSrednekvadr. pogreshn. approksimacii: %e\n", s0);
printf("\n");
c0=getch();
Return 0;
}
Описание аппроксимируемой функции:
Float function(float x)
{
Float f;
f=sqrt(exp(x)+exp(-x));
Return f;
}
Результат работы программы:
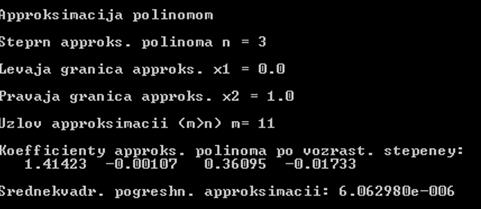
Таким образом, аппроксимирующий полином имеет вид:
f(x)=1,4142 – 0,0011 x + 0,361 x2 – 0,017 x3
Аппроксимация функций, заданных аналитически,
многочленами Чебышева
В головной программе необходимо:
1. описать прототип функции:
void approks_Chebyshev(int n, float x1, float x2, float q[n+1], float cheb[n+1], float r[n+1][n+1], float *eps);
2. ввести значение переменной n – степень аппроксимирующего полинома,
3. описать массивы:
float q[n+1]; // вектор коэффициентов
// аппроксимирующего полинома
// по возрастающим степеням
float cheb[n+1]; // массив коэффициентов
// при аппроксимирующих многочленах Чебышева
float r[n+1][n+1]; // массив коэффициентов
// многочленов Чебышева
4. ввести значения переменных x1 и x2 – левая и правая границы аппроксимации,
5. создать функцию float function(float x) , в которой описать аппроксимируемую функцию как f=f(x),например:
Float function(float x)
//
// Описание аппроксимируемой функции в виде f=f(x)
//
{
Float f;
f=log(x);
Return f;
}
6. обратиться к программе вычислений коэффициентов аппроксимирующего полинома:
approks_Chebyshev(n, x1, x2, q, cheb, r, &eps);
7. вывести на экран терминала (в текстовый файл) векторы коэффициентов q[n+1] и cheb[n+1],массивr[n+1][n+1]иабсолютную погрешность аппроксимации eps в средине интервала.
Пример: аппроксимировать кубическим полиномом функцию:
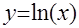
на интервале от x1=1,0 до x2=2,0.
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
void approks_Chebyshev(int n, float x1, float x2, float q[n+1], float cheb[n+1], float r[n+1][n+1], float *eps);
int main(int argc, char **argv)
{
int n;// степень аппроксимирующего полинома
float x1, x2;// границы интервала аппроксимации
float eps;// абсолютная погрешность аппроксимации
// в середине заданного интервала (x1, x2)
int i, j;// рабочие переменные
printf("\n stepen approks. polinoma n = ");
scanf("%d", &n);
float q[n+1];// массив коэффициентов
// аппроксимирующего полинома
// по возрастанию степеней
float cheb[n+1];// массив коэффициентов при
// аппроксимирующих многочленах Чебышева
float r[n+1][n+1];// массив коэффициентов
// многочленов Чебышева
printf("\n levaja granica approks. x1 = ");
scanf("%f", &x1);
printf("\n pravaja granica approks. x2 = ");
scanf("%f", &x2);
approks_Chebyshev(n, x1, x2, q, cheb, r, &eps);
printf("\nKoefficienty approks. polinoma:\n");
for (i=0; i<n+1; i++)
printf("%12.6f", q[i]);
printf("\n");
printf("\nKoefficienty chebyshev. approksim.:\n");
for (i=0; i<n+1; i++)
printf("%12.6f", cheb[i]);
printf("\n");
printf("\nKoefficienty mnogochlenov chebysheva:\n");
for (i=0; i<n+1; i++)
{
for (j=0; j<n+1; j++)
printf("%10.2f", r[i][j]);
printf("\n");
}
printf("\n");
printf("\nAbsoljutnaja pogreshn. approksimacii: %e\n", eps);
Return 0;
}
Описание аппроксимируемой функции:
Float function(float x)
//
// Описание аппроксимируемой функции в виде f=f(x)
//
{
Float f;
f=log(x);
Return f;
}
Результат работы программы:
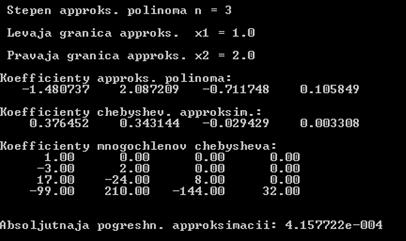
Таким образом, аппроксимирующий полином имеет вид:
f(x)=-1,481 + 2,087 x - 0,712 x2 + 0,106 x3
Чебышевская аппроксимация:
T(x)=0,376 + 0,343 T1(x) – 0,029 T2(x) + 0,0033 T3(x)
Аппроксимация табличных функций сплайн-функциями
В головной программе необходимо:
1. описать прототип функции:
void spline(int n, float x[n], float y[n], float r[n][3], float s[n-1][4]);
2. ввести значение переменной n – количество узлов аппроксимации,
3. описать массивы:
float x[n], y[n]; // значения аргумента и функции
// в узлах аппроксимации
float r[n][3], s[n-1][4];//массивы коэффициентов
// аппроксимирующего кубического сплайна
// по возрастанию степеней
// при двух его представлениях
4. ввести массивы x[n], y[n],
5. обратиться к программе вычислений коэффициентов сплайн-полинома:
Spline(n, x, y, r, s);
6. вывести на экран терминала (в текстовый файл) массив s[n-1][4].
Пример: аппроксимировать кубическим сплайн-полиномом функцию, заданную таблицей ее значений:
| x | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
| y | 2.5 | 0.75 | -1.15 | -2.75 | -3.85 | -4.15 |
В этом случаеn=6.
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
void spline(int n, float x[n], float y[n], float r[n][3], float s[n-1][4]);
int main(int argc, char **argv)
{
int n;// количество узлов аппроксимации
int i, j;// рабочие переменные для ввода исходных данных
Char c0;
printf("\nUzlov approksimacii n= ");
scanf("%d", &n);
float x[n], y[n];// исходные узлы аппроксимации
float r[n][3], s[n-1][4];// массивы коэффициентов
// аппроксимирующего кубического сплайна
// по возрастанию степеней
printf("\nVvedite vector argumenta (%d znacheniy):\n", n);
for (i=0; i<n; i++)
scanf("%f", &x[i]);
printf("\n");
printf("\nVvedite vector funkcii (%d znacheniy):\n", n);
for (i=0; i<n; i++)
scanf("%f", &y[i]);
printf("\n");
printf("\nApproksimacija kubicheskimi splajnami\n");
Spline(n, x, y, r, s);
printf("\nApproksimir. kubich. splajny\n");
printf("\nUchastok\t\tkoefficienty approks. splajna\n");
for (i=0; i<n-1; i++)
{
printf("\n %d\t\t", i+1);
for (j=0; j<4; j++)
printf("%10.5f", s[i][j]);
}
printf("\n");
c0=getch();
Return 0;
}
Результат работы программы:
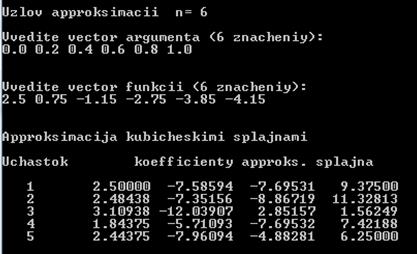
Таким образом, аппроксимирующий сплайн имеет вид:
| Номер участка | Вид полинома |
| 2,5 - 7,586 x – 7,69 5x2 + 9,375 x3 | |
| 2,484 - 7,352 x – 8,867 x2 + 11,328 x3 | |
| 3,109 – 12,039 x + 2,852 x2 + 1,562 x3 | |
| 1,844 – 5,711 x – 7,695 x2 + 7,422 x3 | |
| 2,444 - 7,961 x – 4,883 x2 + 6,25 x3 |
Аппроксимация дробно-рациональной функции
понижением степеней ее числителя и знаменателя
В головной программе необходимо:
- описать прототип аппроксимирующей функции:
int approks_drobi(int l, int m, int n, float q[2][l+1]);
- ввести значение переменной l – степень полинома знаменателя исходной функции,
- ввести значение переменной n – требуемая степень полинома знаменателя (n<l),
- ввести значение переменной m – требуемая степень полинома числителя (m=nилиm=n-1),
- описать массив q[2][l+1] –массив коэффициентов числителя и знаменателя исходной дроби по возрастающим степеням: первая строка – числителя, вторая – знаменателя; после вычислений – массив коэффициентов аппроксимирующей дроби,
- ввести массив q[2][l+1],
- обратиться к программе вычислений:
result = approks_drobi(l, m, n, q);
- вывести на экран терминала (в текстовый файл) вычисленный массив коэфициентов q[2][l+1].
Пример:понизить степень числителя и знаменателя данной функции на единицу:
f(x) = (1 – x) / (1 – 5x + 6x2)
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
int approks_drobi(int l, int m, int n, float q[2][l+1]);
int main(int argc, char **argv)
{
int l;// степень полинома знаменателя исходной дроби
int n;// требуемая степень полинома знаменателя (n<l)
int m;// требуемая степень полинома числителя
// (m=n или m=n-1)
int i, rezult;// рабочие переменные
Char c;
printf("\n l=");
scanf("%d", &l);
printf("\n m=");
scanf("%d", &m);
printf("\n n=");
scanf("%d", &n);
float q[2][l+1];// массив коэффициентов числителя и
// знаменателя исходной дроби
// по возрастающим степеням
// ввод исходного массива
printf("\n Koeff. chislit. ishodn. drobi:\n");
for (i=0; i<=l; i++)
scanf("%f", &q[0][i]);
printf("\n");
printf("\n Koeff. znamenat. ishodn. drobi:\n");
for (i=0; i<=l; i++)
scanf("%f", &q[1][i]);
printf("\n");
rezult=approks_drobi(l, m, n, q);
if(rezult==0)// нормальное завершение
{
printf("\n Koeff. chislit. approks. drobi:\n");
for (i=0; i<=m; i++)
printf("%12.6f", q[0][i]);
printf("\n");
printf("\n Koeff. znamenat. approks. drobi:\n");
for (i=0; i<=n; i++)
printf("%12.6f", q[1][i]);
printf("\n");
}
else printf("\n Reshenija net!\n");
c=getch();
Return 0;
}
Результат решения задачи:
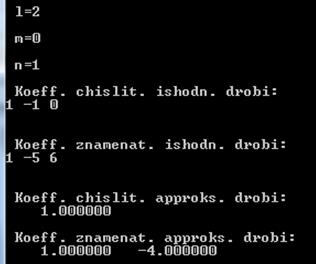
Таким образом, аппроксимирующая дробь имеет вид:
fappr(x) = 1 / (1 – 4x)
Приведение квадратной матрицы к форме Гессенбергера
и вычисление ее собственных значений
В головной программе необходимо:
1. описать прототип функции вычисления корней:
int gessenberger(int n, float a[n][n], float p[2][n]);
2. ввести значение переменной n – размер исходной матрицы,
3. описать массивы:
float a[n][n]; // исходная матрица
float p[2][n]; // массив ее собственных значений:
// первая строка – действительные части,
// вторая строка – мнимые части,
4. ввести исходную матрицу a[n][n],
5. обратиться к программе вычисления собственных значений:
rezult=gessenberger(n, a, p);
6. вывести на экран терминала (в текстовый файл) массив собственных значений
Пример: определить собственные значения матрицы для n=4:
-1.44 1.0 0.62 0.02
a[4][4]= -15.5 -2.1 12.0 0.59
0.0 0.0 0.0 1.0
-4.6 4.84 -531.0 -2.92
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
int gessenberger(int n, float a[n][n], float p[2][n]);
int main(int argc, char **argv)
{
int n;// размер исходной матрицы
int i,j, rezult;// рабочие переменные
Char c;
printf("\nRazmer matricy n=");
scanf("%d", &n);
float a[n][n];// исходная матрица
float p[2][n];// массив собственных значений:
// первая строка - действительные части,
// вторая строка - мнимые части
// ввод исходной матрицы
printf("\n Vvesti matricu\n");
for (i=0; i<n; i++)
{
printf("\n stroka %d (%d chisel):\n", i+1, n);
for (j=0; j<n; j++)
scanf("%f", &a[i][j]);
}
printf("\n\n");
rezult=gessenberger(n, a, p);
if(rezult==0)// нормальное завершение
{
printf("\n Sobstv. znachenija");
printf("\n Dejstvit. chasti Mnimye chasti \n");
for (i=0; i<n; i++)
printf(" %12.6f %12.6f\n", p[0][i], p[1][i]);
printf("\n");
}
c=getch();
Return 0;
}
Результат работы программы:
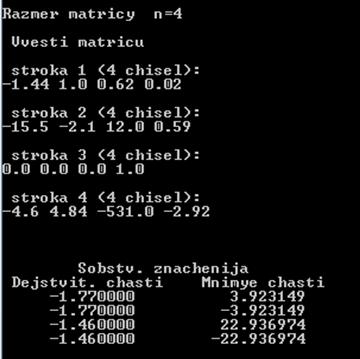
Таким образом,
p1,2 = -1.77 ± j 3.92315 p3,4 = -1.46 ± j 22.93697
Вычисление коэффициентов характеристического полинома
и обратной матрицы методом Леверрье-Фаддеева
В головной программе необходимо:
1. описать прототип функции:
void invers(int n, float a[n][n], float invert[n][n], float q[n+1]);
2. ввести значение переменной n – размер исходной матрицы,
3. описать массивы:
float a[n][n]; // исходная матрица
float invert[n][n]; // обратная ей матрица
float q[n+1]; // вектор коэффициентов ее характеристического
// полинома по возрастанию степеней
4. ввести исходную матрицу a[n][n],
5. обратиться к программе вычисления собственных значений:
Invers(n, a, invert, q);
6. вывести на экран терминала (в текстовый файл) обратную матрицу и вектор коэффициентов характеристического полинома исходной матрицы,
Пример: вычислить обратную матрицу и коэффициенты характеристического полинома для следующей матрицы ( n=3):
0.0 1.0 0.0
a[3][3]= 0.0 0.0 1.0
-2.0 -3.0 -3.0
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
void invers(int n, float a[n][n], float invert[n][n], float q[n+1]);
int main(int argc, char **argv)
{
int n;// размер исходной матрицы
int i,j;// рабочие переменные
Char c;
printf("\n n=");
scanf("%d", &n);
float a[n][n], invert[n][n], q[n+1];
// a[n][n] - исходная матрица
// invert[n][n] - обратная матрица;
// q[n+1] - коэффициенты характеристического полинома по
// убывающим степеням,
// причем коэффициент при старшей (n-ой степени)
// всегда равен единице
// ввод исходной матрицы построчно
printf("\n Vvesti matricu\n");
for (i=0; i<n; i++)
{
printf("\n stroka %d (%d chisel):\n", i+1, n);
for (j=0; j<n; j++)
scanf("%f", &a[i][j]);
}
printf("\n\n");
Invers(n, a, invert, q);
printf("\n Harakt. polinom:\n");
for (i=0; i<n+1; i++)
printf("%10.3f", q[i]);
printf("\n\n");
printf("\n Obratn. matriza:\n");
for (i=0; i<n; i++)
{
for (j=0; j<n; j++)
printf("%10.3f", invert[i][j]);
printf("\n");
}
printf("\n\n");
c=getch();
Return 0;
}
Результат работы программы:
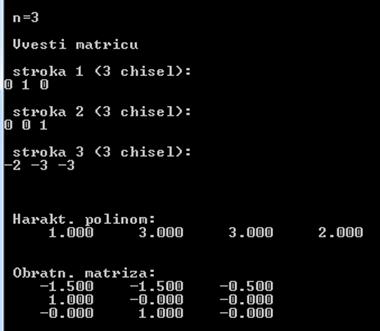
Таким образом, характеристический полином исходной матрицы имеет вид:
W(p) = p4 + 3p3 + 3p2 +2
Вычисление коэффициентов характеристического полинома матрицы методом Данилевского (приведение матрицы к форме Фробениуса)
В головной программе необходимо:
1. описать прототип функции:
int danilevski(int n, float a[n][n], float q[n+1]);
2. ввести значение переменной n – размер исходной матрицы,
3. описать массивы:
float a[n][n]; // исходная матрица
float q[n+1]; // вектор коэффициентов ее характеристического
// полинома по возрастанию степеней
4. ввести исходную матрицу a[n][n],
5. обратиться к программе вычисления собственных значений:
rezult=danilevski(n, a, q);
6. вывести на экран терминала (в текстовый файл) матрицу Фробениуса и вектор коэффициентов характеристического полинома
Пример: вычислить матрицу Фробениуса и коэффициенты характеристического полинома для следующей матрицы ( n=4):
-4.0 -3.0 1.0 1.0
a[4][4]= 2.0 0.0 4.0 -1.0
1.0 1.0 2.0 -2.0
1.0 1.0 -1.0 -1.0
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
int danilevski(int n, float a[n][n], float q[n+1]);
int main(int argc, char **argv)
{
int n;// размер исходного массива
int i,j, rezult;// рабочие переменные
Char c;
printf("\n n=");
scanf("%d", &n);
float a[n][n];// исходная матрица, после вычислений –
// матрица Фробениуса
float q[n+1];// вектор коэффициентов ее
// характеристического полинома
// по возрастающим степеням
// ввод исходной матрицы
printf("\n Vvesti matricu\n");
for (i=0; i<n; i++)
{
printf("\n stroka %d (%d chisel):\n", i+1, n);
for (j=0; j<n; j++)
scanf("%f", &a[i][j]);
}
printf("\n\n");
rezult=danilevski(n, a, q);
if (rezult==0)// все нормально
{
printf ("\nMatrica Frobeniusa:\n");
for (i=0; i<n; i++)
{
for (j=0; j<n; j++)
printf("%10.5f", a[i][j]);
printf("\n");
}
printf("\n\n");
printf("\n Koeff. harakterist. polinoma:\n");
for (i=0; i<n+1; i++)
printf("%12.6f", q[i]);
printf("\n\n");
}
c=getch();
Return 0;
}
Результат работы программы:
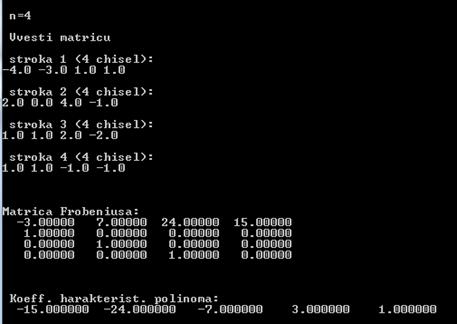
Таким образом, характеристический полином исходной матрицы имеет вид:
W(p) = p4 + 3p3 - 7p2 – 24p -15
Разложение действительной неособенной квадратной матрицы
на произведение двух треугольных (LU-разложение)
В головной программе необходимо:
1. описать прототип функции:
int LU(int n, float a[n][n]);
2. ввести значение переменной n – размер исходной матрицы,
3. описать массивы:
float a[n][n]; // исходная матрица, после вычислений -
// LU-матрица
7. ввести исходную матрицу a[n][n],
5. обратиться к программе вычислений:
rezult=LU(n, a);
6. вывести на экран терминала (в текстовый файл) LU-матрицу.
Пример: вычислить LU-матрицу для следующей исходной матрицы ( n=4):
-1.44 1.0 0.62 0.02
a[4][4]= -15.5 -2.1 12.0 0.59
0.0 0.0 0.0 1.0
-4.6 4.84 -531.0 -2.92
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
int LU(int n, float a[n][n]);
int main(int argc, char **argv)
{
int n;// размер исходного массива
int i,j, rezult;// рабочие переменные
Char c;
printf("\n n=");
scanf("%d", &n);
float a[n][n];// исходная матрица, после вычислений –
// LU-матрица
// ввод исходной матрицы
printf("\n Vvesti matricu\n");
for (i=0; i<n; i++)
{
printf("\n stroka %d (%d chisel):\n", i+1, n);
for (j=0; j<n; j++)
scanf("%f", &a[i][j]);
}
printf("\n\n");
rezult=LU(n, a);
if(rezult==0)// нормальное завершение
{
printf("\n LU-matrica:\n");
for (i=0; i<n; i++)
{
for(j=0; j<n; j++)
printf("%12.6f", a[i][j]);
printf("\n");
}
}
else printf("\n Reshenija net!\n");
printf("\n\n");
c=getch();
Return 0;
}
Результат работы программы:
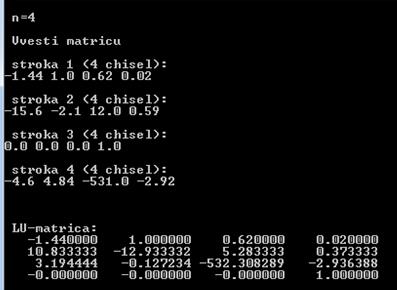
Таким образом,
1.0 0.0 0.0 0.0
L= 10.8333 1.0 0.0 0.0
3.1944 -0.1272 1.0 0.0
0.0 0.0 0.0 1.0
L-матрица – это нижняя треугольная матрица с единицами по главной диагонали.
-1.44 1.0 0.62 0.02
U= 0.0 -12.9333 5.2833 0.3733
0.0 0.0 -532.3083 -2.9364
0.0 0.0 0.0 1.0
U-матрица – это верхняя треугольная матрица.
Минимизация функции многих переменных
модифицированным методом Пауэлла
В головной программе необходимо:
1. описать прототип функции:
void minim_modificir_Powell(int n, float x[n], float eps, int *iter, float *minimum);
2. ввести значение переменной n – количество переменных,
3. описать вектор float x[n]-вектор начальных приближений переменных, после вычислений – вектор минимизирующих значений переменных,
4. ввести вектор x[n],
5. ввести порог минимизацииeps,
6. описать минимизируемую функцию в функции float function(float x[]),например:
float function(float x[])
{
Float f;
f=100.0*(x[1]-x[0]*x[0])*(x[1]-x[0]*x[0]) + (1.0-x[0])*(1.0-x[0]);
Return f;
}
7. обратиться к программе вычислений :
minim_modificir_Powell(n, x, eps, &iter, &minimum);
8. вывести на экран терминала (в текстовый файл) массив x[n],количество итераций iter, минимальное значение функции minimum.
Пример: найти минимум функции Розенброка
f(x1, x2) = 100(x2 – x12)2 + (1 – x1)2
при начальных приближениях x1=5.0, x2=10.0 и eps=1.0e-10.
Точное решение: fmin = 0.0 при x1=1.0, x2=1.0 .
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
void minim_modificir_Powell(int n, float x[n], float eps, int *iter, float *minimum);
int main(int argc, char **argv)
{
int n;// количество переменных
int i;// рабочая переменная для ввода исходных данных
Char c0;
printf("\nKol-vo peremenn. n= ");
scanf("%d", &n);
float x[n];// вектор начальных приближений переменных,
// по окончании вычислений- вектор
// минимизирующих значений переменных
float eps;// порог минимизации функции
int iter;// количество выполненных итераций
float minimum;// значение минимума функции
printf("\nVvedite vector nach. pribl.(%d znacheniy):\n", n);
for (i=0; i<n; i++)
scanf("%f", &x[i]);
printf("\nVvedite porog minimiz. funkcii:");
scanf("%e", &eps);
printf("\n");
printf("\nMinimiz. funkcii modific. metodom Pauella\n");
minim_modificir_Powell(n, x, eps, &iter, &minimum);
printf("\nMinimizir. znach. peremenn.:\n");
for (i=0; i<n; i++)
printf("%10.5f", x[i]);
printf("\n");
printf("\nMinim. znach. funkcii: %e\n", minimum);
printf("\nKol-vo iterac.: %d\n", iter);
c0=getch();
Return 0;
}
Описание минимизируемой функции:
float function(float x[])
{
Float f;
f=100.0*(x[1]-x[0]*x[0])*(x[1]-x[0]*x[0]) + (1.0-x[0])*(1.0-x[0]);
Return f;
}
Результат работы программы:
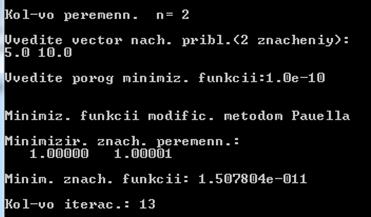
Таким образом, найденное минимальное значение функции fmin = 1,5078e-11
при x1 = 1,0 и x2 = 1,0 и 13 итерациях.
Минимизация функции многих переменных
методом Давидона-Флетчера-Пауэлла
В головной программе необходимо:
1. описать прототип функции:
void minim_Davidon_Fletcher_Powell(int n, float x[n], float eps, int *iter, float *minimum);
2. ввести значение переменной n – количество переменных,
3. описать вектор float x[n]-вектор начальных приближений переменных, после вычислений – вектор минимизирующих значений переменных,
4. ввести вектор x[n],
5. ввести порог минимизацииeps,
6. описать минимизируемую функцию в функции float function(float x[]),например:
float function(float x[])
{
Float f;
f=100.0*(x[1]-x[0]*x[0])*(x[1]-x[0]*x[0]) + (1.0-x[0])*(1.0-x[0]);
Return f;
}
7. обратиться к программе вычислений :
minim_Davidon_Fletcher_Powell(n, x, eps, &iter, &minimum);
8. вывести на экран терминала (в текстовый файл) массив x[n],количество итераций iter, минимальное значение функции minimum.
Пример: найти минимум функции Розенброка
f(x1, x2) = 100(x2 – x12)2 + (1 – x1)2
при начальных приближениях x1=5.0, x2=10.0 и eps=1.0e-10.
Точное решение: fmin = 0.0 при x1=1.0, x2=1.0 .
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
void minim_Davidon_Fletcher_Powell(int n, float x[n], float eps, int *iter, float *minimum);
int main(int argc, char **argv)
{
int n;// количество переменных
int i;// рабочая переменная для ввода исходных данных
Char c0;
printf("\nKol-vo peremenn. n= ");
scanf("%d", &n);
float x[n];// вектор начальных приближений переменных,
// по окончании вычислений-
// вектор минимизирующих значений переменных
float eps;// порог минимизации функции
int iter;// количество выполненных итераций
float minimum;// значение минимума функции
printf("\nVvedite vector nach. pribl.(%d znacheniy):\n", n);
for (i=0; i<n; i++)
scanf("%f", &x[i]);
printf("\nVvedite porog minimiz. funkcii:");
scanf("%e", &eps);
printf("\n");
printf("\nMinimiz. funkcii metodom Davidona-Fletchera-Pauella\n");
minim_Davidon_Fletcher_Powell(n, x, eps, &iter, &minimum);
printf("\nMinimizir. znach. peremenn.:\n");
for (i=0; i<n; i++)
printf("%10.5f", x[i]);
printf("\n");
printf("\nMinim. znach. funkcii: %e\n", minimum);
printf("\nKol-vo iterac.: %d\n", iter);
c0=getch();
Return 0;
}
Описание минимизируемой функции:
float function(float x[])
{
Float f;
f=100.0*(x[1]-x[0]*x[0])*(x[1]-x[0]*x[0]) + (1.0-x[0])*(1.0-x[0]);
Return f;
}
Результат работы программы:
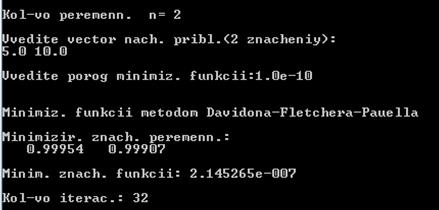
Таким образом, найденное минимальное значение функции fmin = 2,145265e-7
при x1 = 0,99954 и x2 = 0,99907 и 32 итерациях.
Решение системы обыкновенных дифференциальных уравнений
методом Рунге-Кутта четвертого порядка
с постоянным шагом интегрирования
В головной программе необходимо:
1. описать прототипы функций:
void Runge_Kutt_4(int n, float h, float t0, float t1, int s1, float x[n], float out[][n+1], int *k);
void graphics_diffur_koshi(int n, int k, int amplituda, char path[], float out[][n+1]);
2. ввести значение переменной n– порядок системы уравнений,
3. описать массив x[n] – вектор начальных условий (вектор решения),
4. описать массив out[k][n+1] – выходной массив:
количество строк – количество точек вывода k=(t1- t0)/(h*s1) + 1,
нулевой столбец – текущее время,
остальные столбцы – вектор решения (фазовые координаты),
5. ввести значение переменной h– шаг интегрирования,
6. ввести значения переменных t0, t1– начальное и конечное время интегрирования,
7. ввести значение переменной s1– количество шагов на один вывод решения,
8. в функции void pr_chasti(float x[], float p[])описать правые части системы дифференциальных уравнений в виде p[i]=p(x[j]) (нумерация элементов вектора правых частей p[n] и вектора решения x[n] начинается с нуля), например,
void pr_chasti(float x[], float p[])
{
p[0]=x[1];
p[1]=x[2];
p[2]=-2.0*x[0]-5.0*x[1]-2.5*x[2];
}
9. ввести массив x[n] – вектор начальных условий,
10. обратиться к программе вычислений :
Runge_Kutt_4(n, h, t0, t1, s1, x, out, &k);
Программа заполняет выходной массив out, который потом можно вывести на экран и использовать для вывода графиков.
Если необходимо вывести графики, то
- ввести значение переменой amplituda - амплитуда графиков функций в позициях (в текстовом файле),
- ввести строку path[30] - полный путь к текстовому файлу для вывода данных, например, d:/user/out.txt,
11. обратиться к программе вывода графиков :
