Пример. Идеальный газ двухатомных молекул
Между атомами молекулы имеется упругая связь, атомы совершают колебания. Такая система называется осциллятором. Молекулы независимы друг от друга. Полагаем, что поступательное, вращательное и колебательное движения молекулы происходят независимо, и между ними нет обмена энергией. Для колебательного движения молекулы найдем фазовую траекторию микросостояния и проверим выполнение теоремы Лиувилля.
1.Линейное колебание молекулы происходит с постоянной частотой ω и постоянной энергией E. Гамильтониан приравниваем полной энергии
.
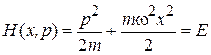В фазовом пространстве (x,p) микросостояние с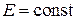 
движется по гиперповерхности с постоянной энергией. Это дает уравнение фазовой траектории микросостояния
,
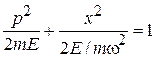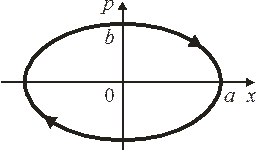
являющееся уравнением эллипса
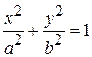
с полуосями
, 
,
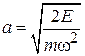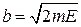показанными на рисунке. Разные микросостояния отличаются друг от друга начальной фазой.
2.Находим число микросостояний, используя (2.2а):
.
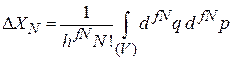Для рассматриваемого случая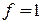 
, 
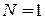и интеграл равен площади эллипса
,
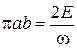тогда число микросостояний
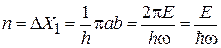, (П.2.4)
где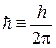 
. Поскольку n – целое число, то энергия осциллятора квантуется
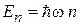, (П.2.4а)
где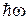 
– квант энергии. Число микросостояний равно числу квантов энергии осциллятора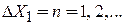 
На рисунке показан спектр энергиигармонического осциллятора. Горизонтальная линия – уровень энергии показывает возможное состояние осциллятора. Величина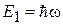 
равна энергии одного кванта, или интервалу эквидистантного спектра. На уровне 
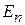осциллятор имеет n квантов энергии.
3.Для получения якобиана
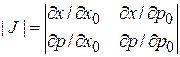
найдем функции
, 
,
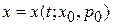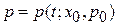где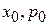 
– начальная координата и начальный импульс при 
.
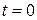В уравнения Гамильтона (2.1)
, 
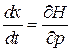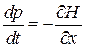
подставляем гамильтониан осциллятора
.
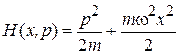Получаем
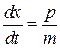– связь скорости с импульсом,
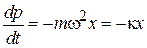– 2-й закон Ньютона 
,
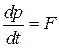где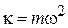 
– коэффициент жесткости упругой силы F;
.
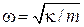Для решения системы двух уравнений дифференцируем первое уравнение
,
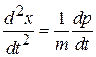подставляем второе и получаем уравнение гармонических колебаний
.
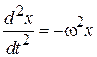Общее решение
,
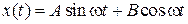тогда
.
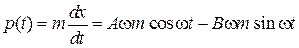Для нахождения параметров A и B накладываем начальные условия. При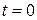
,
,
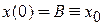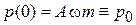получаем
, 
.
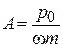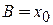В результате закон изменения координат микросостояния с течением времени
,
.
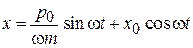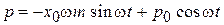Следовательно, микросостояния перемещаются по эллипсу по часовой стрелке с круговой частотой ω.
4.Вычисляем якобиан
.
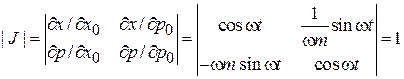Теорема Лиувилля выполняется.