Бросают игральных костей. Найти метематическое ожидание числа таких бросаний, в каждом из которых выпадет ровно шестерок, если общее число бросаний равно . 5 страница

Решение:

Обозначим через A событие – извлечена деталь отличного качества. Возможно три варианта гипотезы: 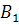– извлечена деталь отличного качества, изготовленная заводе №1; 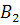– извлечена деталь отличного качества, изготовленная заводе №2; 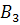– извлечена деталь отличного качества, изготовленная заводе №3. По условию 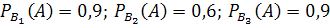. Найдём вероятности того, что извлечённая деталь изготовлена на заводе №1, №2, №3.

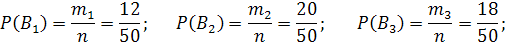
где 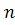- общее число изготовленных на 3-х заводах деталей, 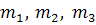– количество деталей изготовленных, соответственно, на заводах №1, 2, 3.

Искомая вероятность вероятность того, что извлеченная наудачу деталь окажется отличного качества находится по формуле полной вероятности:

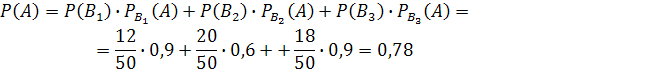
№94 В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.

Решение:

Обозначим через событие – извлечён белый шар. Возможны следующие гипотезы:

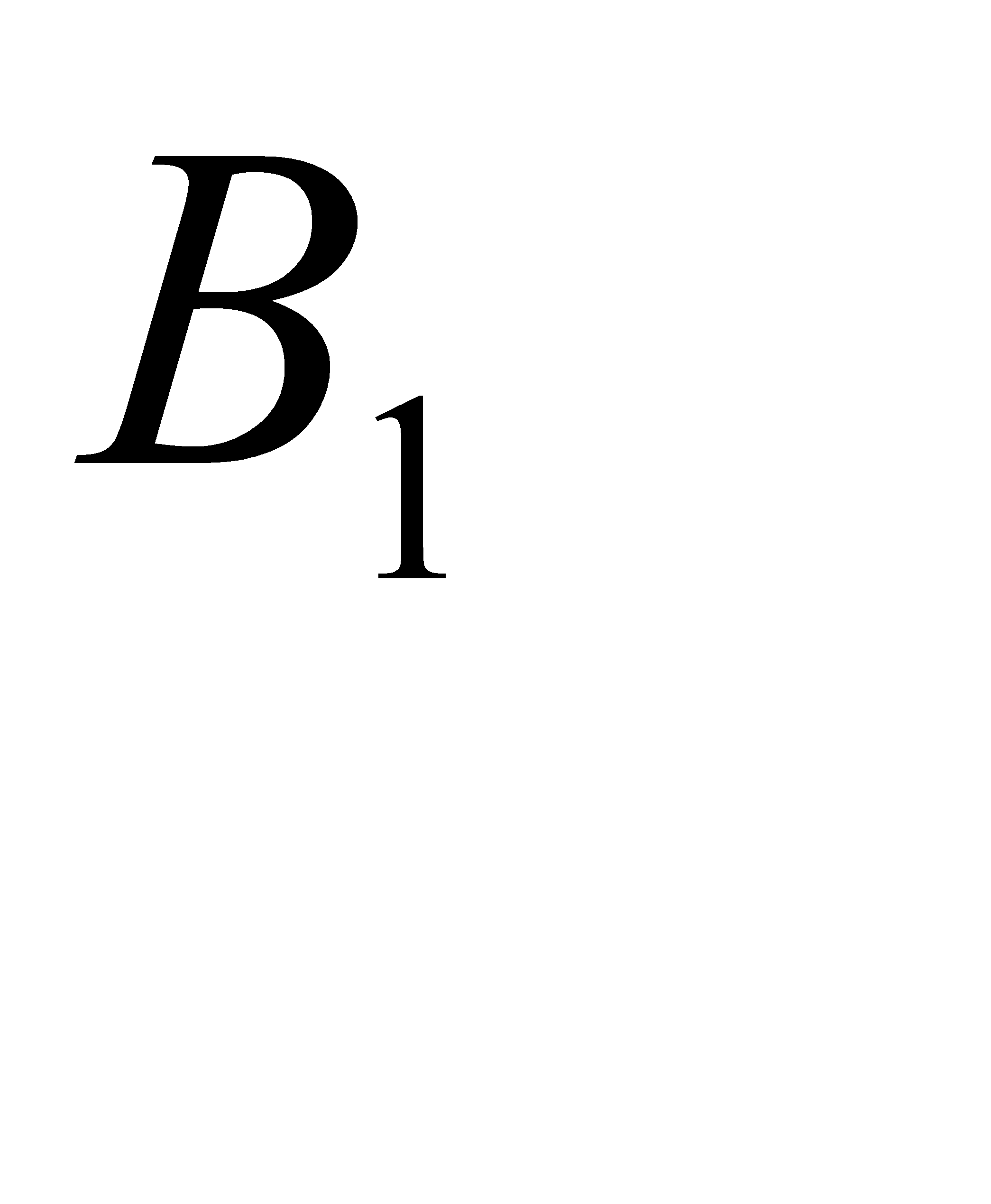- белый шар взят из первой урны, 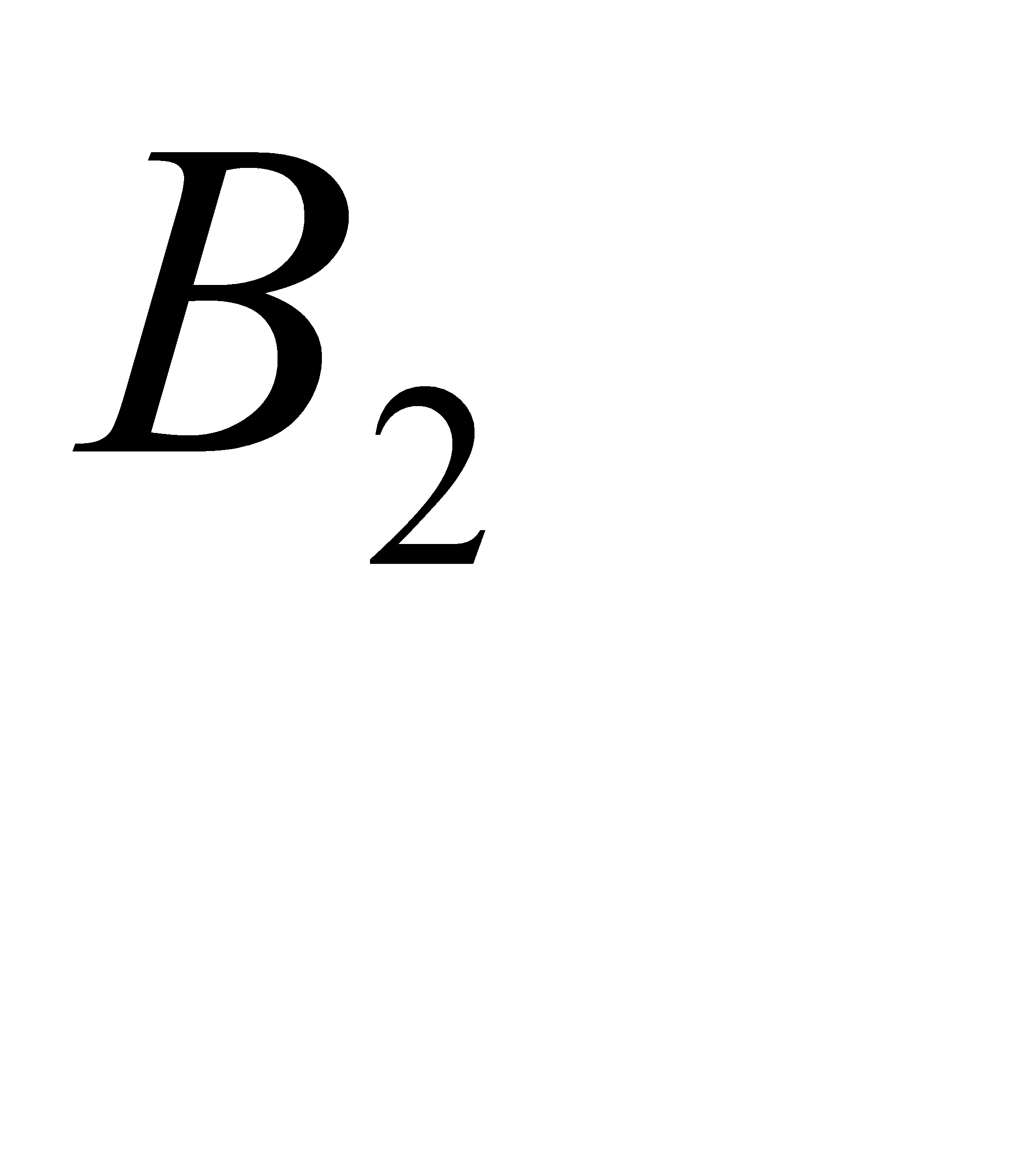- белый шар взят из второй урны.

Поскольку всего имеется две гипотезы, причём по условию они равновероятны, и сумма вероятностей гипотез равна единице(т.к. они образуют полную группу событий), то вероятность каждой из гипотез равна , т.е. .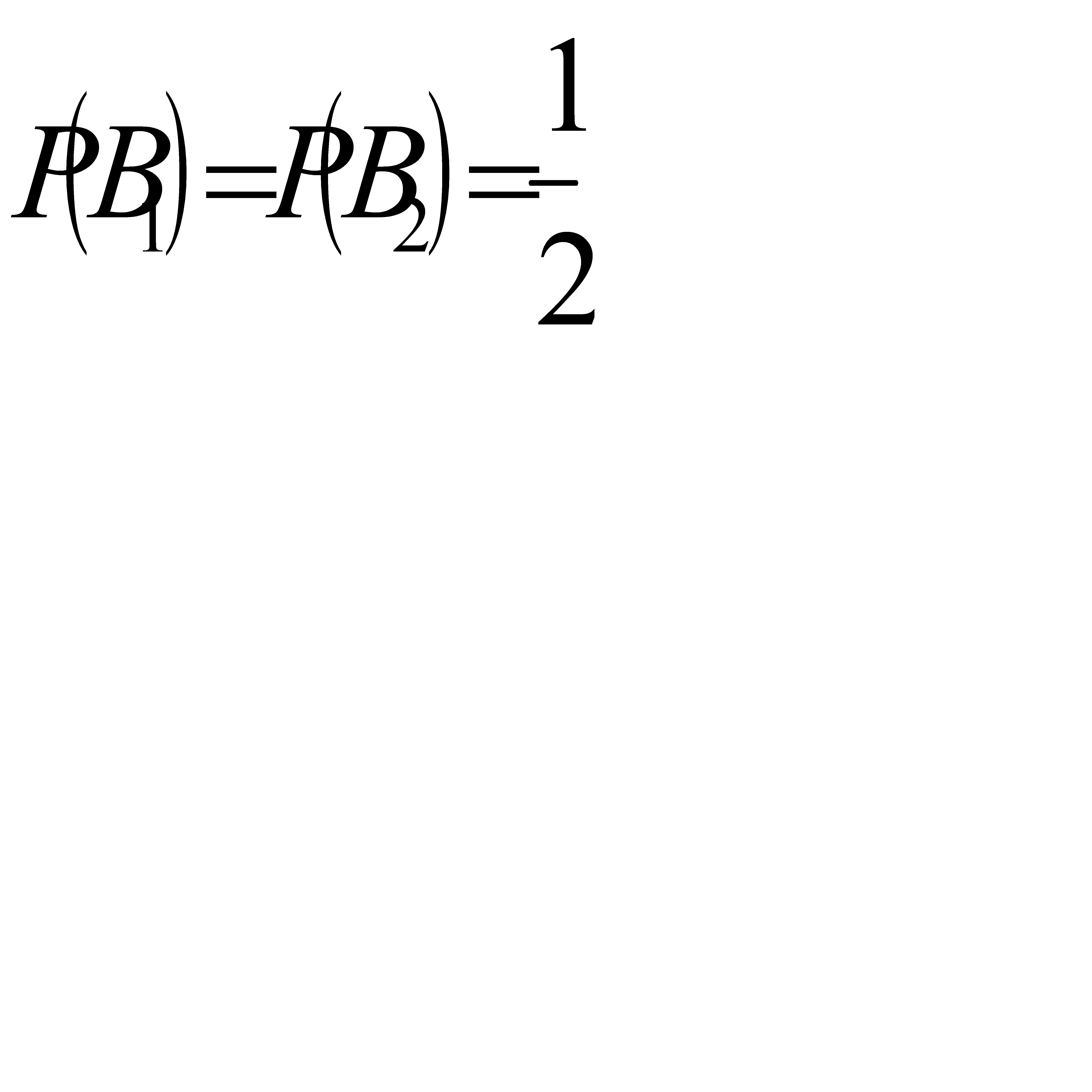

Условная вероятность того, что белый шар будет извлечён из первой урны равна: =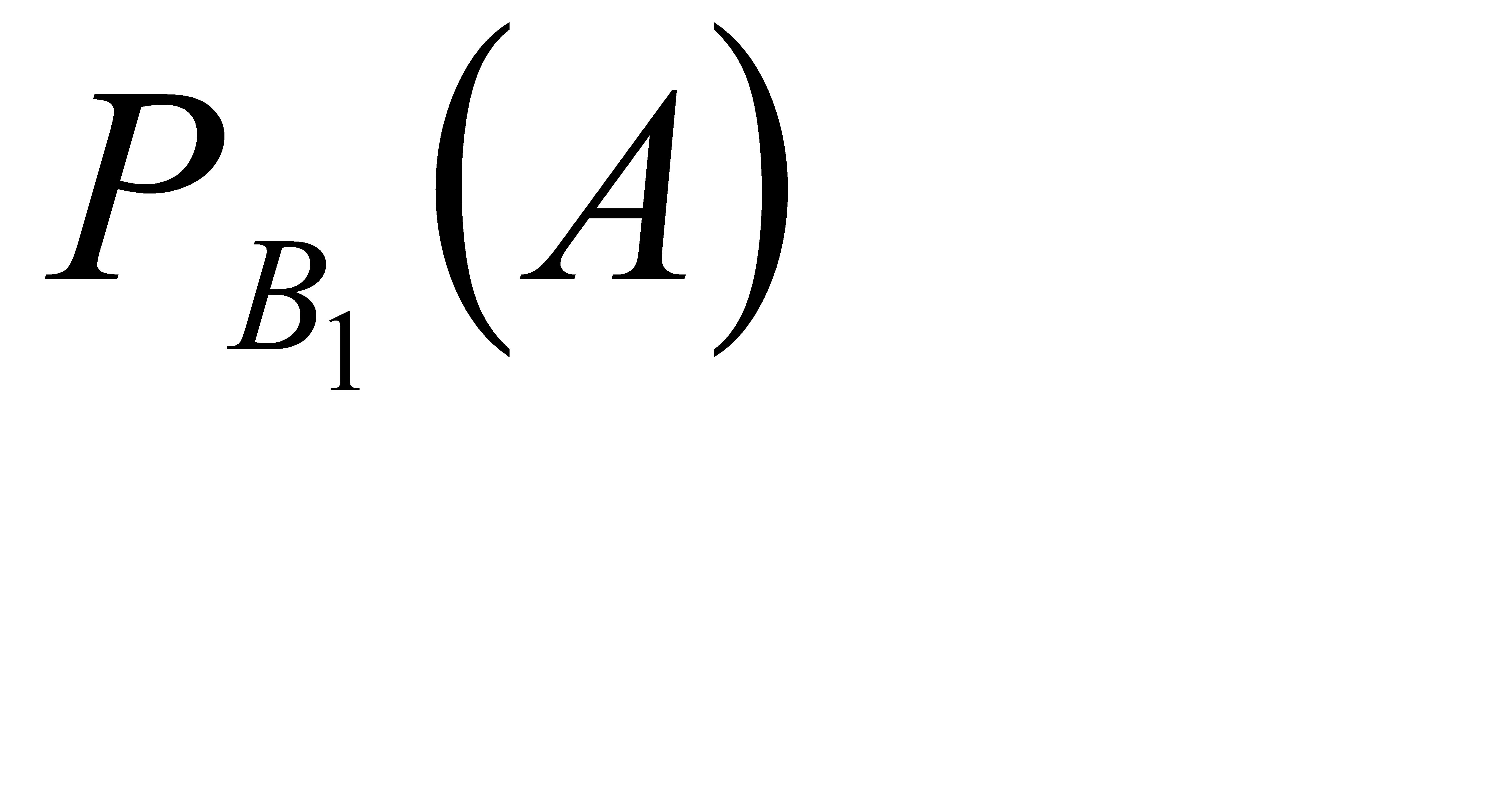

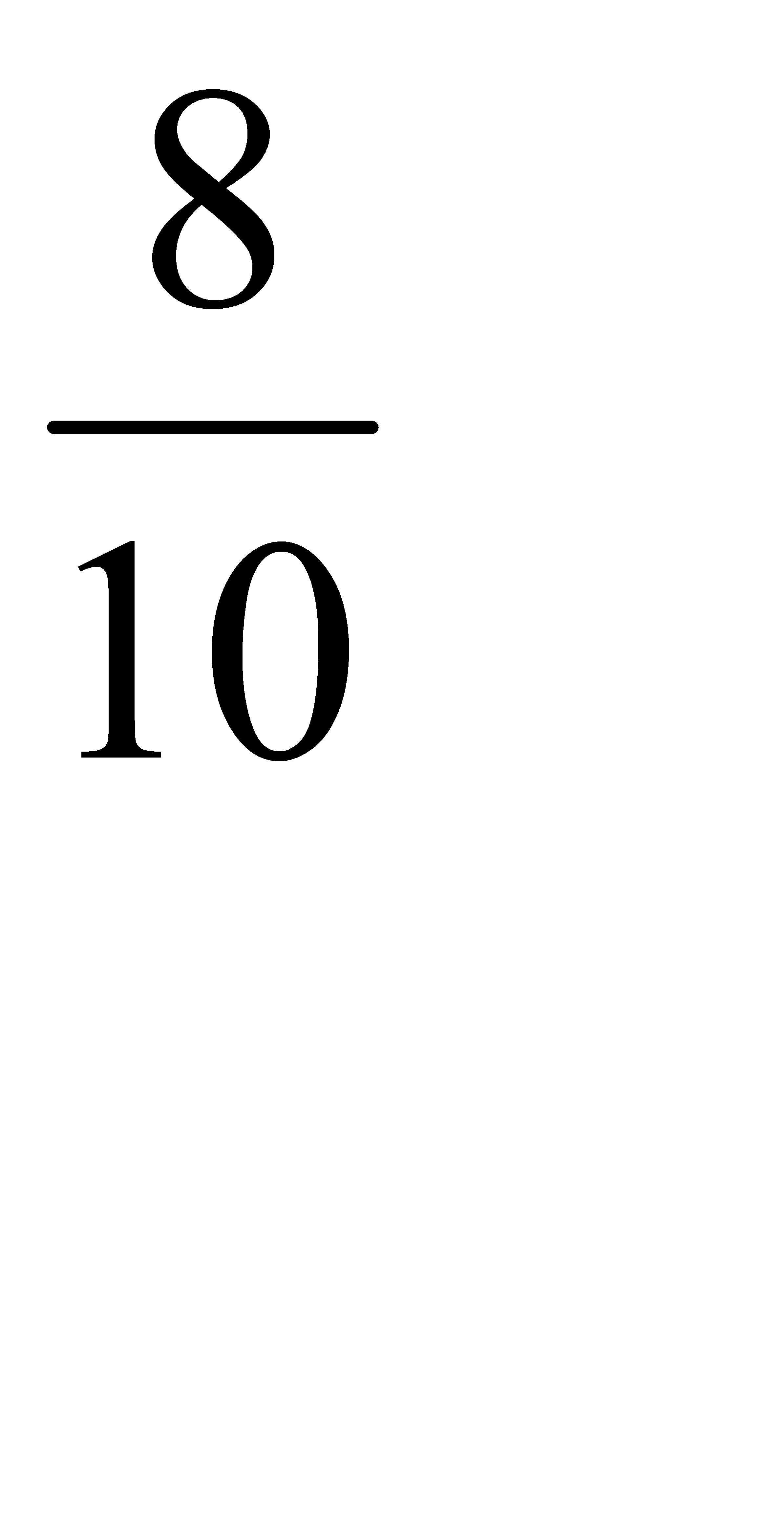
Условная вероятность того, что белый шар будет извлечён из второй урны равна: =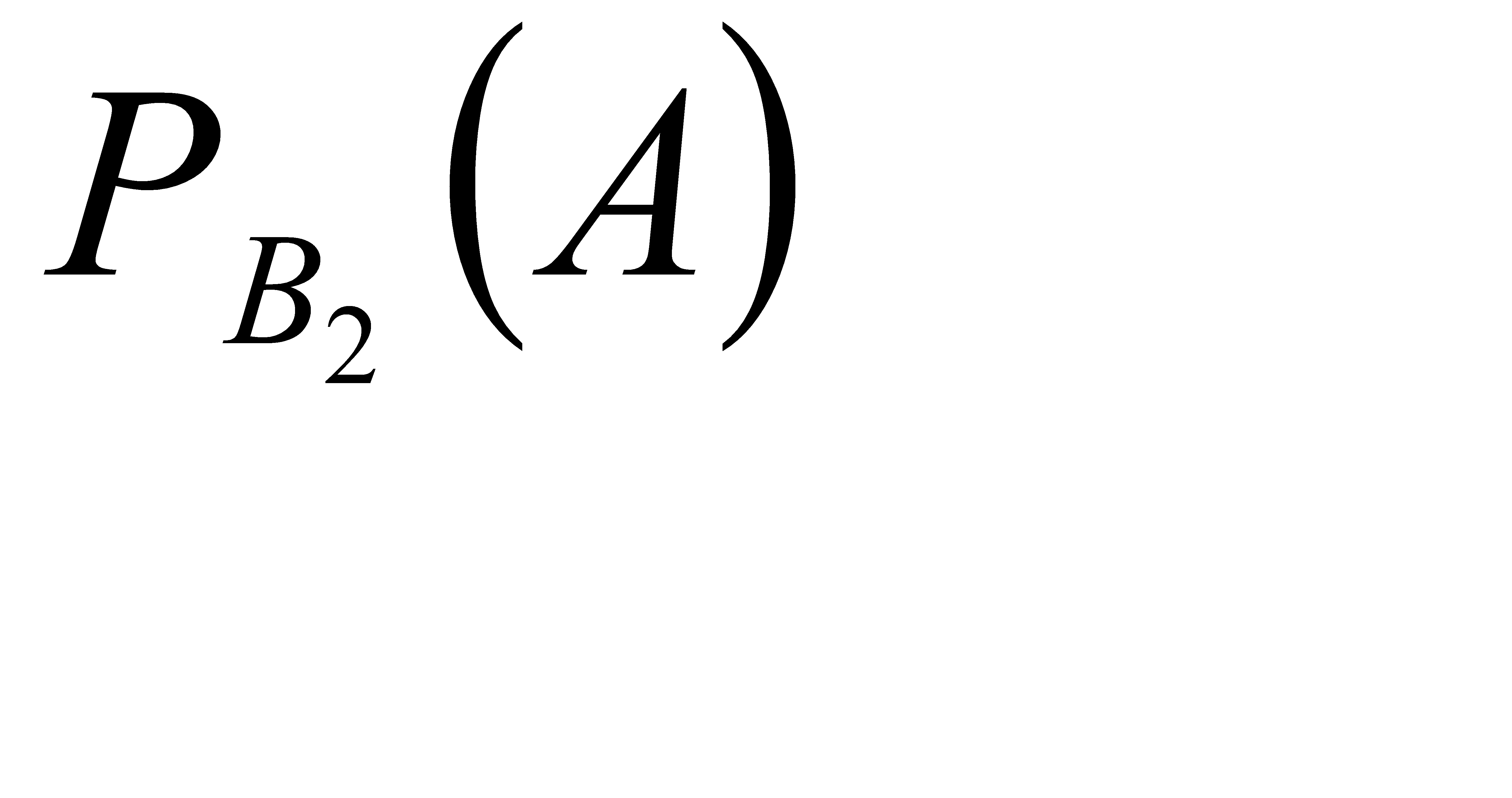

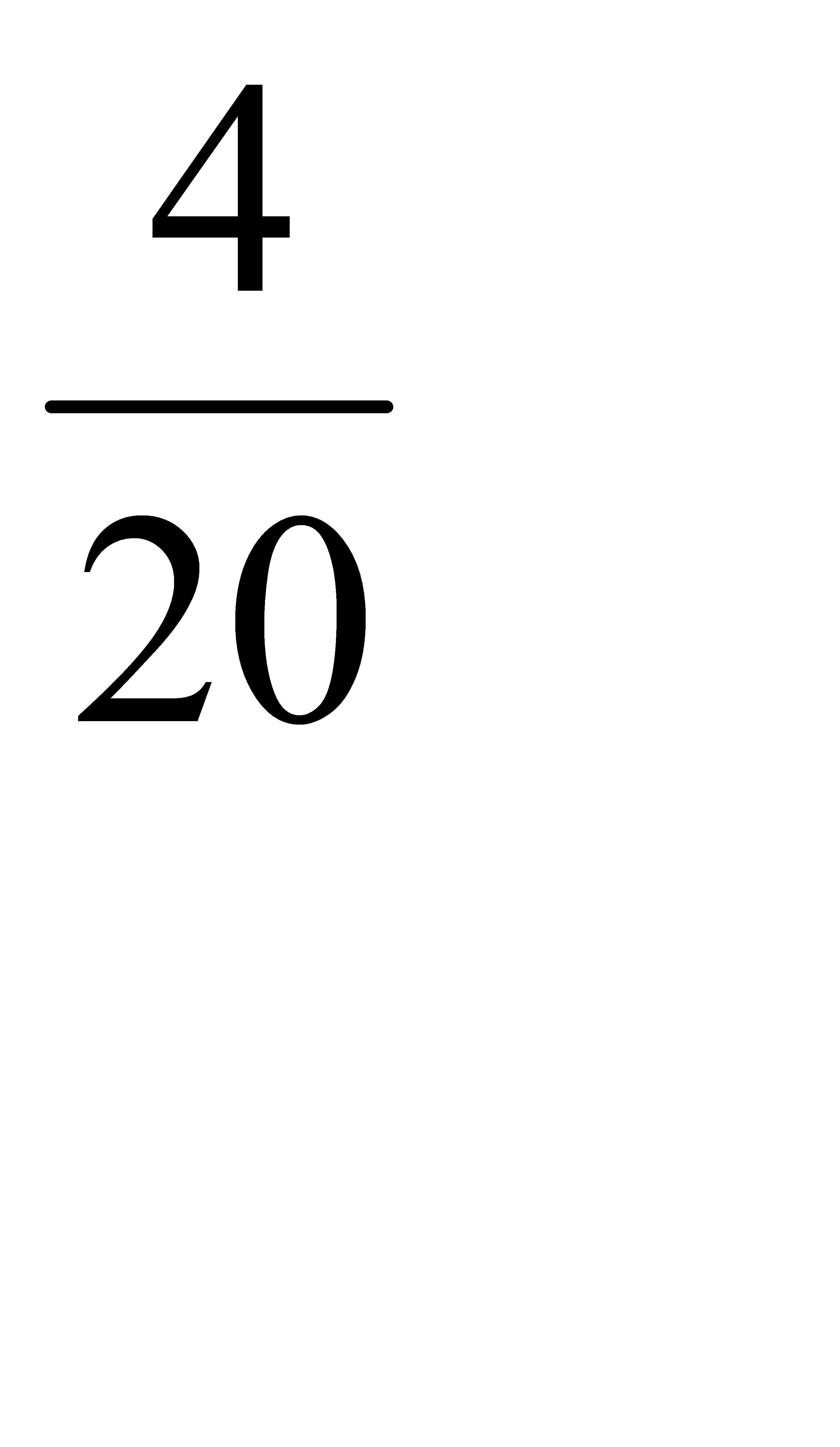
По формуле полной вероятности находим:

№ 95 В каждой из трех урн содержится 6 черных 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым.

Решение.

A1 – вероятность того, что из первой урны извлечен белый шар.

A2 – вероятность того, что из первой урны извлечен черный шар.

P(A1)=4/10 P(A2)=6/10

B1 – вероятность того, что из второй урны извлечен белый шар, после того как из первой урны переложили во вторую урну белый шар.

B2 – вероятность того, что из второй урны извлечен белый шар, после того как из первой урны переложили во вторую урну черный шар.

P(B1)=5/11 P(B2)=4/11

C1 – вероятность того, что из второй корзины будет извлечен белый шар.

C2 – вероятность того, что из второй корзины будет извлечен черный шар.

P(C1)=P(A1)*P(B1)+P(A2)*P(B2) P(C1)=4/10*5/11+6/10*4/11=2/5

P(C2)=1-P(C1) P(C2)=1-2/5=3/5

D1 – вероятность того, что из третьей урны извлечен белый шар, после того как из второй урны переложили в втретью урну белый шар.

D2 – вероятность того, что из третьей урны извлечен белый шар, после того как из второй урны переложили в втретью урну черный шар.

P(D1)=5/11 P(D2)=4/11

E – вероятность того, что из третьей урны будет извлечен белый шар.

P(E)= P(D1)*P(C1)+P(D2)*P(C2) P(E)=5/11*2/5+4/11*3/5=2/5

Ответ: 2/5.

№ 96 Вероятности того, что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.

Решение:

Пусть А – событие того, что сбой будет обнаружен, тогда из формулы полной вероятности следует, что:

P(A)= PB1PB1A+PB2PB2A+PB3PB3A= 0,3*0,8+0,2*0,9+0,5*0,9=0,87.

Ответ: 0,87.

№ 97 Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.

Решение:

Обозначим через А событие – деталь отличного качества

Можно сделать два предположения

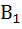-деталь произведена первым автоматом (так как производительность первого автомата вдвое больше второго автомата, то Р( 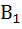)=2/3)

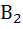-деталь произведена вторым автоматом (Р( 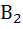)=1/3)

Условная вероятность, что она будет отличного качества, если она произведена первым автоматом 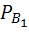(A)=0,6

Условная вероятность, что она будет отличного качества, если она произведена первым автоматом 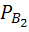(A)=0,84

Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна

P(A)=Р( 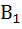)* 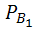(A)+ Р( 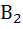)* 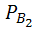(A)=2/3*0.6+1/3*0.84=0.68

Вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Бейеса равна

( )= = =

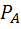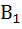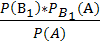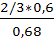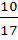
Ответ: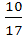

№ 98 В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?

Решение

Обозначим событие А – стрелок поразил мишень и гипотезы: B1 – стрелок выбрал винтовку с оптическим прицелом, B2 – без оптического прицела. Тогда 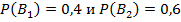. Условные вероятности попадания из винтовки с оптическим прицелом и без: 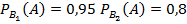. Вычислим вероятность попадания из наудачу взятой винтовки: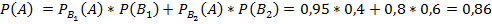

Теперь, воспользовавшись формулой Бейеса, получим ответ:

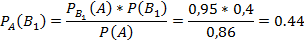
Ответ: Стрелок вероятнее всего стрелял из винтовки без оптического прицела.

№ 99 Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.

Решение:

Обозначим через А событие—подъезд автомобиля к заправке. Можно сделать два предположения: 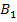—проехал грузовой автомобиль, причем 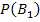=3/5; 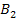— проехал легковой автомобиль, причем 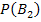= 2/5.

Условная вероятность, что проезжающий грузовой автомобиль подъедет на заправку: 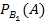= 0,1 . Для легкового: 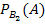= 0,2.

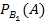
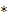
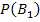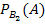
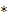
Вероятность того, что проезжающий автомобиль подъедет на заправку, по формуле полной вероятности равна Р(А) = + 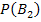= 3/5 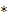0,1 + 2/5 0,2 = 0,14

Искомая вероятность того, что подъехавший к заправке автомобиль будет грузовым, по формуле Бейеса равна 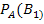= = 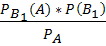= 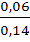3/7

Ответ: 3/7.

№ 100 Две перфораторщицы набили на разных перфораторах по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй перфораторщицы эта вероятность равна 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. (Предполагается, что оба перфоратора были исправны.)

Решение.

Обозначим через событие А – ошибку перфораторщицы. Тогда, 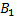– ошибка сделана первой перфораторщицей, 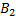- ошибка сделана второй перфораторщицей. Причем P( 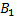)=0,5 и P( 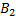)=0,5, т.к. обе работали одинаково.

Условная вероятность того, что первая перфораторщица допустит ошибку, равна 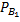(A)=0,05;

Условная вероятность того, что вторая перфораторщица допустит ошибку, равна 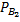(A)=0,1.

Вероятность того, что наудачу взятая перфокарта, окажется с ошибкой равна, по формуле полной вероятности равна:

P(A)= P( 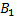)* 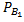(A)+ P( 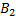)* 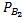(A)=0,5*0,05+0,5*0,1= .

Искомая вероятность того, что взятая перфокарта произведена первой перфораторщицей, по формуле Бейеса равна:

= = =

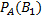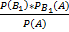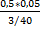№ 101 В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30%—с заболеванием L, 20%—с заболеванием М. Вероятность

полного излечения болезни К равна 0,7; для болезней L и М эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан

здоровым. Найти вероятность того, что этот больной страдал заболеванием К.

Решение

Больные поступают в больницу в разном процентном соотношении. Р(k)= 0.7, P(L)=0.3,P(M)= 0.2, где K,L,M – заболевания, а Р(Х)- вероятность поступления с данным заболеванием.Тогда Pk(A)=0.7, Pl(A)=0.8 ,Pm(A)=0.9 это вероятность полного излечения от данного заболевания. Чтобы найти вероятность что Больной, поступивший в больницу, был выписан здоровым надо найти :

P(A)= Pk(a)*P(k) + Pl(a)*P(l) + Pm(a)*P(m) = 0.7*0.5 + 0.8*0.3 + 0.9*0.2 = 0.77

А вероятность что больной страдал именно заболеванием К равно:

Pa(K) = (Pk(a)*P(k))/P(A)= (0.5*0.7)/0.77 = 5/11

№102 Изделие проверяется на стандартность одним из двух товароведов . Вероятность того, что изделие попадет к первому товароведу , равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом , равно 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того , что это изделие проверил второй товаровед.

Решение:

Обозначим через А – изделие признана стандартной. 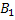- вероятность того, что изделие попало к первому товароведу. 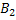- ко второму. P( 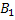) = 0,55 , P( 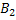) = 0,45.

Условная вероятность того что изделие будет признано стандартным первым товароведом равна 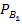(A) = 0,9, вторым - 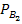(A) = 0,98.

Вероятность того, что изделие будет признано стандартным по формуле полной вероятности равна

P(A)= P( 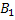) 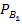(A) + P( 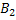) 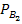(A) = 0,55 * 0,9 + 0,45 * 0,98 = 0,936

Искомая вероятность того, что изделие проверил второй товаровед, по формуле Бейеса равна

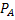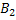( )= P( 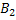) * 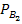(A) / P(A)= 0,45*0,98 / 0,936 = 0,47.

№ 103 Событие А может появится при условии появления одного из несовместимых событий В1, В2,…, Вn, образующих полную группу событий. После появления события А были переоценены вероятности гипотез, то есть были найдены условные вероятности РА(Вi) (i=1,2,…,n). Доказать, что сумма РА(Вi) (i=1,2,…,n) равна 1.

Решение:

По формуле Бейеса:

i=1n∑РА(Вi)= i=1n∑Р(Вi)* РВi(А)/Р(А)=Р(А)/Р(А)=1

Что и требовалось доказать.

№ 104 Событие 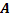может появиться при условии появления одного из несовместных событий (гипотез) 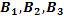, образующих полную группу событий. После появления события 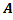были переоценены вероятности этих гипотез, т.е. были найдены условные вероятности этих гипотез, причем оказалось, что 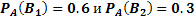. Чему равна условная вероятность 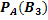гипотезы ?

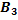Решение:

Так как события 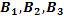образуют полную группу, и 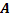появится при условии появления лишь одного из них, то верно 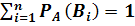. Так как имеем 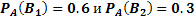, то: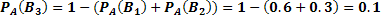

№ 105 Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 15, 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии.

Решение:

Обозначим через А событие – в каждом из двух испытаний была извлечена стандартная деталь. Можно предположить, что B1 – детали извлекались из первой партии; B2 – детали извлекались из второй партии; В3 – детали извлекались из третей партии.

Детали извлекались на удачу, поэтому вероятности предположений одинаковы:

P(B1) = P(B2) = P(B3) =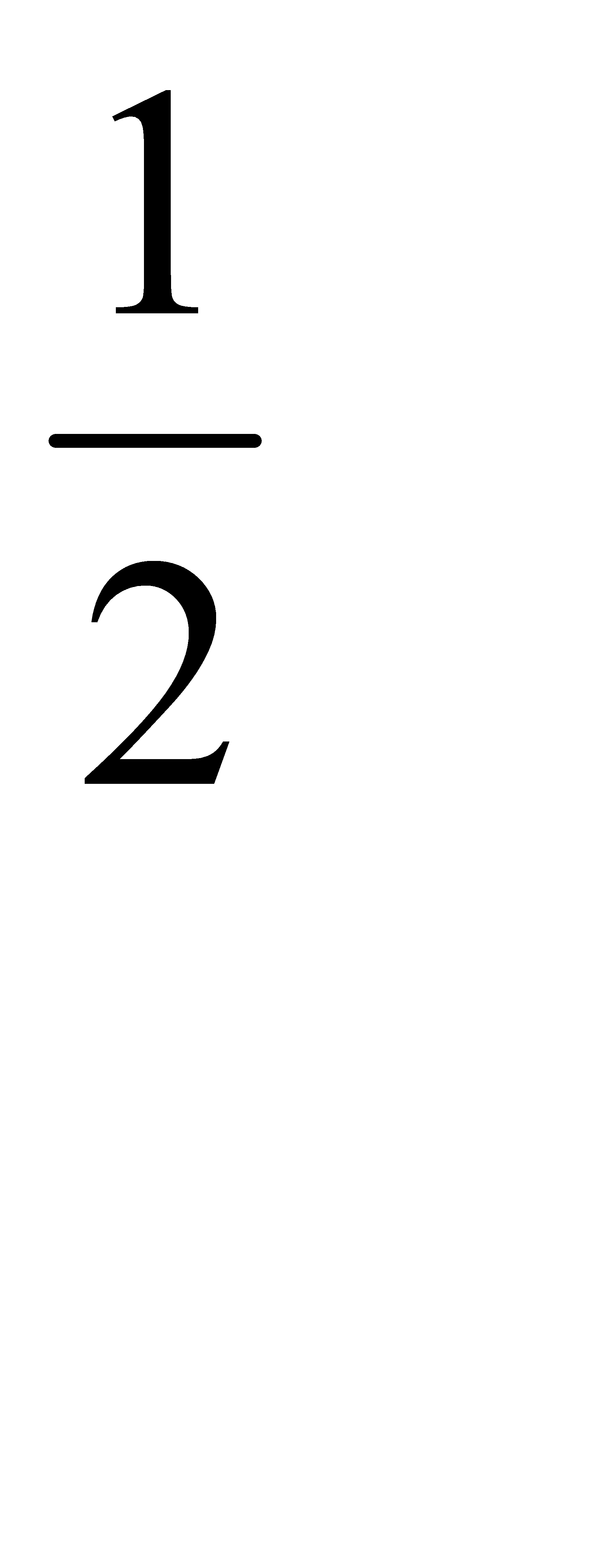

Вероятность того, что из первой партии будут последовательно извлечены две стандартные детали; поэтому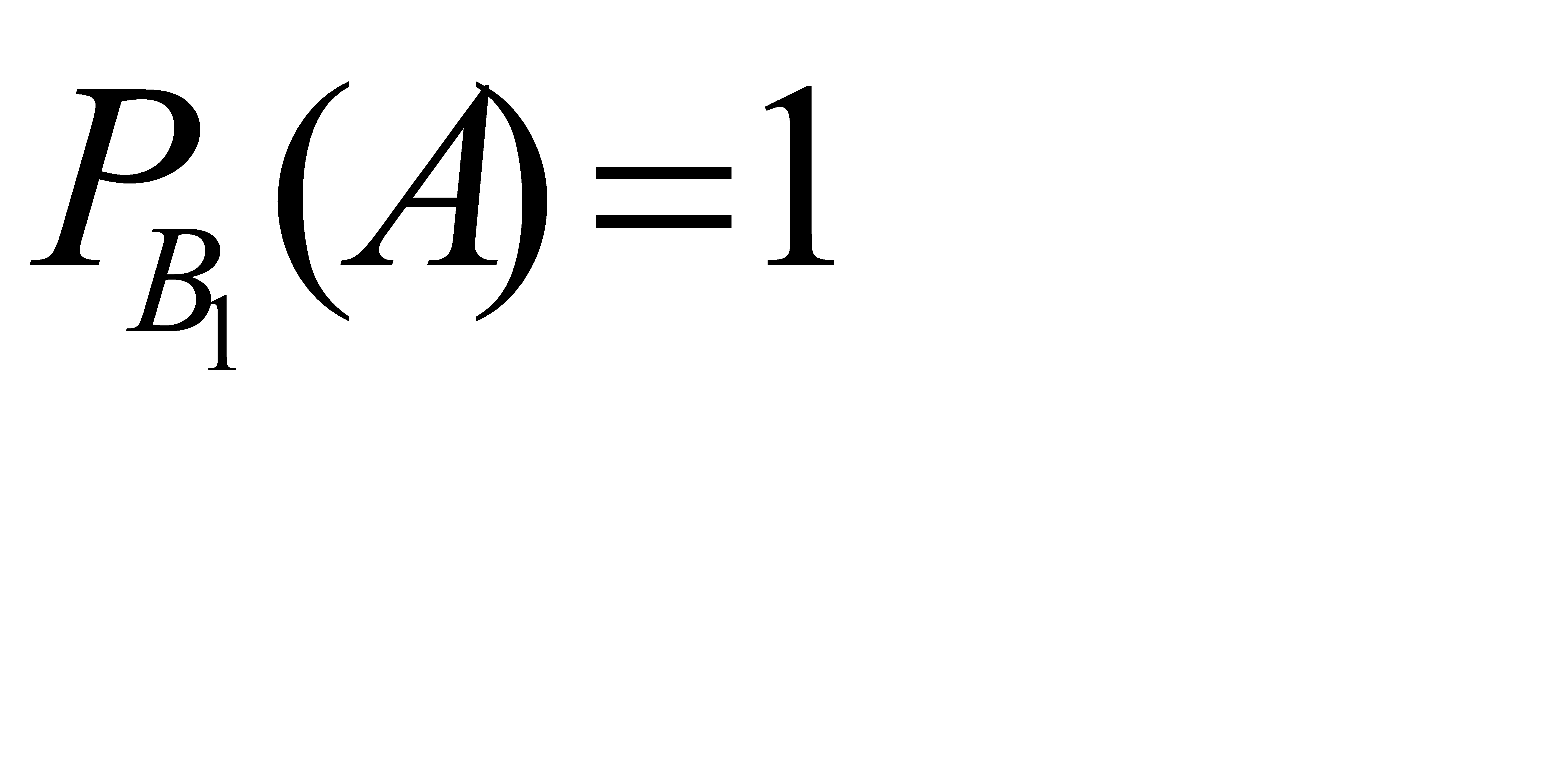

Условная вероятность 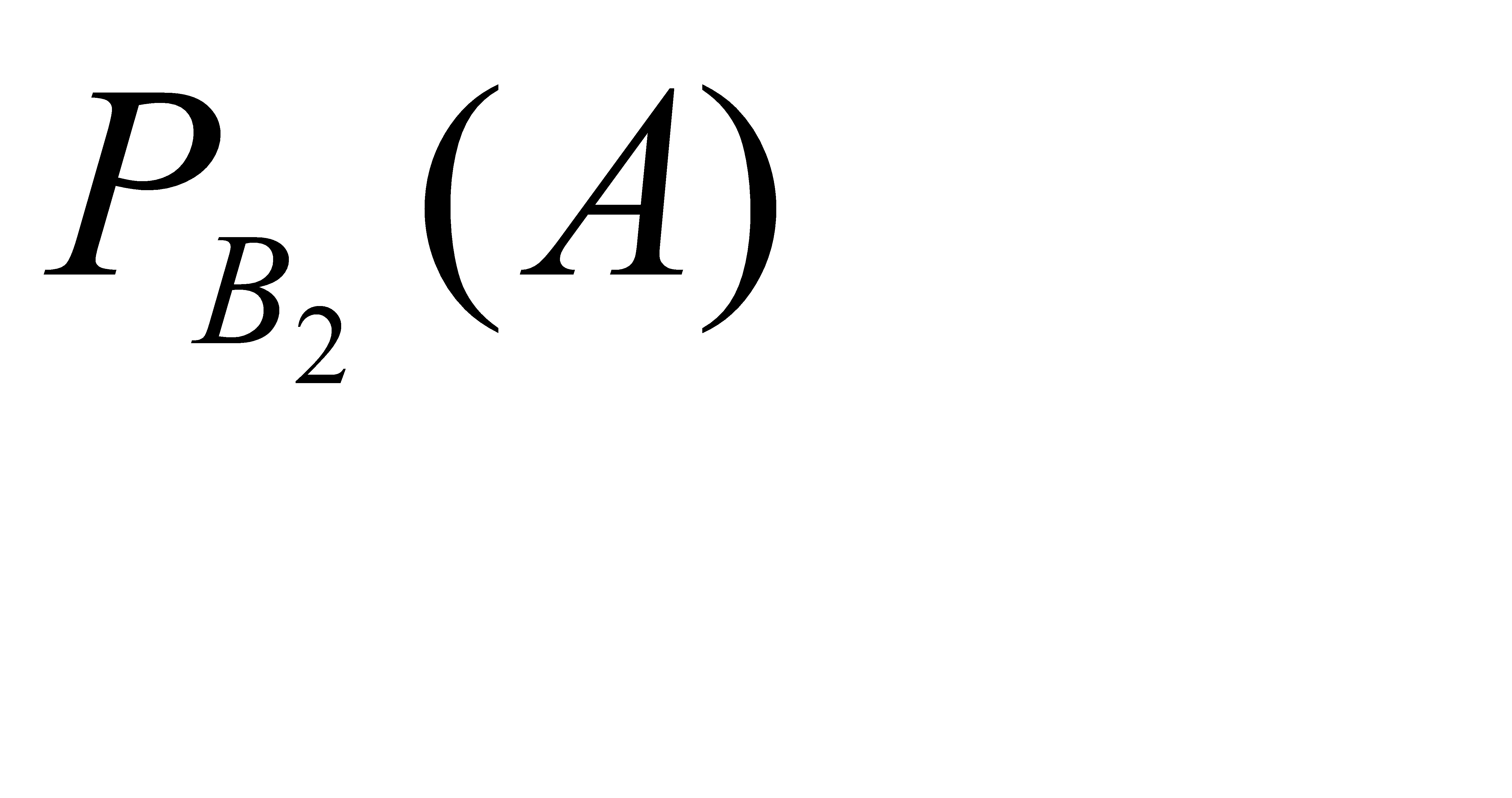т.е вероятность того, что из второй партии будут извлечены две стандартные детали: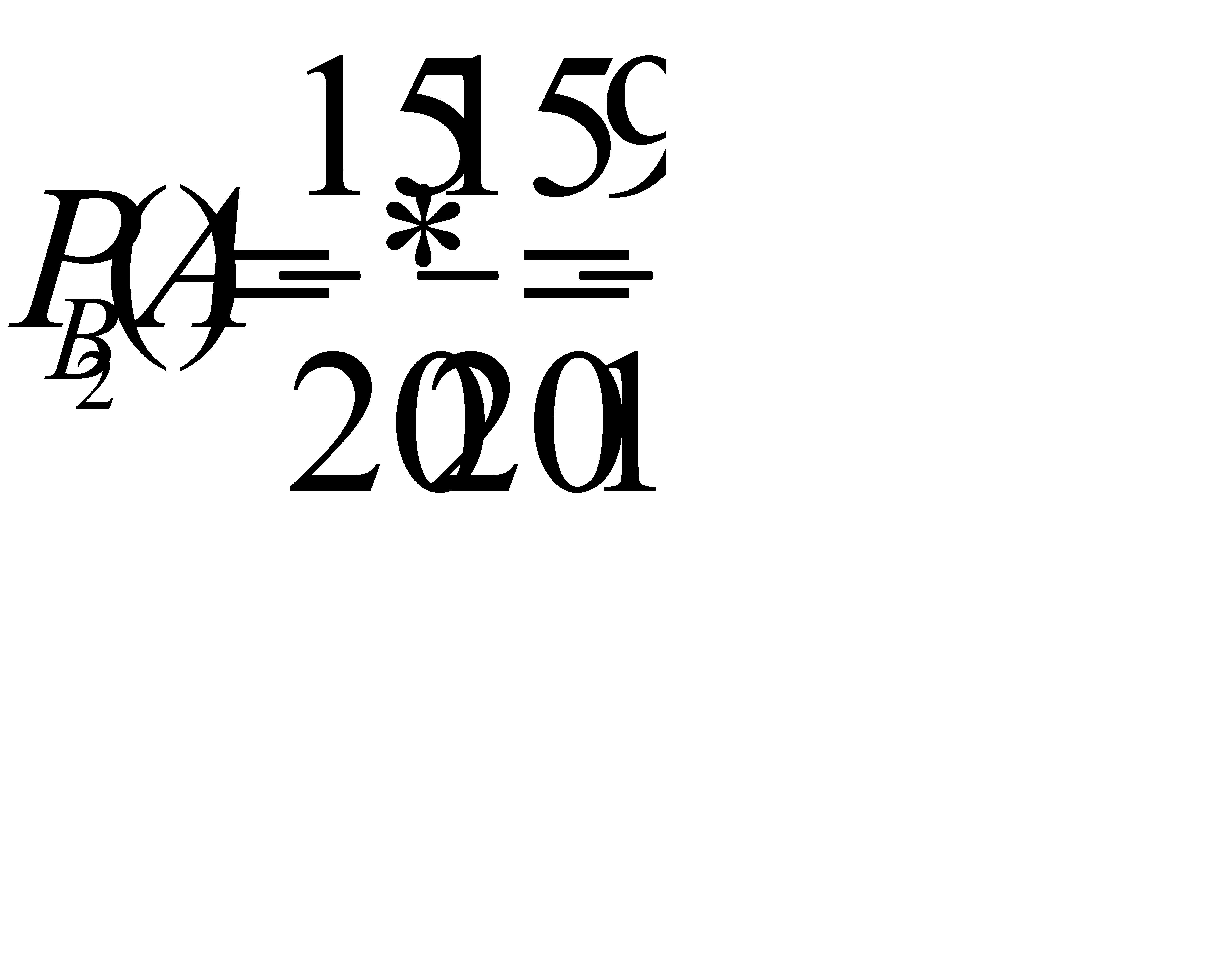

Найдем условную вероятность 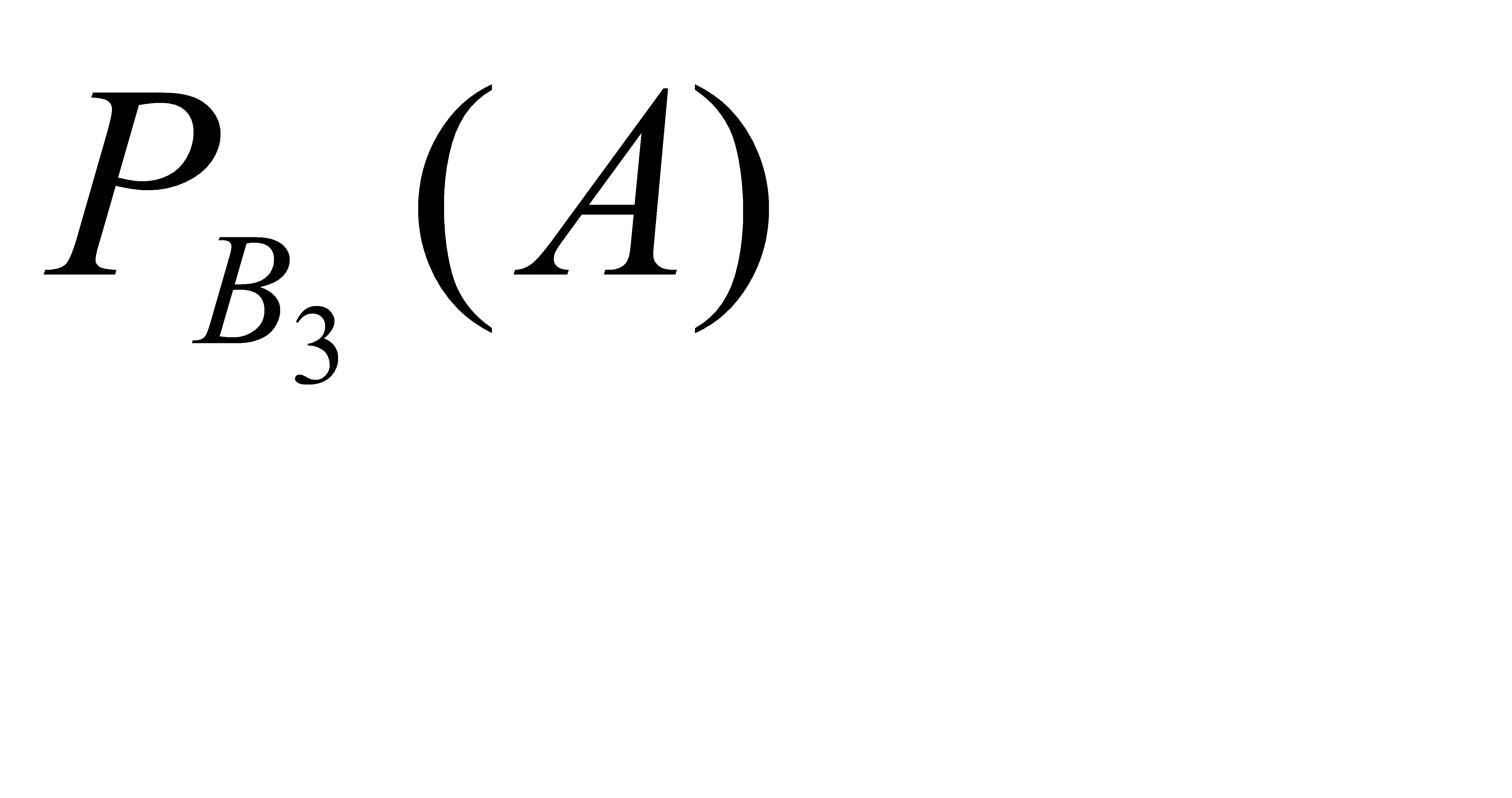т.е вероятность того, что из третей партии будут последовательно извлечены две стандартные детали: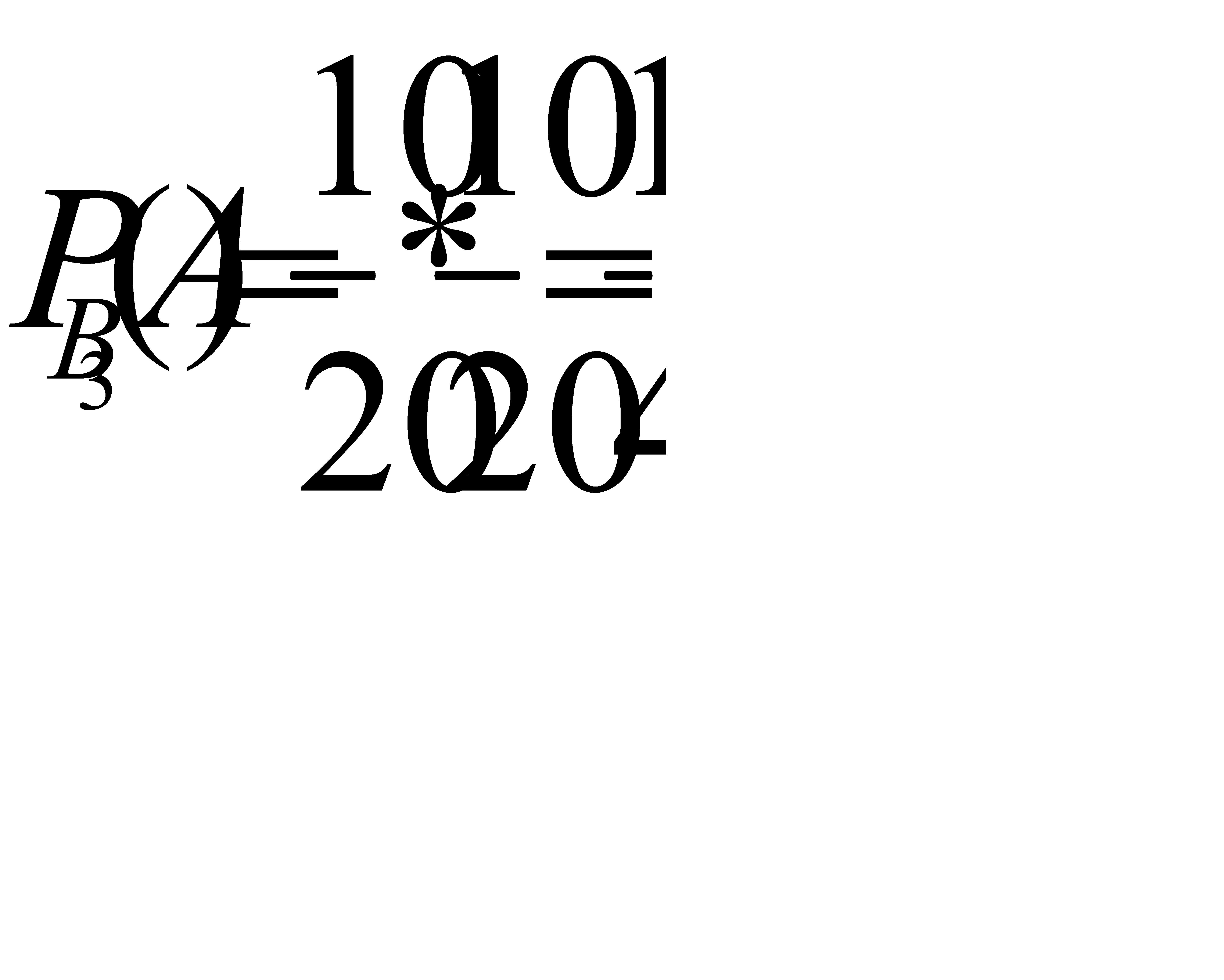

Искомая вероятность того, что обе извлеченные детали стандартные взяты из третей партии, по формуле Бейеса равна

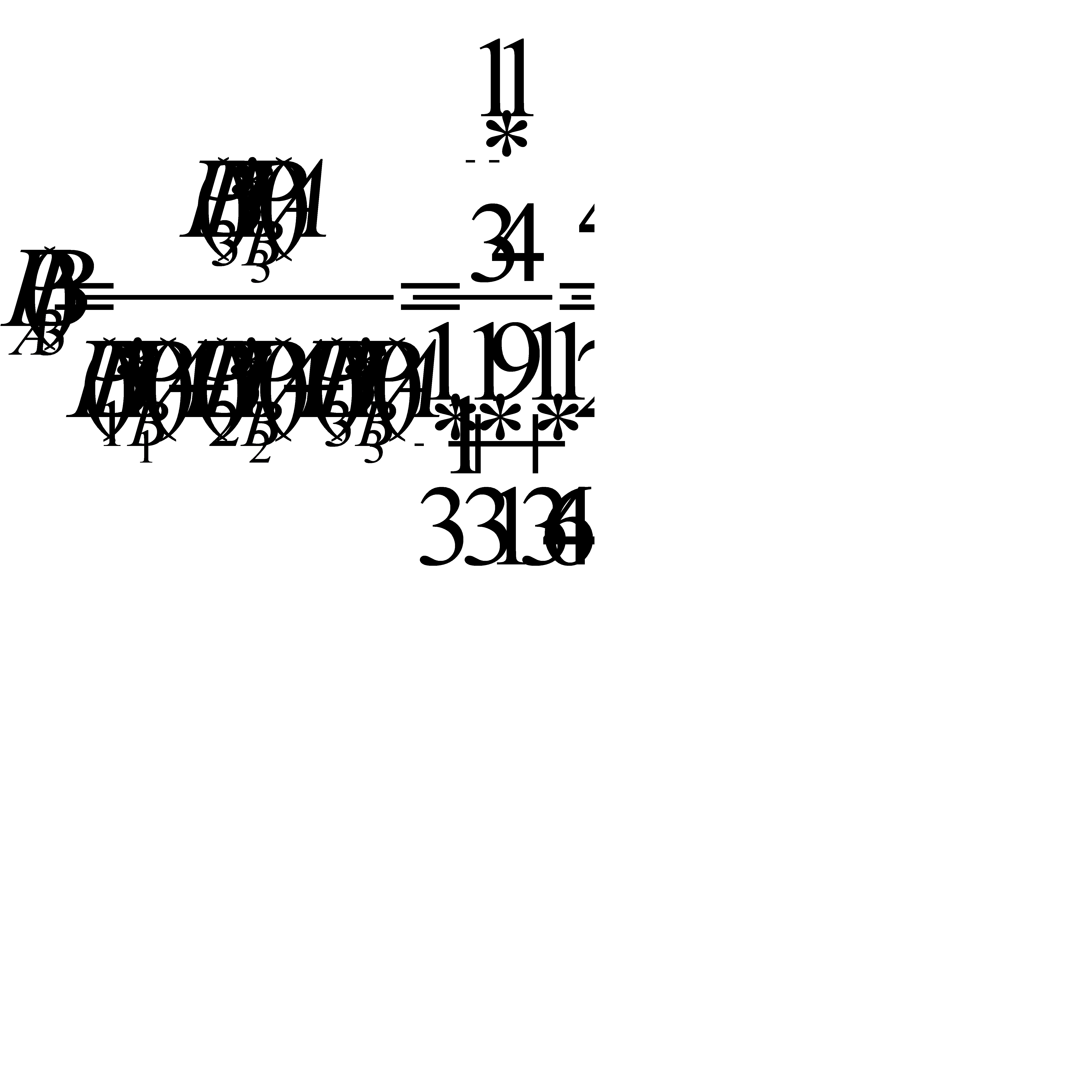
Ответ: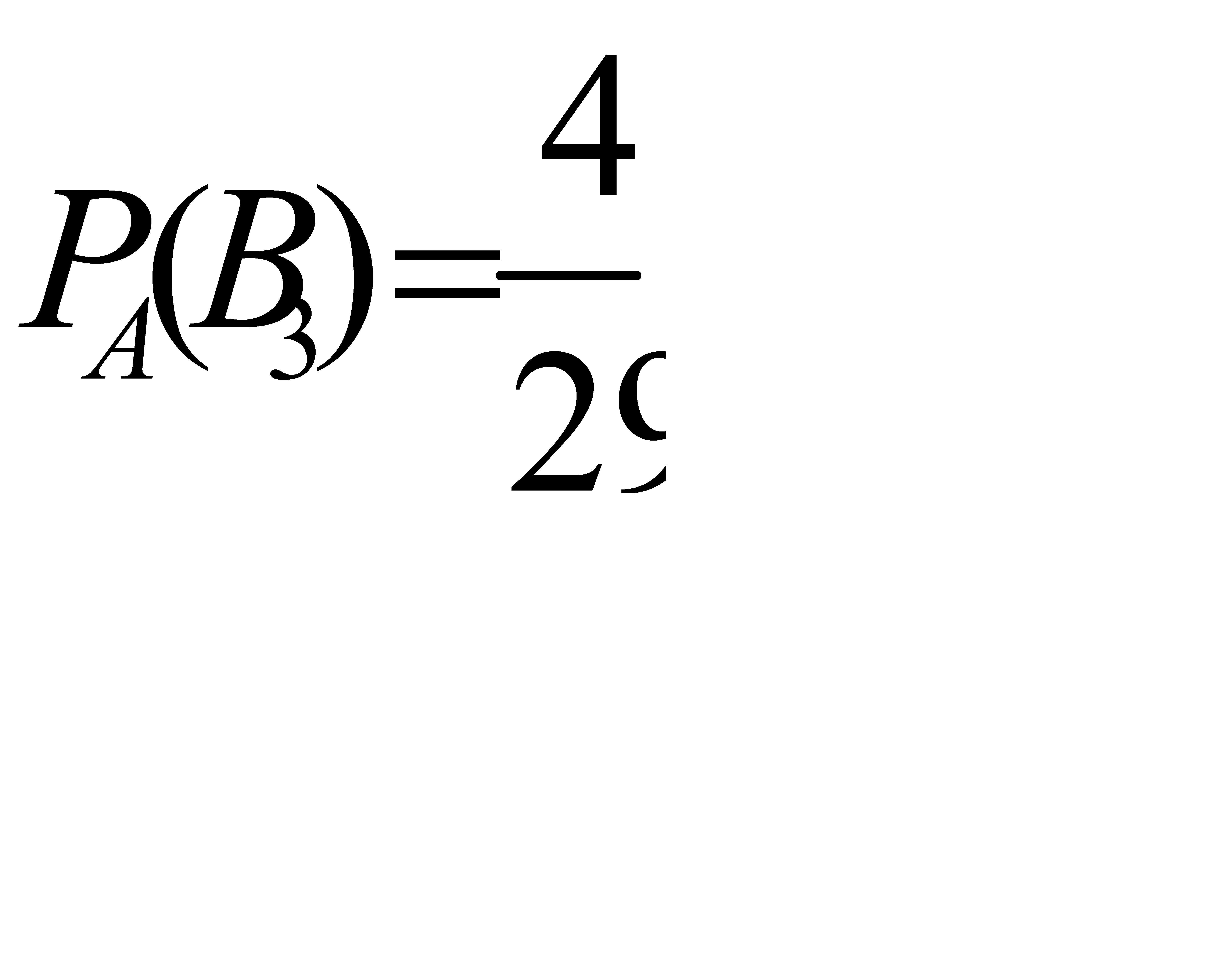

№ 106 Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны , , .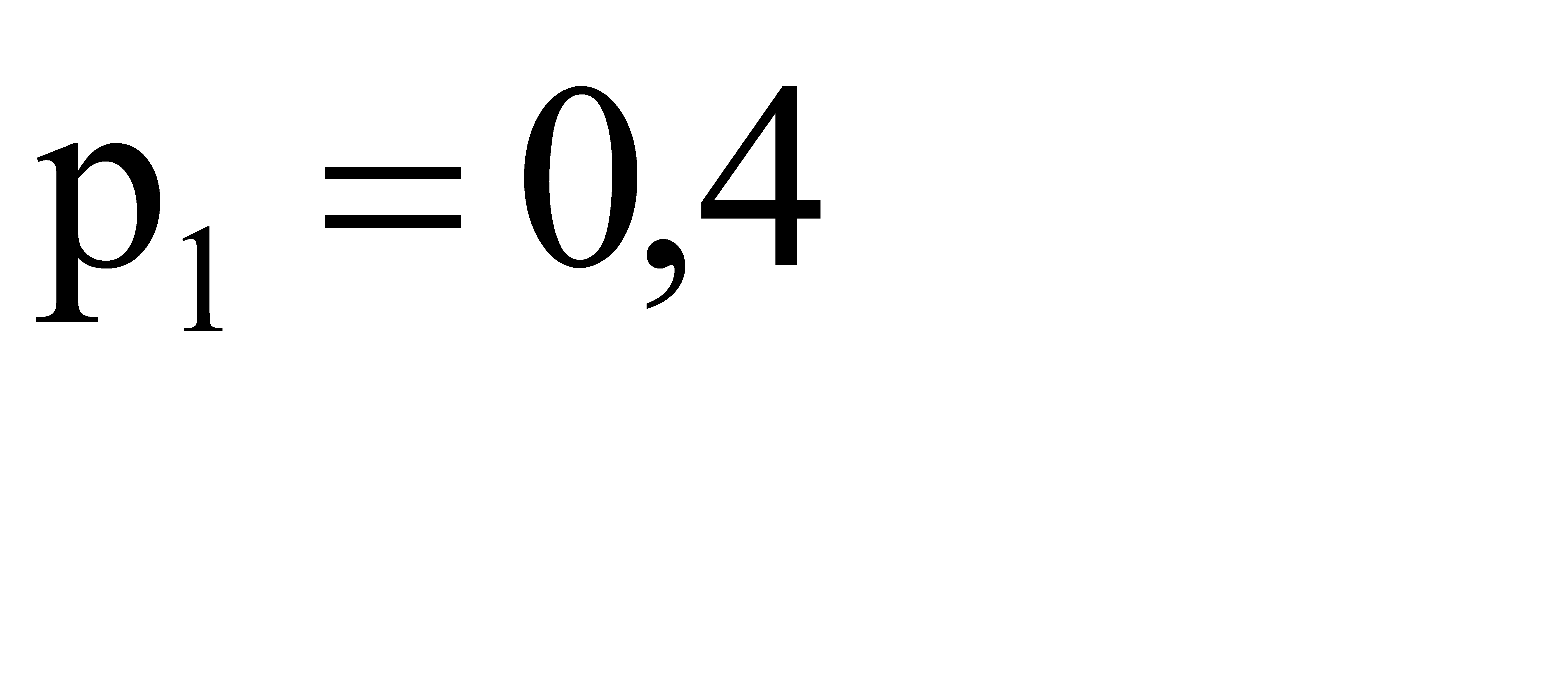

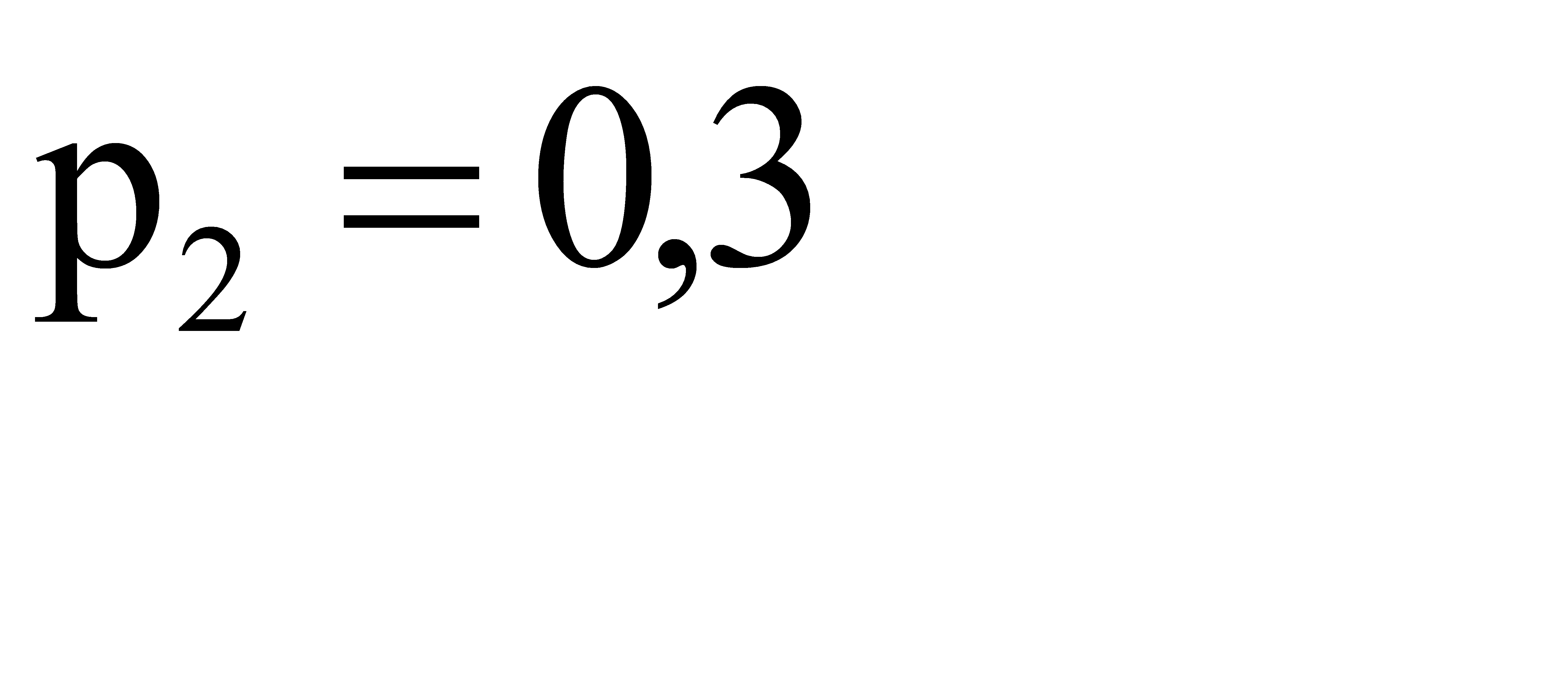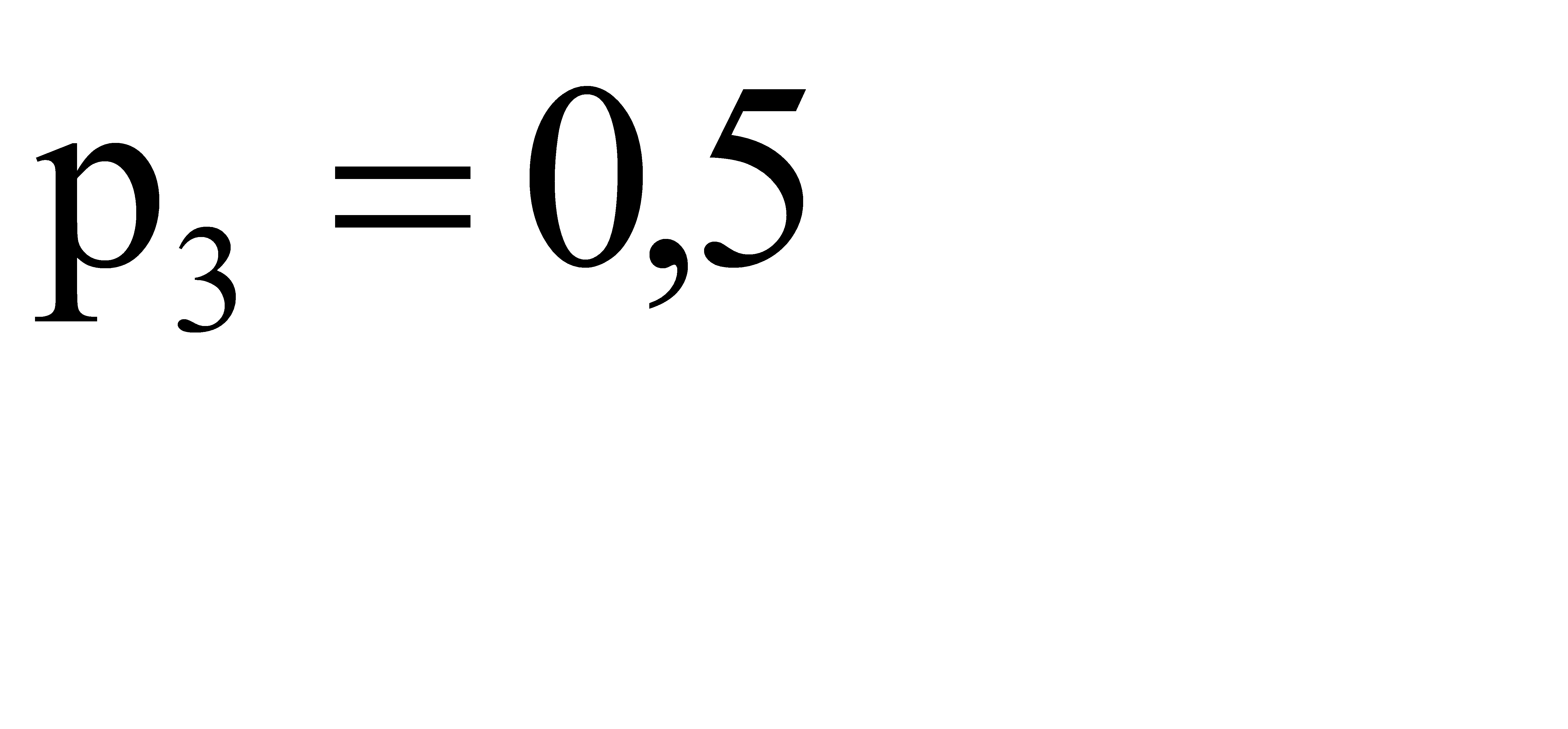Решение:

Обозначим через A событие- два орудия попали в цель. Сделаем два предположения: - орудие не попало в цель.

По условию 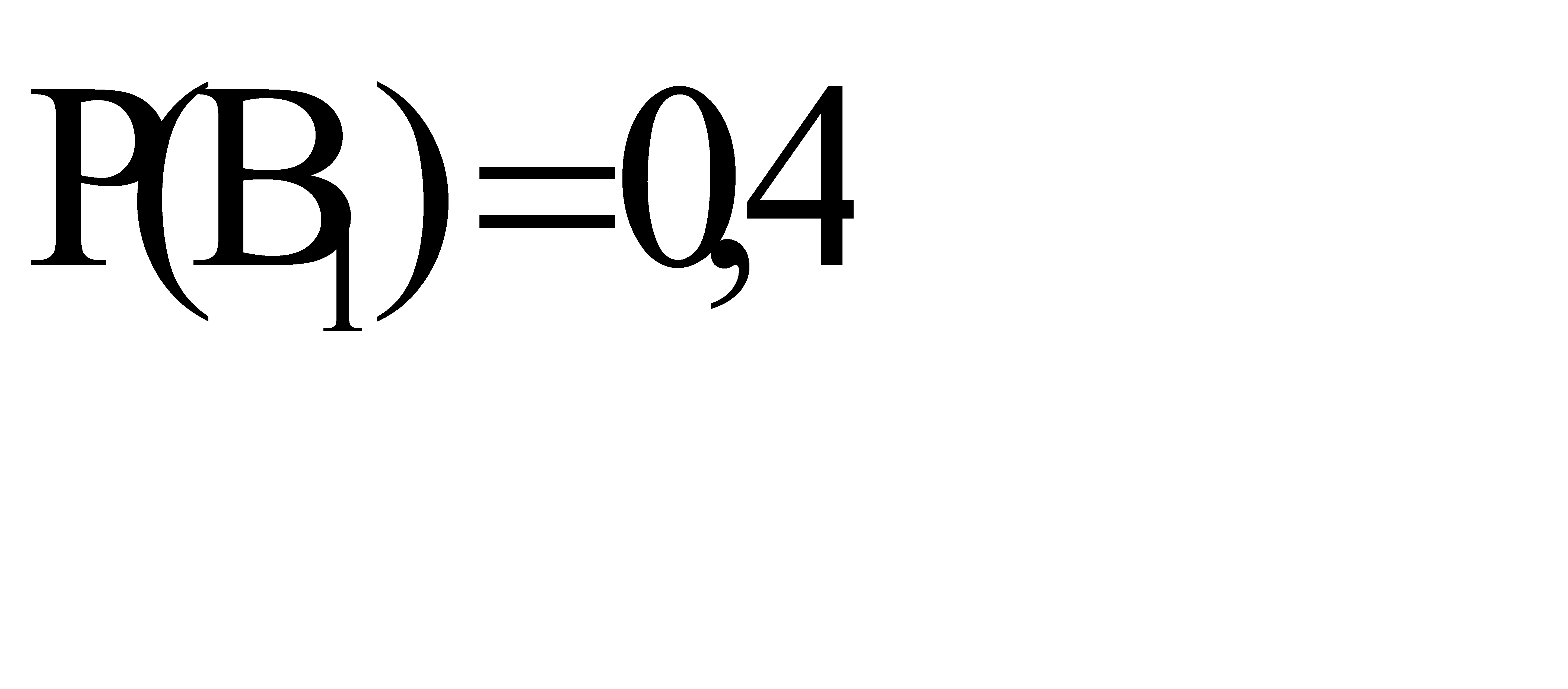, следовательно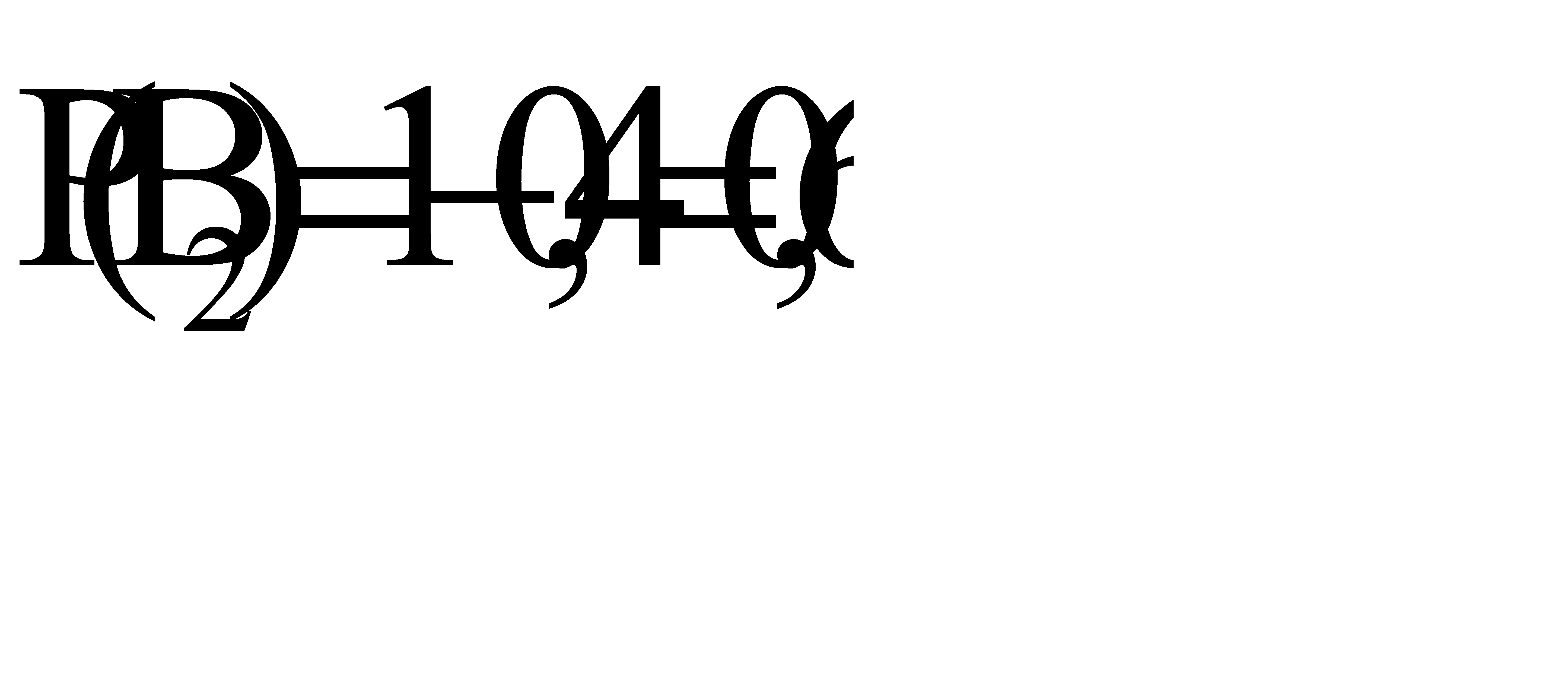

Найдем условную вероятность , т.е. вероятность того, что в цель попало 2 снаряда, причем один из них послан первым орудием и, следовательно, второй - либо вторым орудием, либо третьим. Эти два события несовместны, поэтому применима теорема сложения:

.

Найдем условную вероятность , т.е. вероятность того, что в цель попало два снаряда, причем первое орудие дало промах. Другими словами найдем вероятность того, что второе и третье орудие попали в цель. Эти два события независимы, поэтому применима теорема умножения:

Искомая вероятность того, что первое орудие дало попадание, по формуле Бейеса равна:

.

Ответ: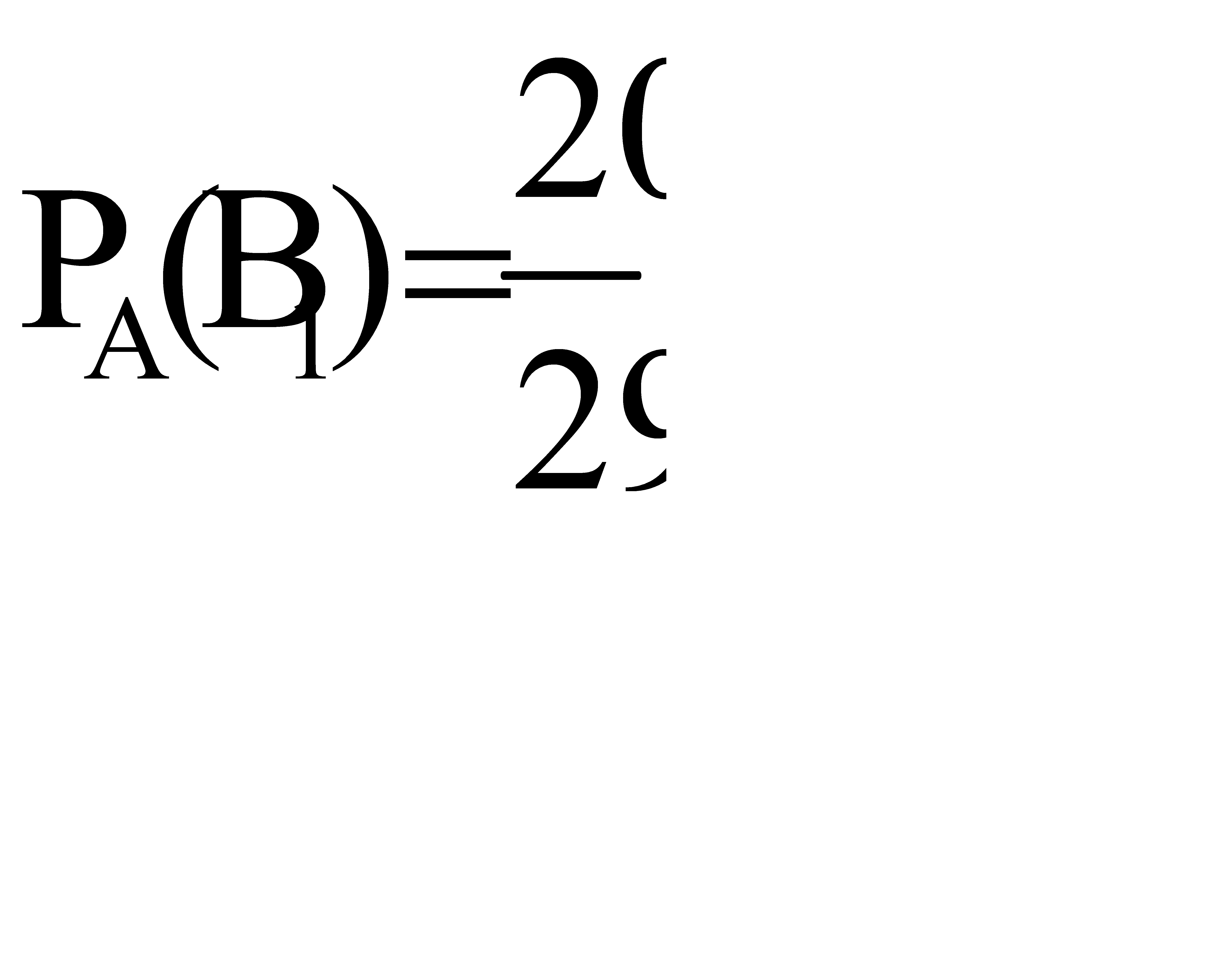

№ 108 Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6, 0,5 и 0,4.

Решение.

Обозначим через А событие – две пули поразили мишень. Сделаем два предположения (гипотезы): В1 – третий стрелок поразил мишень; В2 – третий стрелок не попал в мишень.

По условию, Р(В1) = 0,4; следовательно (событие В2 противоположно событию В1),

Р(В2) = 1 – 0,4 = 0,6.

Найдем условную вероятность РВ1(А), т.е. вероятность того, что мишень поразили две пули, причем одна из них принадлежит третьему стрелку и, следовательно, вторая – либо первому стрелку (при этом второй не попал), либо второму стрелку (при этом первый не попал). Эти два события несовместны, поэтому применима теорема сложения:

РВ1(А) = p1∙q2 + p2∙q1 = 0,6∙0,5 + 0,5∙0,4 = 0,5.

Найдем условную вероятность РВ2(А), т.е. вероятность того, что мишень поразили две пули, причем третий стрелок промахнулся. Другими словами, найдем вероятность того, что первый и второй стрелки поразили мишень. Эти два события независимы, поэтому применима теорема умножения:

РВ2(А) = p1∙p2 = 0,6∙0,5 = 0,3.

Искомая вероятность того, что третий стрелок поразил мишень, по формуле Бейеса равна

РА(В1) = Р(В1)∙РВ1(А)/[ Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А)] = 0,4∙0,5/( 0,4∙0,5 + 0,6∙0,3 ) = 10/19.

Ответ: 10/19.

№ 108 Два из трех независимо работающих элементов вычислительного устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0,2; 0,4 и 0,3.

Решение.

Обозначим через А событие – отказали два элемента. Можно сделать следующие предположения (гипотезы):

В1 - отказали первый и второй элементы, а третий элемент исправен, причем (поскольку элементы работают независимо, применима теорема умножения)

Р(В1) = p1∙p2∙q3 = 0,2∙0,4∙0,7 = 0,056;

В2 - отказали первый и третий элементы, а второй элемент исправен, причем

Р(В2) = p1∙p3∙q2 = 0,2∙0,3∙0,6 = 0,036;

В3 - отказали второй и третий элементы, а первый - исправен, причем

Р(В3) = p2∙p3∙q1 = 0,4∙0,3∙0,8 = 0,096;

В4 - отказал только один элемент; В5 - отказали все три элемента; В6 - ни один из элементов не отказал.

Вероятности последних трех гипотез не вычислены, так как при этих гипотезах событие А (отказали два элемента) невозможно и значит условные вероятности РВ4(А), РВ5(А) и РВ6(А) равны нулю, следовательно, равны нулю и произведения Р(В4)∙РВ4(А), Р(В5)∙РВ5(А) и Р(В6)∙РВ6(А) при любых значениях вероятностей гипотез В4, В5 и В6.

Поскольку при гипотезах В1, В2 и В3 событие А достоверно, то соответствующие условные вероятности равны единице:

РВ1(А) = РВ2(А) = РВ3(А) = 1.

По формуле полной вероятности, вероятность того, что отказали два элемента, равна

Р(А) = Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А) + Р(В3)∙РВ3(А) + Р(В4)∙РВ4(А) + Р(В5)∙РВ5(А) + Р(В6)∙РВ6(А) = 0,056 + 0,036 + 0,096 = 0,188.

По формуле Бейеса, искомая вероятность того, что отказали первый и второй элементы,

РА(В1) = Р(В1)∙Р_В1(А)/ Р(А) = 0,056/0,188 = 0,3.

Ответ: 0,3.

Кравченко Антонина.

№109.Две из четырех независимо работающих ламп прибора отказали. Найти вероятность того, что отказали первая и вторая лампы, если вероятности отказа первой, второй, третьей и четвертой ламп соответственно равны 0,1, 0,2, 0,3 и 0,4.

Решение:

Обозначим через А событие – отказали две лампы. Можно сделать следующие предположения (гипотезы):

В1 - отказали первая и вторая лампы, а третья и четвертая лампы исправны, причем (поскольку лампы работают независимо, применима теорема умножения)

Р(В1) = p1∙p2∙q3∙q4 = 0,1∙0,2∙0,7∙0,6 = 0,0084;

В2 - отказали первая и третья лампы, а вторая и четвертая исправны, причем

Р(В2) = p1∙q2∙p3 ∙q4 = 0,1∙0,8∙0,3∙0,6 = 0,0144;

В3 - отказали первая и четвертая лампы, а вторая и третья - исправны, причем

Р(В3) = p1∙q2∙q3∙p4 = 0,1∙0,8∙0,7∙0,4 = 0,0224;

В4 - отказали вторая и третья лампы, а первая и четвертая - исправны, причем

Р(В4) = q1∙p2∙p3∙q4 = 0,9∙0,2∙0,3∙0,6 = 0,0324;

В5 - отказали вторая и четвертая лампы, а первая и третья - исправны, причем

Р(В5) = q1∙p2∙q3∙p4 = 0,9∙0,2∙0,7∙0,4 = 0,0504;

В6 - отказали третья и четвертая лампы, а первая и вторая - исправны, причем

Р(В6) = q1∙q2∙p3∙p4 = 0,9∙0,8∙0,3∙0,4 = 0,0864;$

В7 – отказала только одна лампа; В8 - отказали три лампы; В9 - отказали все четыре лампы и В10 – все лампы остались исправны.

Вероятности последних четырех гипотез не вычислены, так как при этих гипотезах событие А (отказали две лампы) невозможно и значит условные вероятности РВ7(А), РВ8(А), РВ9(А) и РВ10(А) равны нулю, следовательно, равны нулю и произведения Р(В7)∙РВ7(А), Р(В8)∙РВ8(А), Р(В9)∙РВ9(А) и Р(В10)∙РВ10(А) при любых значениях вероятностей гипотез В7, В8, В9 и В10.

Поскольку при гипотезах В1 – В6 событие А достоверно, то соответствующие условные вероятности равны единице:

РВ1(А) = РВ2(А) = РВ3(А) = РВ4(А) = РВ5(А) = РВ6(А) = 1.

По формуле полной вероятности, вероятность того, что отказали две лампы, равна

Р(А) = Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А) + Р(В3)∙РВ3(А) + Р(В4)∙РВ4(А) + Р(В5)∙РВ5(А) + Р(В6)∙РВ6(А) + Р(В7)∙РВ7(А) + Р(В8)∙РВ8(А) + Р(В9)∙РВ9(А) + Р(В10)∙РВ10(А) = 0,0084 + 0,0144 + 0,0224 + 0,0324 + 0,0504 + 0,0864 = 0,2144.

По формуле Бейеса, искомая вероятность того, что отказали первая и вторая лампы, равна