Свойства и графики тригонометрических функций
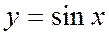
1. Область определения – множество всех действительных чисел.
2. Область изменения (множество значений) – промежуток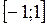 
.
3. Функция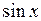 
нечетная: 
.
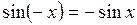4. Функция 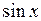периодическая. Наименьший положительный период равен 2p: 
.
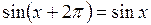5. Нули функции: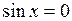 
при 
.
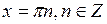6. Промежутки знакопостоянства:
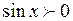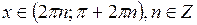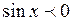при 
,
при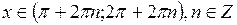 
.
7. Функция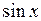
возрастает при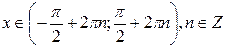 
и убывает при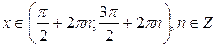 
.
8. Функция 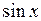принимает
минимальные значения, равные -1, при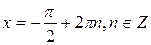 
,
и максимальные значения, равные 1, при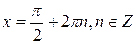 
.
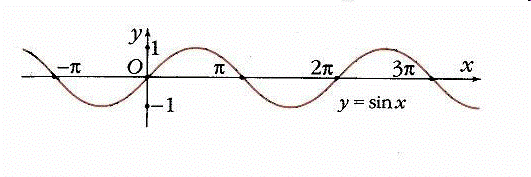
График функции 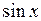называют синусоидой.
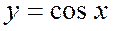
1. Область определения – множество всех действительных чисел.
2. Область изменения (множество значений) – промежуток .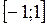
3. Функция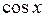 
четная: 
.
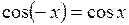4. Функция 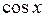периодическая. Наименьший положительный период равен 2p: 
.
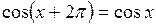5. Нули функции: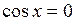 
при 
.
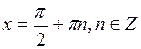6. Промежутки знакопостоянства:
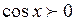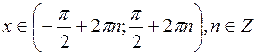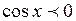при 
,
при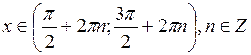 
.
7. Функция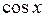
возрастает при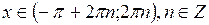 
и убывает при .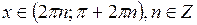
8. Функция 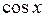принимает
минимальные значения, равные -1, при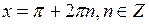 
,
и максимальные значения, равные 1, при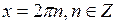 
.
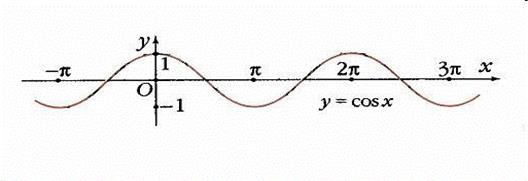
График функции 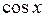также называют синусоидой.
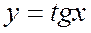
1. Область определения – множество всех действительных чисел, кроме чисел .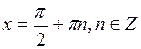
2. Область изменения (множество значений) – множество всех действительных чисел.
3. Функция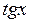 
нечетная: 
.
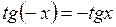4. Функция 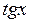периодическая. Наименьший положительный период равен p: 
.
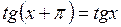5. Нули функции: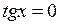 
при .
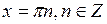6. Промежутки знакопостоянства:
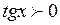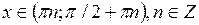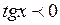при 
,
при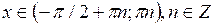 
.
7. Функция 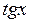возрастает в каждом из промежутков 
.
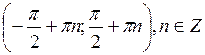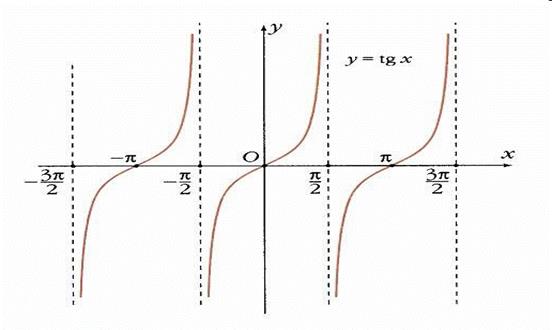
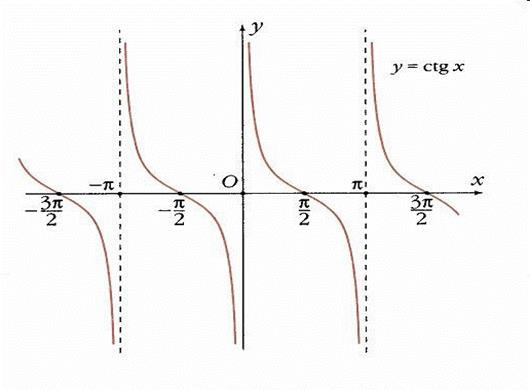
График функции 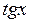называют тангенсоидой.
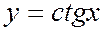
1. Область определения – множество всех действительных чисел, кроме чисел .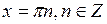
2. Область изменения (множество значений) – множество всех действительных чисел.
3. Функция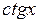 
нечетная: 
.
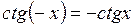4. Функция 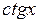периодическая. Наименьший положительный период равен p: 
.
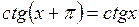5. Нули функции: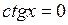 
при 
.
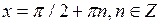6. Промежутки знакопостоянства:
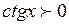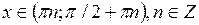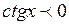при ,
при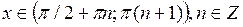 
.
7. Функция 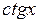убывает в каждом из промежутков 
.
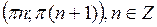Обратные тригонометрические функции
Теорема о корне
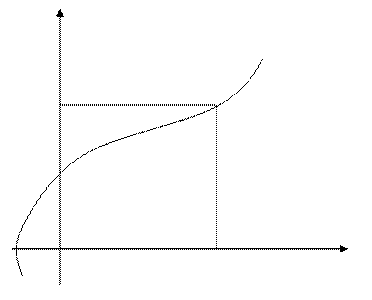Пусть функция 
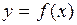монотонна (возрастает или убывает) на промежутке I, число a – любое из значений, принимаемых f на этом промежутке. Тогда уравнение 
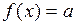имеет единственный корень b в промежутке I.
у
y=f(x)
a
0 b x
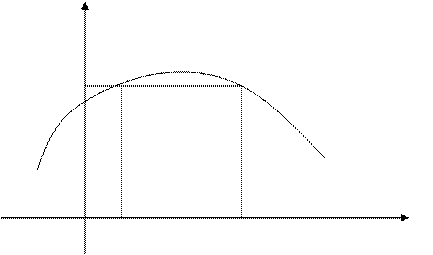
Доказательство: Докажем единственность корня уравнения .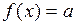
Пусть существует с – еще один корень уравнения .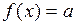
Т.е.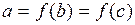 
.
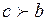, либо 
.
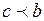Т.к.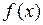 
монотонна, то 
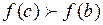, либо 
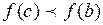, что противоречит предположению.
Следовательно, b - единственный корень.
y
y=f(x)
a
0 b c x
Функция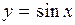 
возрастает на отрезке 
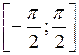и принимает все значения от -1 до 1. Следовательно, по теореме о корне, для любого числа a, такого, что 
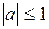, в промежутке 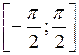существует единственный корень b уравнения 
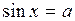. Это число b называют арксинусом числа a и обозначают 
.
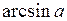Арксинусом числа a называется числоиз отрезка 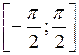, синус которого равен a.