Замена распределенных сил эквивалентными сосредоточенными

В задачах встречаются системы параллельных сил, распределенных по некоторому закону вдоль прямолинейного стержня (рис.1.33).

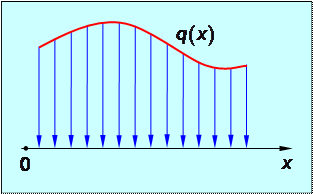
Рис.1.33

Такие распределенные силы характеризуются интенсивностью q, равной величине силы, приходящейся на единицу длины нагруженного отрезка (например, погонный вес балки как элемента строительной конструкции). В общем случае интенсивность является некоторой функцией q(x) координаты x, отсчитываемой вдоль нагруженного отрезка.

Интенсивность измеряется в системе единиц СИ в ньютонах, деленных на метры (Н/м).

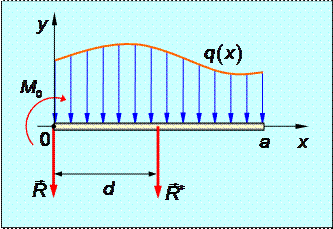
Рис.1.34

Рассмотрим систему параллельных сил, распределенных по произвольному закону q(x) вдоль прямолинейного отрезка длиной a и направленных

перпендикулярно этому отрезку (рис.1.33).

Величина главного вектора 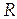и главный алгебраический момент M_O относительно центра (т. О) определяются суммированием (интегрированием) элементарных бесконечно малых сил q(x)·dx моментов x·q(x)·dx по всей длине нагруженного участка:

.

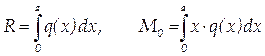Если приложить главный вектор 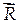в точке стержня, удаленной от О на расстоянии 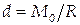(рис.1.34), то его момент относительно т.О станет равным главному алгебраическому моменту М₀. Это означает, что приложенный в этой точке один вектор 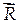* определяет такой же главный вектор и главный алгебраический момент системы. Таким образом, системы эквивалентны. Следовательно, приложенный в этой точке главный вектор 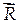* является равнодействующей силой, или, как принято говорить, сосредоточенной силой, эквивалентной исходной распределенной нагрузке.

Итак, формулы для оценки эквивалентной сосредоточенной силы и точки её приложения:

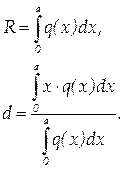(1.36)

Воспользуемся полученными формулами для двух часто встречающихся случаев: равномерно и линейно распределенные нагрузки.

Равномерно распределенная нагрузка (рис.1.35).

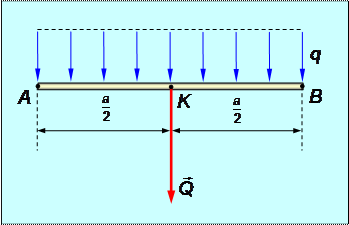
Рис.1.35

Здесь интенсивность постоянна: q = const. Распределенную нагрузку можно заменить сосредоточенной силой 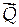, равной произведению интенсивности на длину отрезка и приложенной к середине нагруженного участка:

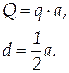(1.37)

Силы, распределенные по линейному закону (рис.1.36).

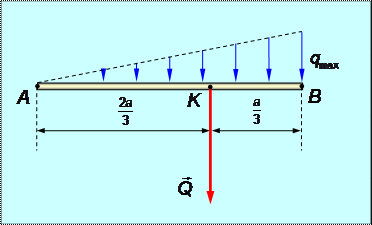
Рис.1.36

Для такой системы сил интенсивность q меняется от нуля до максимального значения q_max по линейному закону.

Эквивалентная сосредоточенная сила 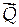этой системы приложена в точке, делящей нагруженный участок в соотношении 2 : 1 (рис.1.36) и равна:

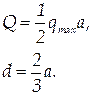(1.38)

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Определите величину и точку приложения равномерно распределенной нагрузки.

2. Определите величину и точку приложения линейно распределенной нагрузки.

3. Какую размерность имеет погонный вес?