Матрицы и действия над ними
Понятие о матрице
Таблица чисел аik вида
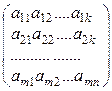 , (5.1)
, (5.1)
состоящая из m строк и n столбцов называется матрицей размера m × n. Числа аik называются её элементами. Если m ¹ n, то матрица называется прямоугольной.Если же m = n, то матрица называется квадратной.В частности, если m = 1, n > 1, то матрица (а11 а12 … а1n) называется матрицей-строкой. Если же m > 1, n = 1, то матрица называется матрицей-столбцом.
Число строк в квадратной матрице называют порядком такой матрицы. Например, матрица 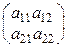 есть квадратная матрица второго порядка, а матрица
есть квадратная матрица второго порядка, а матрица 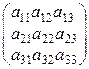 есть квадратная матрица третьего порядка.
есть квадратная матрица третьего порядка.
Матрицы будем обозначать большими латинскими буквами. Две матрицы A и B называются равными (А = В), если они одинакового размера и их соответствующие элементы равны. Так, если А = 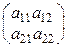 , В =
, В = 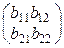 и а11 = b11, a12 = b12, a21 = b21, a22 = b22, то А = В.
и а11 = b11, a12 = b12, a21 = b21, a22 = b22, то А = В.
Алгебраические преобразования матриц
Сложение и вычитание матриц
Складывать и вычитать можно только матрицы одинакового размера.
Определение 5.1. Суммойдвух матриц А и В одинакового размера m × n называется матрица С размера m × n, элементы которой равны сумме соответствующих элементов матриц А и В. Обозначается : А + В = С.
Пример. 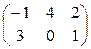 +
+ 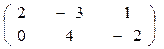 =
= 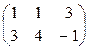
Определение 5.2.Матрица О размера m × n, элементы которой все равны нулю, называется нулевой матрицей.
Определение 5.3. Разностью двух матриц А и В размера m × n называется матрица С размера m × n такая, что А = В + С. Обозначается : А – В = С. Из определения следует, что элементы матрицы С равны разности соответствующих элементов матриц А и В.
Пример. 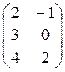 –
– 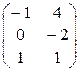 =
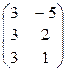
= 
Свойства сложения матриц.
1. Сложение матриц коммутативно, т. е. А + В = В + А для любых матриц А и В размера m × n.
2. Сложение матриц ассоциативно, т. е. (А + В) + С = А + ( В + С) для любых матриц А, В, С одинакового размера.
3. А + О = О + А = А для любой матрицы A размера, совпадающей с размером нулевой матрицы О.
Умножение матрицы на число
Определение 5.4. Произведением матрицы A на число αназывается матрица αА, элементы которой равны произведению числа α на соответствующие элементы матрицы А.
Пример.Вычислите 2А – 3В, если A = 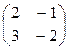 , В =
, В = 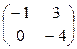 .
.
2А – 3В = 2 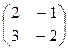 – 3
– 3 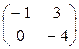 =
= 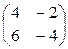 –
– 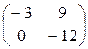 =
= 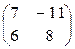 .
.
Умножение матриц
Определение 5.5. Произведениемматрицы А размерности m × n и матрицы В размерности n × k, элементы которой сij вычисляются как сумма произведений соответствующих элементов аil i-й строки матрицы А и элементов blj j-го столбца матрицы В, т. е.
cij = ai1b1j + ai2b2j + … + ainbnj, i 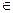 {1, 2, …, m}; j
{1, 2, …, m}; j 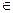 {1, 2, …, k}.
{1, 2, …, k}.
Пример.
1) 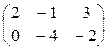
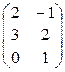 =
= 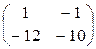 ; 2)
; 2) 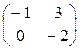
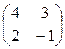 =
= 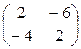 ;
;
3) 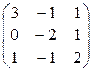
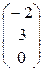 =
= 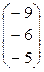 .
.
Определение 5.6.Квадратная матрица порядка n вида называется единичной матрицей и обозначается En.
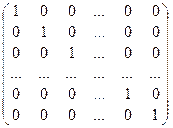
Свойства умножения матриц
1. Умножение матриц некоммутативно, т. е. AB ¹ BA.
2. Умножение матриц ассоциативно, т. е. A(BC) = (AB)C, если такие произведения существуют.
3. Если A – матрица размера m × n, B – матрица размера n × k, то A × En = A, En × B = B.
Транспонирование матриц
Определение 5.7.Если в матрице
А = 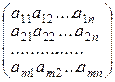
сделать все строки столбцами с тем же номером, то получим матрицу
Аt = 
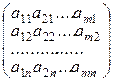
которую называют транспонированнойк матрице А.
Свойства транспонирования матриц
1. (At)t = A.
2. (A + B)t = At + Bt.
3. (AB)t = BtAt .
4. ( 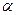 A) t =
A) t = 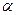 At .
At .
Пример.Найти 2At + (AB)t, если А = 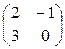 , В =
, В = 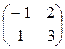 .
.
2Аt + (AB)t = 2 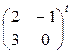 +
+ 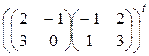 = 2
= 2 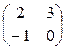 +
+ 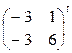 =
= 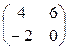 +
+
+ 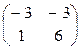 =
= 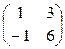 .
.
