Тема. Розв’язування задач на складання рівнянь ліній другого порядку:гіперболи, параболи
Мета роботи: навчитись складати рівняння кривих другого порядку за виглядом рівнянь ліній досліджувати їх особливості.
Наочне забезпечення та обладнання:
1. Інструкційні картки;
2. Приклади задач;
3. Роздаткові матеріали: опорні конспекти “Основні формули аналітичної геометрії”
4. Обчислювальні засоби.
 Теоретичні відомості про гіперболу
Теоретичні відомості про гіперболу
Гіперболою називається геометричне місце точок модуль різниці відстаней для кожної з яких до двох даних фіксованих точок (фокусів) є величина стала, менша за відстань між фокусами і дорівнює 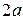 . Найпростіше рівняння гіперболи:
. Найпростіше рівняння гіперболи:
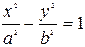 ,
,
де 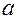 - дійсна піввісь гіперболи,
- дійсна піввісь гіперболи, 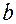 - уявна піввісь.
- уявна піввісь.
Якщо 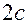 - відстань між фокусами, то
- відстань між фокусами, то 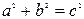 . При
. При 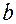 =
= 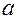 гіпербола називається рівносторонньою, її рівняння має вигляд:
гіпербола називається рівносторонньою, її рівняння має вигляд: 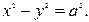 Фокуси гіперболи знаходяться на її дійсній осі. Ексцентриситет гіперболи – це відношення фокусної відстані до довжини дійсної осі:
Фокуси гіперболи знаходяться на її дійсній осі. Ексцентриситет гіперболи – це відношення фокусної відстані до довжини дійсної осі: 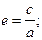
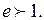
Асимптоти гіперболи – прямі, що задаються рівняннями 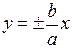 .
.
Якщо фокуси гіперболи лежать на осі 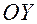 , то її рівняння має вигляд:
, то її рівняння має вигляд:
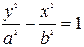 або
або 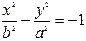 ,
,
а рівняння асимптот такої гіперболи 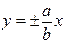 .
.
Рівняння рівносторонньої гіперболи з фокусами на осі 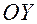 має вигляд:
має вигляд: 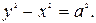
Гіперболи :
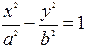 і
і 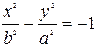
називаються спряженими.
В усіх задачах на гіперболу передбачено, що осі симетрії гіперболи співпадають з осями координат.
Задача №1. Скласти рівняння гіперболи, що має асимптотами прямі 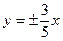 і проходить через точку (-5;2).
і проходить через точку (-5;2).
Задача №2. Скласти рівняння гіперболи, якщо її вершини лежать в точках 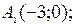
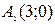 і фокуси в точках
і фокуси в точках 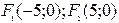 .
.
Задача № 3. Дано рівняння гіперболи 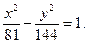 Знайти координати її вершин і фокусів.
Знайти координати її вершин і фокусів.

Теоретичні відомості про параболу
Параболою називається геометричне місце точок, кожна з яких однаково віддалена від заданої фіксованої точки (фокуса) і від заданої фіксованої прямої (директриси). Найпростіше рівняння параболи має вигляд: 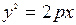 , де
, де 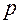 - параметр, тобто відстань між директрисою та фокусом. Рівняння директриси
- параметр, тобто відстань між директрисою та фокусом. Рівняння директриси 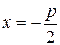 , фокус – це точка
, фокус – це точка 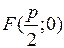 .
.
Є випадки задання параболи:
1) 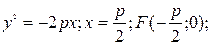
2) 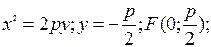
3) 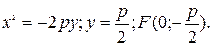
Рівняння парабол зі зміщеною вершиною мають вигляд:
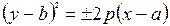 ;
; 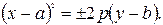
Задача № 4. Скласти рівняння параболи з вершиною в початку координат, знаючи координати фокуса (-2;0).
Задача № 5. Визначити координати вершини і величину параметра параболи, рівняння якої: 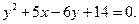 Знайти також координати її фокуса і рівняння директриси параболи
Знайти також координати її фокуса і рівняння директриси параболи
Питання для самоперевірки знань, умінь
1. Що називається гіперболою? Осі гіперболи, фокуси, вершини.
2. Канонічне рівняння гіперболи. Спряжені гіперболи.
3. Яка гіпербола називається рівносторонньою ?
4. Ексцентриситет гіперболи.
5. Рівняння асимптот гіперболи.
6. Що таке парабола? Вершина параболи, фокус, параметр.
7. Що називається директрисою параболи? Рівняння директриси параболи.
8. Як визначити вершину параболи та її параметр, якщо задано рівняння параболи ?
Висновок__________________________________________________
Перевірив викладач ___________ Оцінка ___________ Дата ___________
