Задания для самостоятельной работы.
№6 Вычислить с помощью таблицы интегралов
а) 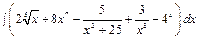 ,
,
б) 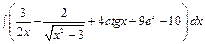 ,
,
в) 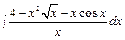 , г)
, г) 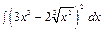 .
.
№7 Найти интегралы методом компенсирующего множителя или введением под знак дифференциала
а) 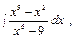 б)
б) 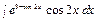 , в)
, в)  ,
,
г) 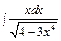 , д)
, д)  , е)
, е)  , ж)
, ж) 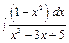 ,
,
з) 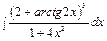 , и)
, и) 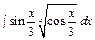 , к)
, к) 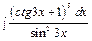 .
.
№8 Найти интегралы методом интегрирования по частям:
а) 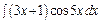 , б)
, б) 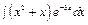 , в)
, в) 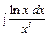 , г)
, г) 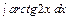 ,
,
д)  е)
е) 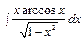 . b)
. b) 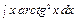
Ответы
Ответы к гл. 3
3.1.1) 24, 2) п(п+1)(п+2), 3)  , 4)
, 4) 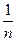 , 5)336, 6) 120,
, 5)336, 6) 120,
7) 4950, 8) 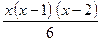 .
.
3. 2. 1) 6;11, 2) 5, 3) 7, 4) 5, 5) 4, 6) 13, 7) 2;3;4;5;6;7;8;9,
8) 5;6;7;8;9;10.
3.3.3) Доказательство. 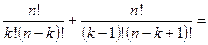
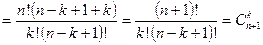 .
.
4) Доказательство. Используем равенство, доказанное
в предыдущем номере. Имеем:
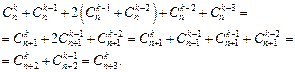
3.4.96. 3. 5.А)125, б) 24. 3. 6.350. 3.7.1605. 3. 8.968.
3.9.720. 3.10.а) 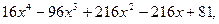
б) 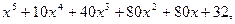 в)
в) 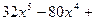
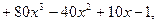 г)
г) 
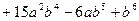 .3.11.1) +3; -3, 2)+2; -2, 3)-2; 0, 4) 0; 2.
.3.11.1) +3; -3, 2)+2; -2, 3)-2; 0, 4) 0; 2.
3.12.1)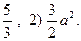 3.14.2) Доказательство. Для п=1 неравенство верно
3.14.2) Доказательство. Для п=1 неравенство верно 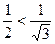 , т.к.
, т.к. 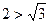 . Пусть неравенство верно для всех номеров п от 1 до к. Докажем, что оно верно и для п = к +1. Имеем:
. Пусть неравенство верно для всех номеров п от 1 до к. Докажем, что оно верно и для п = к +1. Имеем: 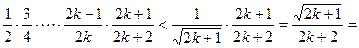
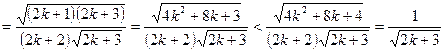 3.14.5) Т.к.
3.14.5) Т.к. 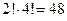 ,
,  и 48>36, то неравенство верно для п =2. Пусть оно верно для всех
и 48>36, то неравенство верно для п =2. Пусть оно верно для всех 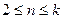 . Докажем, что оно верно и для п = к + 1. Имеем:
. Докажем, что оно верно и для п = к + 1. Имеем:

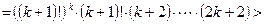
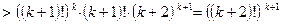 , что и требовалось.
, что и требовалось.
3.16. Т.к. 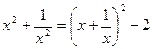 , то
, то 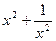 целое и, следовательно, для п = 2 предложение выполняется. Пусть оно выполняется для всех
целое и, следовательно, для п = 2 предложение выполняется. Пусть оно выполняется для всех 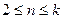 . Докажем, что оно выполняется и для п = к + 1. Имеем:
. Докажем, что оно выполняется и для п = к + 1. Имеем:
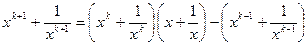 , что и требовалось.
, что и требовалось.
3.18.1) 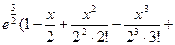
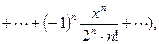 2)
2) 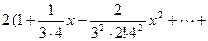
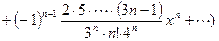 .
.
3.19.1) 0,2594, 2) 2,2359 , 3) 2,547.
3.20.1)—132—42i , 2) 23—5i , 3) 18+i , 4) 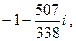
5) 2i—3, 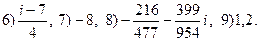
3.21. 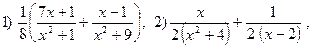
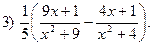
3.22. 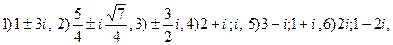
7) –i;--2—i, 8)-1-i;-3-i, 9) 3-3i ;3i-1, 10)3+i;1-2i, 11)-i;1 +2i.
3.23. 
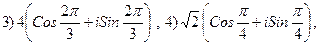
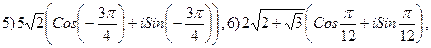
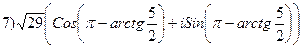 ,
, 
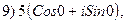
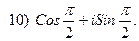
3.24. 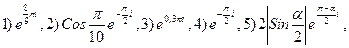
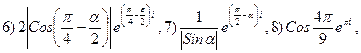
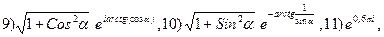
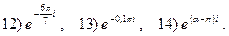
3.25. 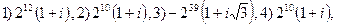
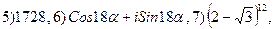
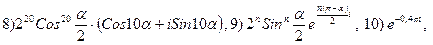
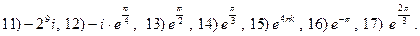
3.26. 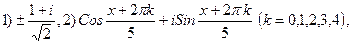
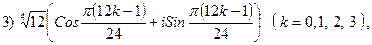
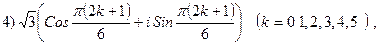
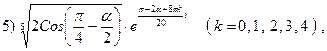
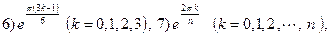


3.27. 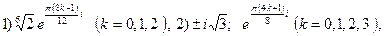

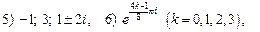
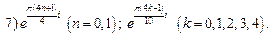
3.28. 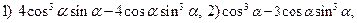
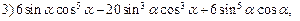
.
Ответы к ИДЗ: Пределы и нелрерывность
Вариант 1. 1.0. 2.-3. 4.-2. 5.0. 6.4. 7. 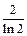 . 8.7. 9.
. 8.7. 9. 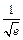 . 10 а.4. 10б.1. 11.-1/6. Вариант 2. 1.
. 10 а.4. 10б.1. 11.-1/6. Вариант 2. 1. 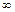 . 2.-1/2. 4.5/4. 5.0. 6.
. 2.-1/2. 4.5/4. 5.0. 6.  . 7.
. 7.  . 8.
. 8. 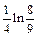 . 9.
. 9. 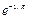 . 10 а.0. 10б.1. 11.-1/6
. 10 а.0. 10б.1. 11.-1/6
Вариант 3. 1.0. 2.-3. 4.-2. 5.0. 6.4. 7. 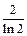 . 8.7. 9.
. 8.7. 9. 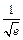 . 10 а.4. 10б.1. 11.–1/6. Вариант 4. 1.-3/2. 2.0. 4.3. 5.-2/3. 6. -16. 7.
. 10 а.4. 10б.1. 11.–1/6. Вариант 4. 1.-3/2. 2.0. 4.3. 5.-2/3. 6. -16. 7. 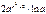 . 8.
. 8.  . 9.e-1/2. 10 а.1. 10б.
. 9.e-1/2. 10 а.1. 10б. 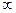 . 11.4.
. 11.4.
Вариант 5. 1. 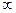 . 2.1/2. 4.3/2. 5.
. 2.1/2. 4.3/2. 5. 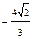 . 6. 1/4. 7.-1/8. 8.-1/2. 9.1/e. 10 а.0. 10б.1. 11.-3/128.
. 6. 1/4. 7.-1/8. 8.-1/2. 9.1/e. 10 а.0. 10б.1. 11.-3/128.
Вариант 6. 1.5/2. 2.3. 4.-1. 5.0,6. 6. -1. 7.1/4. 8.2(1-ln3)/9 . 9. 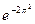 . 10 а.
. 10 а. 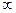 . 10б.1. 11.-13/40.
. 10б.1. 11.-13/40.
Вариант 7. 1. 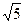 . 2. -1/5. 4.2. 5.0. 6. -2e. 7.-2ln2 8.(-5/2)ln2. 9.
. 2. -1/5. 4.2. 5.0. 6. -2e. 7.-2ln2 8.(-5/2)ln2. 9. 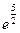 . 10 а.-1/2. 10б.1. 11.-1/72.
. 10 а.-1/2. 10б.1. 11.-1/72.
Вариант 8. 1.0. 2.2/3. 4.3. 5.0. 6. -1/6. 7. 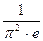 . 8.5ln3-7ln2. 9.2e. 10 а.2/3. 10б.1. 11.-3/4.
. 8.5ln3-7ln2. 9.2e. 10 а.2/3. 10б.1. 11.-3/4.
Вариант 9. 1.0. 2.4/3. 4.0. 5.2,4. 6. 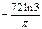 . 7. -2/3π. 8.2. 9.3/7. 10 а. -1/2. 10б.1. 11.-3/4.
. 7. -2/3π. 8.2. 9.3/7. 10 а. -1/2. 10б.1. 11.-3/4.
Вариант 10. 1. 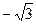 . 2.-1. 4.0. 5.0. 6. -2/3. 7.0. 8.
. 2.-1. 4.0. 5.0. 6. -2/3. 7.0. 8. 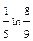 . 9.1. 10 а.
. 9.1. 10 а. 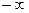 . 10б.e3. 11.-4.
. 10б.e3. 11.-4.
Вариант 11. 1.1/2. 2.1/2. 4.-3. 5.4. 6. -1/2e. 7.8. 8.ln700. 9. 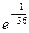 . 10 а.1/64. 10б.
. 10 а.1/64. 10б. 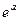 . 11.-1.
. 11.-1.
Вариант 12. 1. 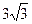 . 2.11/18. 4.0. 5.1,5, 6. 2/5. 7.π/8. 8.3.
. 2.11/18. 4.0. 5.1,5, 6. 2/5. 7.π/8. 8.3.
9. 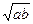 . 10 а.0. 10б.1. 11.11/18.
. 10 а.0. 10б.1. 11.11/18.
Вариант 13. 1.3. 2.1. 4. -1/3. 5. 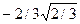 . 6. -10. 7.
. 6. -10. 7. 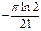 . 8.4. 9.
. 8.4. 9.  . 10 а.0. 10б.0. 11.-13.
. 10 а.0. 10б.0. 11.-13.
Вариант 14. 1.0. 2.1/8. 4.3. 5. 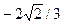 . 6. 1/π. 7.
. 6. 1/π. 7. 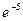 .
.
8.ln25/8. 9. 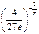 . 10 а.1. 10б.1. 11.-1/3.
. 10 а.1. 10б.1. 11.-1/3.
Вариант 15. 1.4. 2.1/6. 4.-2/3. 5.-4/3. 6. 3/8. 7. 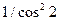 .
.
8.7ln2-5ln3. 9.1/e. 10 а.1. 10б.1. 11.-0,3.
Вариант 16. 1.1. 2.1/6. 4. 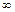 . 5.1/4. 6.
. 5.1/4. 6. 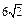 . 7.-8. 8.3-ln2. 9.1/5. 10 а.1/6. 10б.1. 11.-11/24.
. 7.-8. 8.3-ln2. 9.1/5. 10 а.1/6. 10б.1. 11.-11/24.
Вариант 17. 1.2. 2.1/15. 4.-1. 5.-1/2. 6. 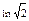 . 7.-2. 8.-9. 9.
. 7.-2. 8.-9. 9. 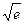 . 10 а.-1/3. 10б.1. 11.-1.
. 10 а.-1/3. 10б.1. 11.-1.
Вариант 18. 1.1. 2.1/5. 4.-2/5. 5.-1/2. 6. 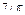 . 7.
. 7. 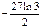 . 8.5ln4-2ln9. 9.
. 8.5ln4-2ln9. 9. 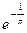 . 10 а.
. 10 а. 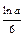 . 10б.1. 11.-3.
. 10б.1. 11.-3.
Вариант 19. 1.-2. 2.-3. 4.1/3. 5.4/3. 6. -1/4. 7. 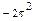 . 8.ln12+3ln5. 9.9. 10 а.2. 10б.1. 11.1/12
. 8.ln12+3ln5. 9.9. 10 а.2. 10б.1. 11.1/12
Вариант 20. 1.1. 2.-1. 4.3. 5. 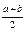 . 6.
. 6. 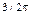 . 7.0. 8.
. 7.0. 8. 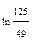 . 9.
. 9. 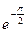 . 10 а.1. 10б.
. 10 а.1. 10б. 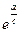 . 11.1/16
. 11.1/16
Вариант 21. 1.1. 2.3/2. 4.1/3. 5.5/2. 6.-2/3. 7.1/2. 8.6. 9. 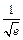 . 10 а.-2. 10б.1. 11.-1.
. 10 а.-2. 10б.1. 11.-1.
Вариант 22. 1. 1. 2.5/2. 4.2. 5.1. 6.7/2. 7. 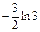 . 8.5. 9.e21/2. 10 а.0. 10б.0. 11.-8/3
. 8.5. 9.e21/2. 10 а.0. 10б.0. 11.-8/3
Вариант 23. 1.-2. 2.-7/2. 4.2. 5.1/3. 6.1/12. 7.  . 8.
. 8. 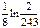 . 9.
. 9.  . 10 а.-2. 10б.е. 11.-8/16
. 10 а.-2. 10б.е. 11.-8/16
Вариант 24. 1.2. 2.5/4. 4.-9. 5.-1/3. 6.-3. 7.2ln23. 8.2ln42. 9.e-4/9. 10 а.1. 10б. 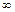 . 11.-1/4.
. 11.-1/4.
Вариант 25. 1.2. 2. 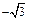 . 4.-7/8. 5.2/27. 6. -5/3. 7.
. 4.-7/8. 5.2/27. 6. -5/3. 7. 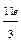 . 8.-1. 9.
. 8.-1. 9. 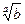 . 10 а.0. 10б.1. 11.-5
. 10 а.0. 10б.1. 11.-5
Вариант 26. 1.-1. 2. 2/3. 4.-5/8. 5.-11/4. 6.1/8. 7. 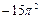 . 8. 2. 9. e-3 . 10 а.-1/2. 10б.1. 11.2.
. 8. 2. 9. e-3 . 10 а.-1/2. 10б.1. 11.2.
Вариант 27. 1.-1. 2.5/4. 4.10/3. 5.9/2. 6.50. 7. 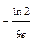 . 8.
. 8. 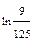 . 9.e1/3. 10 а.-1/3. 10б.1. 11.2.
. 9.e1/3. 10 а.-1/3. 10б.1. 11.2.
Вариант 28. 1.-3/2. 2.3. 4. 3/2. 5.-1/8. 6.-1. 7. 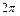 . 8.
. 8.  . 9.e2. 10 а.5/8. 10б.1. 11.-2
. 9.e2. 10 а.5/8. 10б.1. 11.-2
Вариант 29. 1.2. 2.1/12. 4.3/2. 5.2/3. 6.3/2. 7. 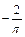 . 8.-5/4. 9.
. 8.-5/4. 9. 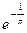 . 10 а.
. 10 а. 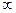 . 10б.
. 10б. 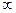 . 11.-27/4.
. 11.-27/4.
Вариант 30. 1. 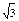 . 2.
. 2.  . 4.0. 5.
. 4.0. 5. 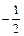 . 6.6. 7.
. 6.6. 7. 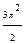 . 8.2ln7-3. 9.
. 8.2ln7-3. 9. 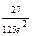 . 10 а.
. 10 а. 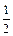 . 10б.1. 11.
. 10б.1. 11. 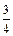 .
.
Литература
1. Берман Г.Н. Сборник задач по курсу математического анализа.  М.: Наука, 1997.
М.: Наука, 1997.
2. Демидович Б.П. Сборник задач и упражнений по математическому анализу.  М.: Наука, 1997.
М.: Наука, 1997.
3.. Виноградова И.А, Олехник С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу.  М.: Наука, 1986.
М.: Наука, 1986.
4. Кузнецов Л.А. Сборник заданий по высшей математике.  М.: Высшая школа, 1990.
М.: Высшая школа, 1990.
5. Сборник индивидуальных заданий по высшей математике,
ч. 1, Под ред. А.П. Рябушко.  Минск: Высшая школа, 1990.
Минск: Высшая школа, 1990.
6. Клетеник Д.В. Сборник задач по аналитической геометрии. 
М.: Высшая школа, 1990.
7. Апатенок Р.Ф., Маркина А.М., Хейман В.Б. Сборник задач по линейной алгебре и аналитической геометрии.  Минск: Высшая школа, 1990.
Минск: Высшая школа, 1990.
8. Галусарьян Р.Т. Введение в математический анализ.  Обнинск: ИАТЭ, 2002.
Обнинск: ИАТЭ, 2002.
9. Галусарьян Р.Т. Методические рекомендации и варианты контрольных работ по математическому анализу.  Обнинск: ИАТЭ, 1998.
Обнинск: ИАТЭ, 1998.
Редактор О.Ю. Волошенко
Компьютерная верстка Р.Т.Галусарьян
ЛР № 020713 от 27.04.98
Подписано к печати Формат бумаги 60х84/16
Печать ризограф, Бумага KYMLUX Печ. л 5
Заказ N Тираж 50 экз. Цена договорная
Отдел множительной техники ИАТЭ, 249040, г. Обнинск, Студгородок,1
