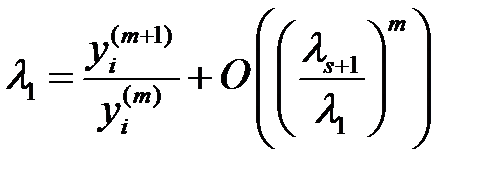Зейдель әдісінің жинақтылыққа жеткілікті шарттары

Айталық 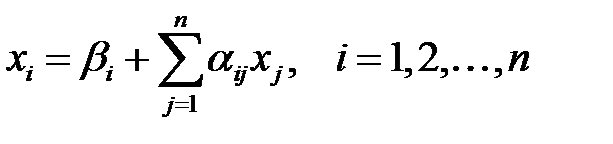жүйесі берілсін. Кез-келген 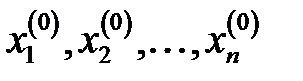жуықтауларын алдық дейік. Енді түбірлерінің 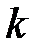-шы жуықтаулары 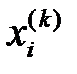белгілі деп түбірлерінің 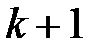-ші жуықтауларын келесі формуласымен есептейміз

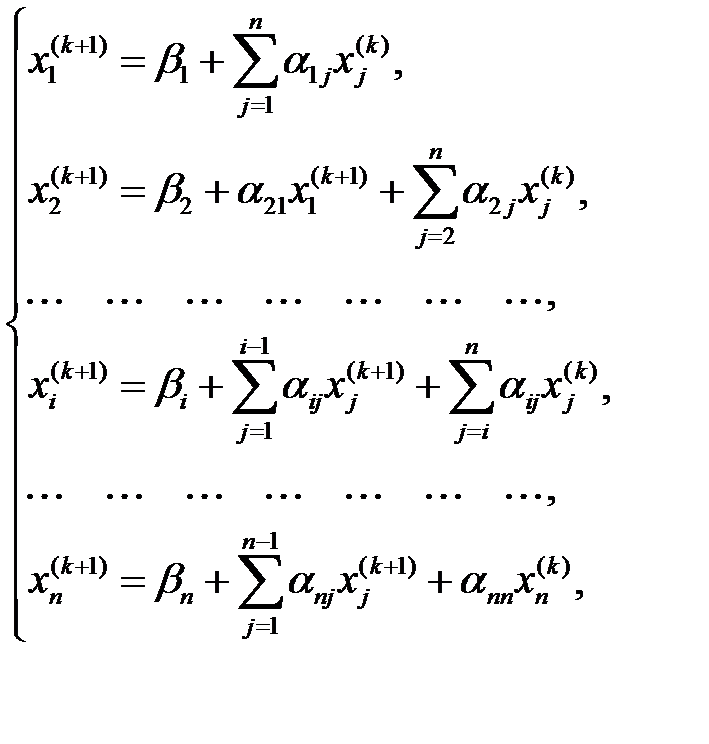
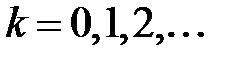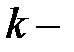, итерация нөмірі.

Зейдель әдісі, қарапайым итерация әдісіне қарағанда, жақсы (тез) жинақтылықты береді. Бірақ-та өте көп есептеулерді қажет етеді. Қарапайым итерация әдісі жинақталмаған жағдайларда да Зейдель әдісі жинақталуы мүмкін. Зейдель әдісінің қарапайым итерация әдісінен жайырақ жинақталатын кездері де болады. Тіпті, қарапайым итерация әдісі жинақталып, Зейдель әдісі жинақталмайтын жағдайлар да болады.

Зейдель процесі жинақталуының жеткілікті шарттары

Теорема 1. Егер

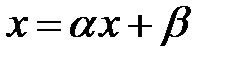(1)

сызықты жүйе үшін

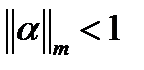(2)

шарты орындалса, мұндағы 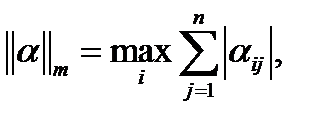онда (1) жүйені шешудің Зейдель процесі осы жүйенің жалғыз шешіміне, кез-келген бастапқы 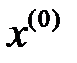векторымен, жинақталады.

Минималды үйлесімсіздіктер әдісі және оның қателігі

Егер біз әрбір 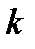итерацияда 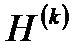түрін 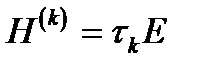түрде іздейтін болсақ, онда минималды үйлесімсіздіктер әдісіне келеміз:

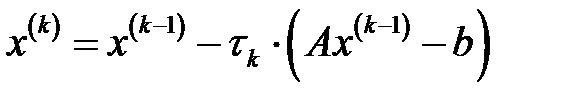, (6)

мұндағы 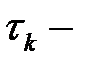параметр. Онда 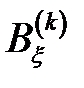және 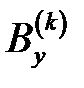бір-бірімен сәйкес келеді де, 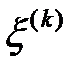үйлесімсіздік векторы үшін 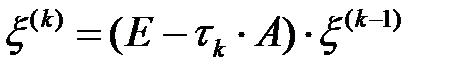қатынасын аламыз.

Келесі белгілеулерін енгізейік 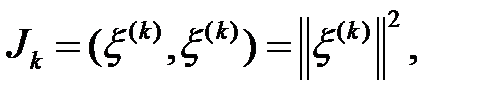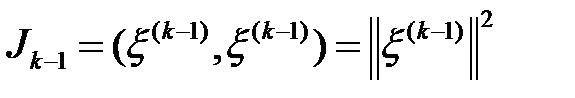. Есептейміз:

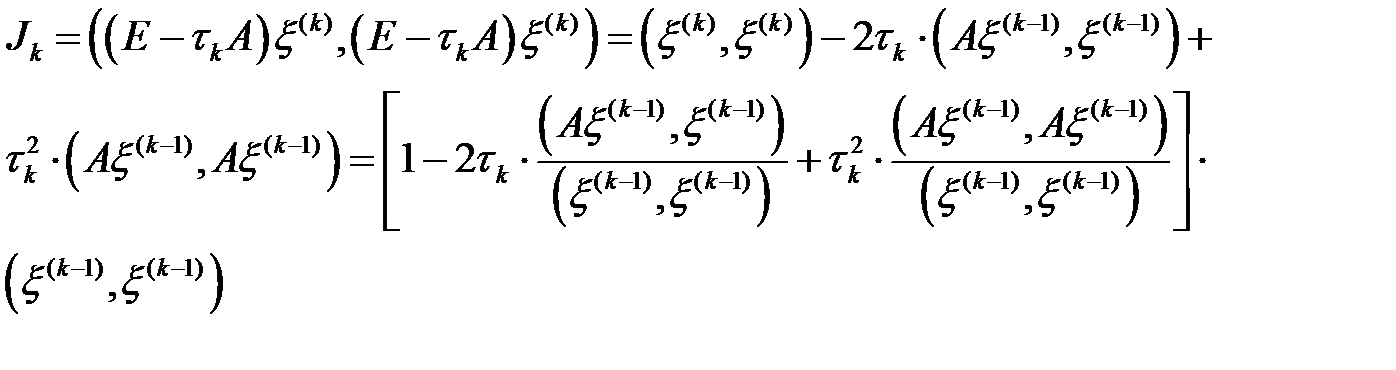
немесе 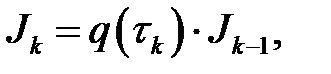мұндағы

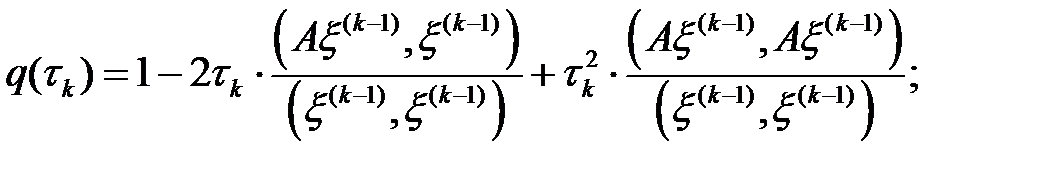
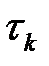параметрін 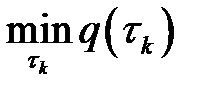шартынан таңдаймыз. Экстремумның қажетті шартынан 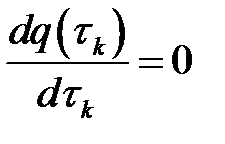шығатыны

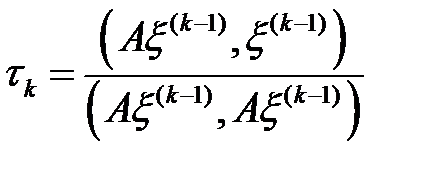. (7)

(7) стационар нүктесінде келесі теңсіздікті тексеру қиын емес 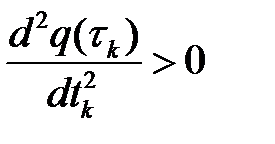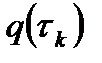функциясы өзінің минимумына жетеді және

.

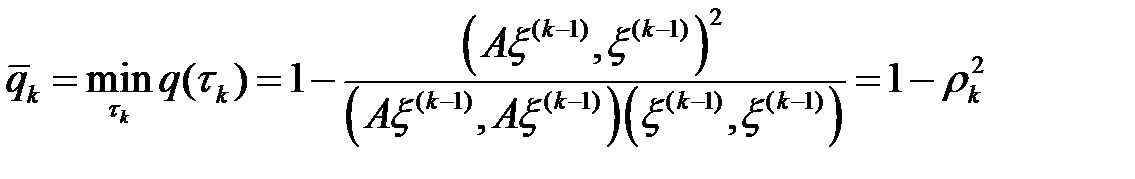Енді 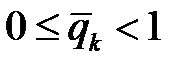теңсіздігі орындалатынын көрсетейік. Коши-Буняковский теңсіздігінен және 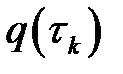өрнегінің теріс еместігінен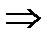 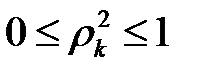. 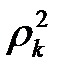нольге ұмтыла алмайды, бірақ төменнен шектелген. Бұл төмендегі тұжырымдардан шығады:

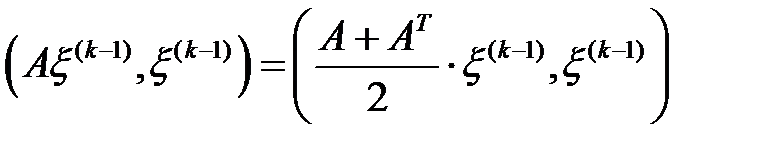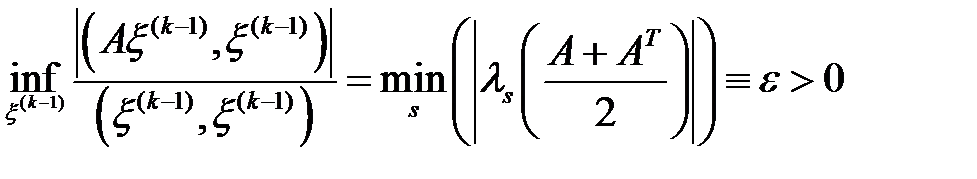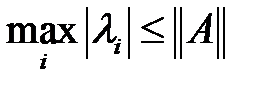
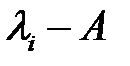, , -ның меншікті мәндері. Бұдан 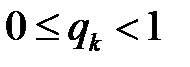теңсіздігінің орындалатыны дәлелденді, себебі 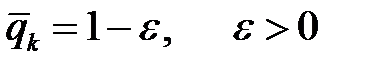. Сонымен, 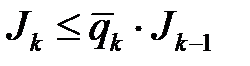немесе 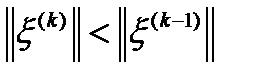, яғни

(6) итерациялық процесс жинақталады!

8. Меншікті мән және меншікті векторларды интерполяциялық әдістерінің алгоритмдерін құру. Ньютон және Ньтон Конторович әдістері

Айталық 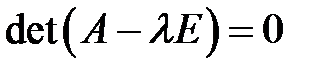теңдеуі берілсін. Бұл теңдеудің түбірлері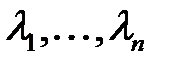 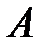матрицасының меншікті мәнідері болсын. Оған сәйкес меншікті векторлары 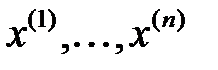болсын. Мұнда 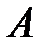нақты матрица, 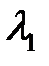нақты сан.

Итерация әдісі.

1-ші жағдай. Айталық 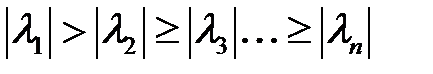болсын. Кез келген 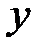векторын аламыз да оны оны 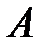матрицасының меншікті векторы 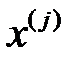бойынша жіктейміз: 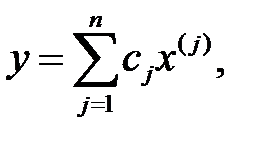(1)

мұндағы 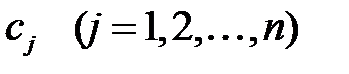тұрақты коэффициенттер.

(1)-ден 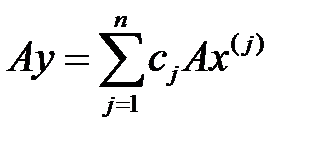(2) шығады ((1)-дің екі жағын да 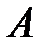матрицасына көбейттік). Енді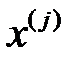 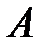түрлендіруінің (матрицасының) меншікті векторы болғандықтан, яғни 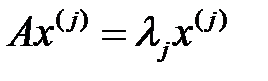орындалғандықтан, (2)-ден алатынымыз

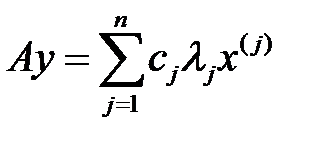. (3)

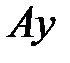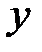– векторының итерациясы. Енді келесі итерацияларын құрамыз: 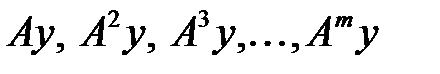, 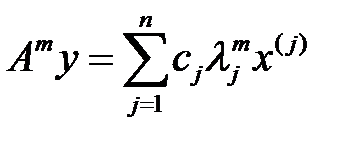. (4)

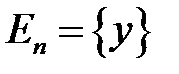кеңістігінде 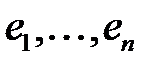базисін таңдап аламыз (бірлік базис болуы міндетті емес).

Айталық, 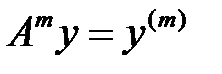, 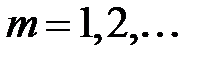дейік. 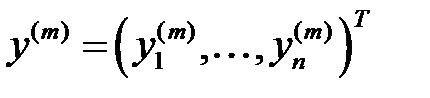, мұндағы 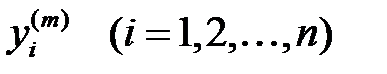– таңдап алынған базистағы вектордың координаттары. 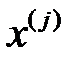меншікті векторын базис векторлары бойынша жіктеп, келесі өрнекті аламыз: 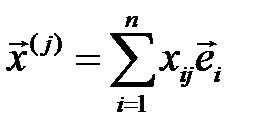. (5)

(5) ті (4) ке қойып, алатынымыз 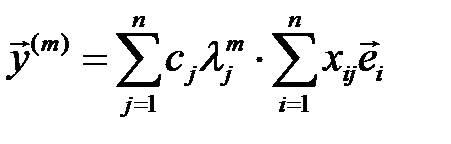(6)

немесе қосындының ретін өзгерте отырып 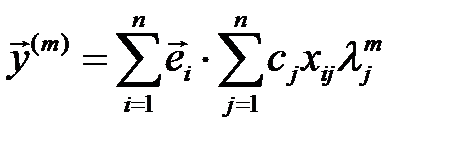. (7)

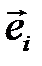векторының коэффициенті 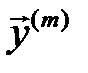векторының 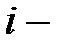ші координатасы болады. Бұдан шығатыны 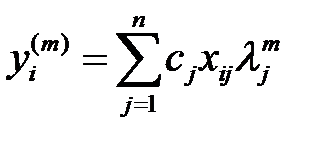. (8)

Сол сияқты 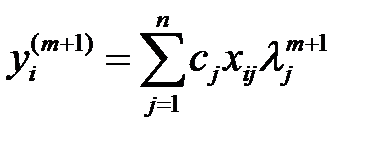. (9)

(8) бен (9) дан

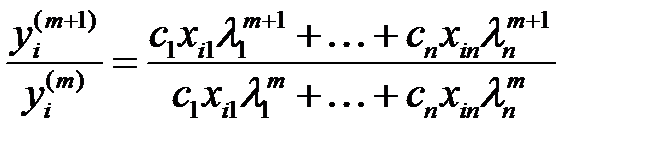. (10)

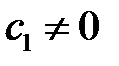және 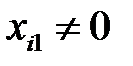деп ұйғарайық. Осылай ұйғаруға әбден болады, себебі 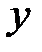векторы мен 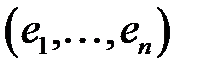базисін таңдау арқылы ұйғарымның дұрыстығына көз жеткіземіз. Онда (10)-нан шығатыны

.

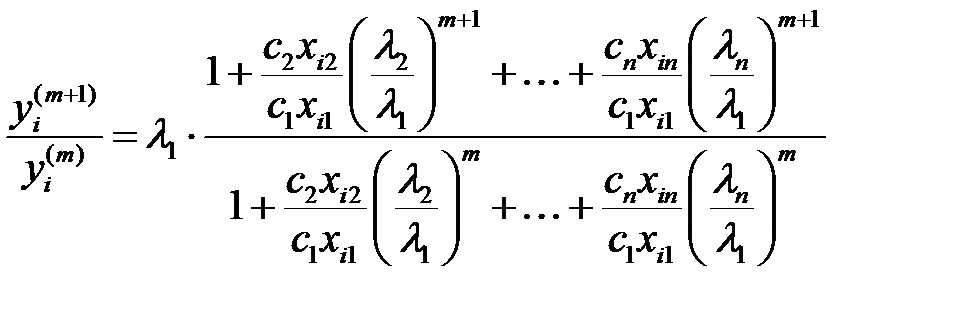Бұдан, 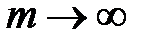десек, онда, 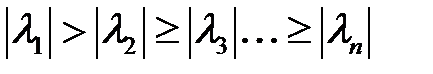орындалатынын ескере отырып, алатынымыз 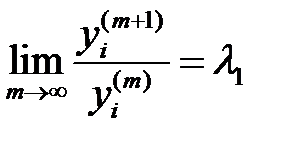. (11)

Ал, 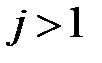кездерде 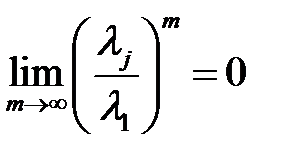болғандықтан, біз жуықтап 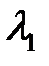-ді табамыз 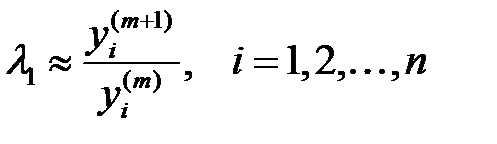. (12)

Дәләрек, .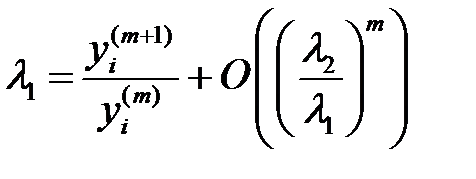

2-ші жағдай. 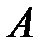матрицасының модулі бойынша ең үлкен меншікті мәні еселі болсын, яғни 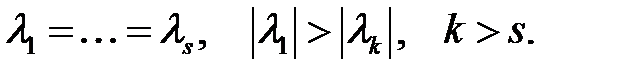Онда алатынымыз

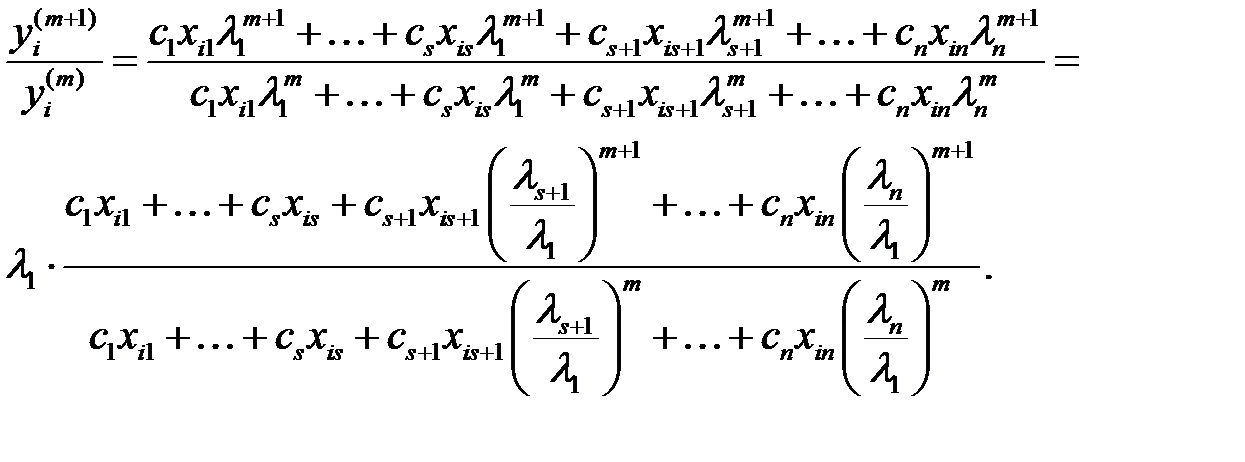
Осыдан, егер 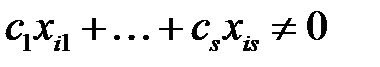боласа және 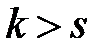болғанда 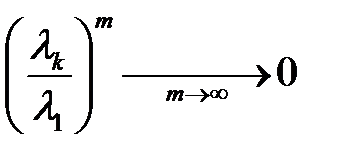болатынын ескерсек, алатынымыз 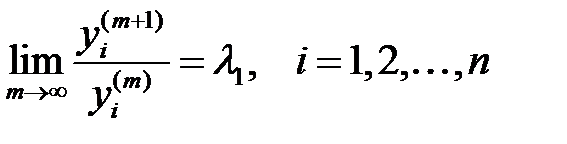. Дәлірек