Бросают игральных костей. Найти метематическое ожидание числа таких бросаний, в каждом из которых выпадет ровно шестерок, если общее число бросаний равно . 4 страница
б) вероятность того, что шары с номерами 1, 4, 5 выпадут в произвольной последовательности равна произведению вероятностей событий А, В, С и количества возможных последовательностей, которые могут составить номера шаров :
Р = 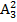
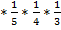 =
= 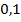
№69 Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.
Решение:
Введём обозначения событий: А – студент знает ответ на первый вопрос, В – студент знает ответ на второй вопрос, С – студент знает ответ на третий вопрос. Вероятность события А равна отношению количества вопросов которые знает студент, к общему количеству вопросов: Р(А) = 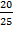 =
=  . Вероятность события В при условии А -
. Вероятность события В при условии А - 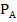 (В) =
(В) = 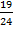 , вероятность С при условии А, В -
, вероятность С при условии А, В - 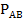 (С) =
(С) = 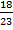 . Вероятность того, что студент знает все три вопроса по правилу умножения вероятностей равна : Р =
. Вероятность того, что студент знает все три вопроса по правилу умножения вероятностей равна : Р = 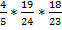 =
= 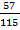 ≈ 0, 23.
≈ 0, 23.
№70 В мешочке содержится 10 одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному три кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3 , если кубики извлекаются: а) без возврата; б) с возвратом (извлеченный кубик возвращается в мешочек).
Решение:
a) введем обозначение событий: А – выпал кубик с номером 1, В – выпал кубик с номером 2, С – выпал кубик с номером 3. Вероятность наступления события А – Р(А) =  . Вероятность наступления события В при условии, что событие А уже наступило -
. Вероятность наступления события В при условии, что событие А уже наступило -  (В) =
(В) =  , вероятность события С при условии А, В -
, вероятность события С при условии А, В -  (С) =
(С) = 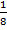 . Искомая вероятность того, что при вынимании без возврата выпадут кубики с номерами 1, 2, 3 по правилу умножения равна произведению вероятностей событий А, В, С : Р =
. Искомая вероятность того, что при вынимании без возврата выпадут кубики с номерами 1, 2, 3 по правилу умножения равна произведению вероятностей событий А, В, С : Р = 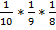 =
= 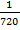 .
.
б) вероятность того, что выпадут кубики с номерами 1, 2, 3 при вынимании их с возвращением обратно равна произведению равных вероятностей событий А, В, С:
Р = 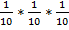 =
= 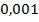 .
.
№71 По данным переписи населения (1981г.) Англии и Уэльса установлено: темноглазые отцы и темноглазые сыновья составили 5% обследованных лиц, темноглазые отцы и светлоглазые сыновья - 7,9%, Светлоглазые отцы и темноглазые сыновья – 8,9%, Светлоглазые отцы и светлоглазые сыновья – 78,2%. Найти связь между цветом глаз отца и сына.
Решение:
По условию, 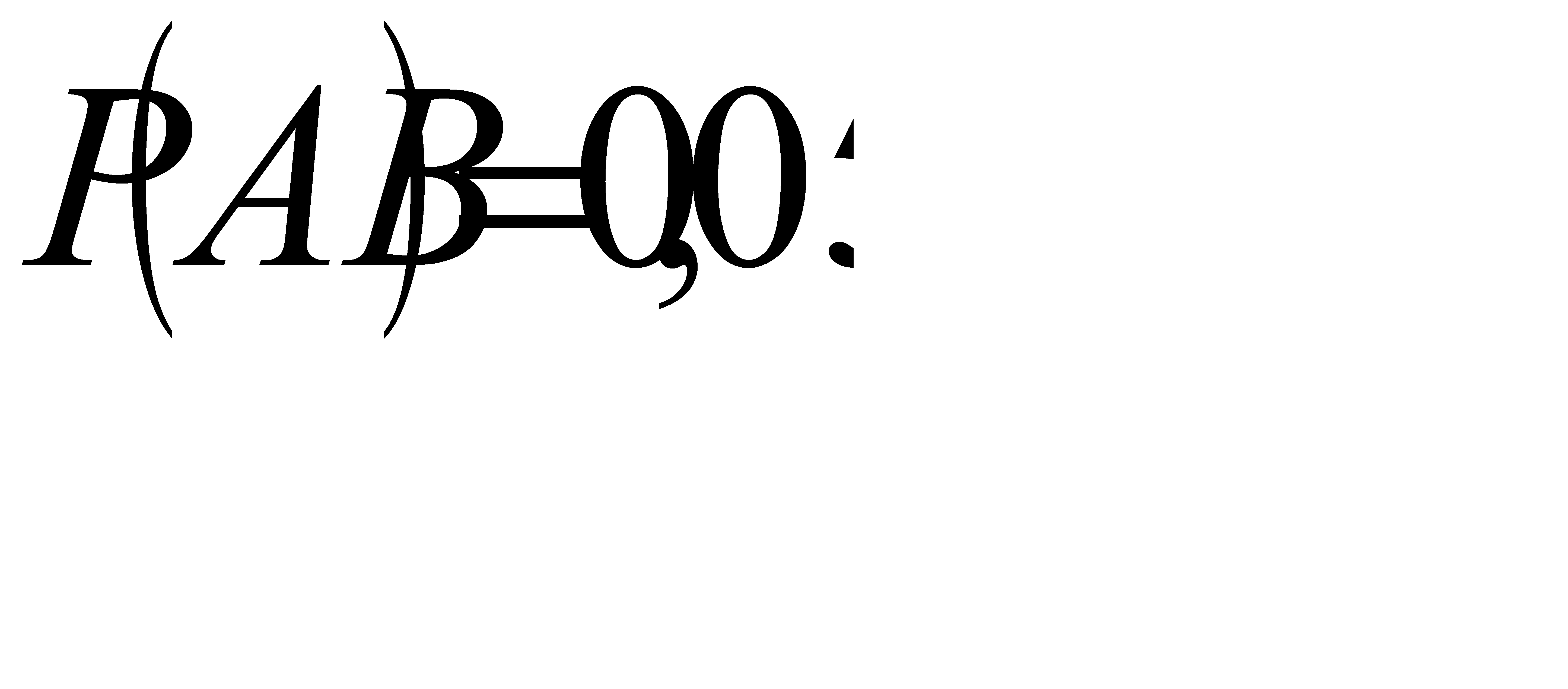
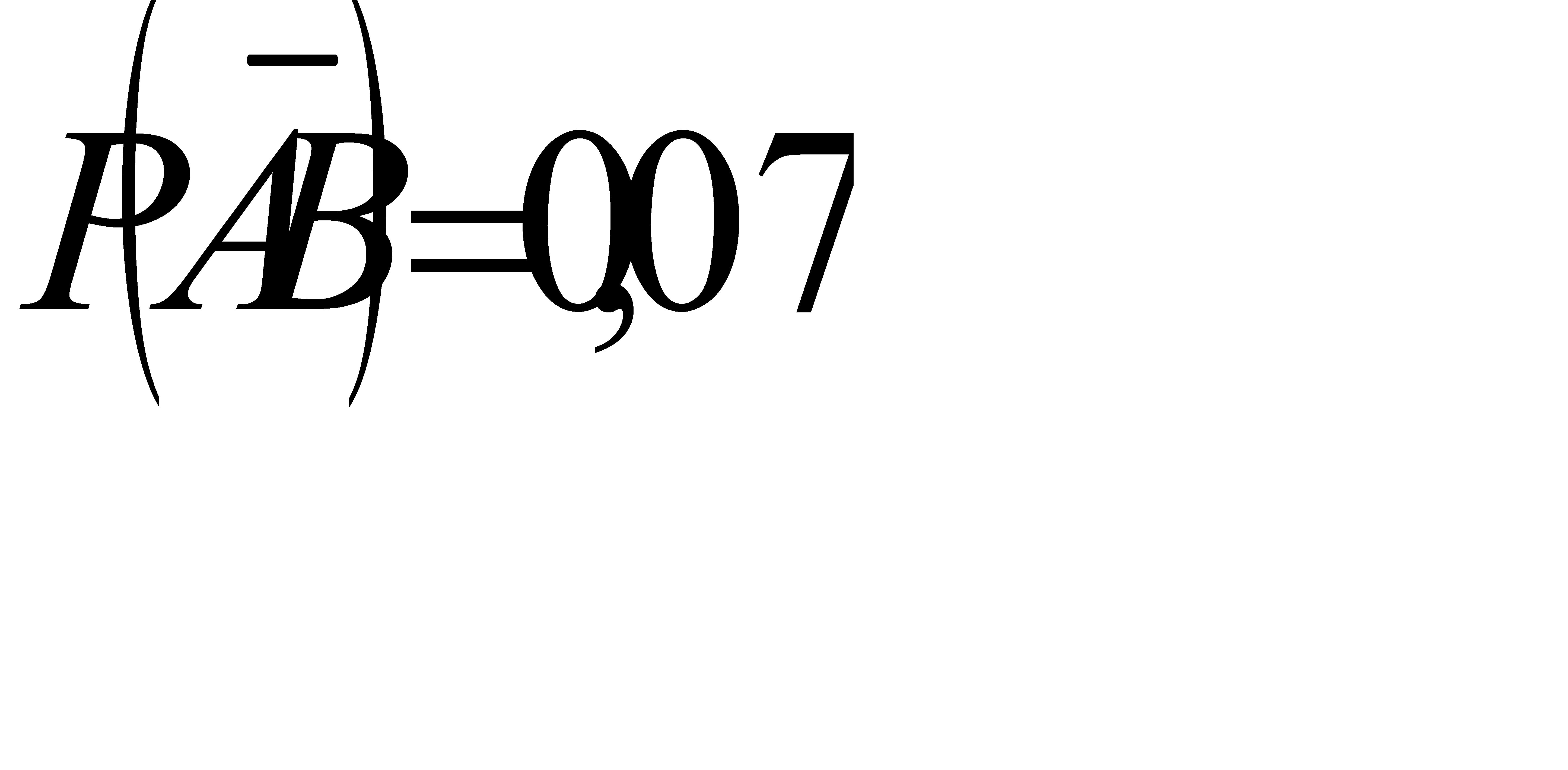
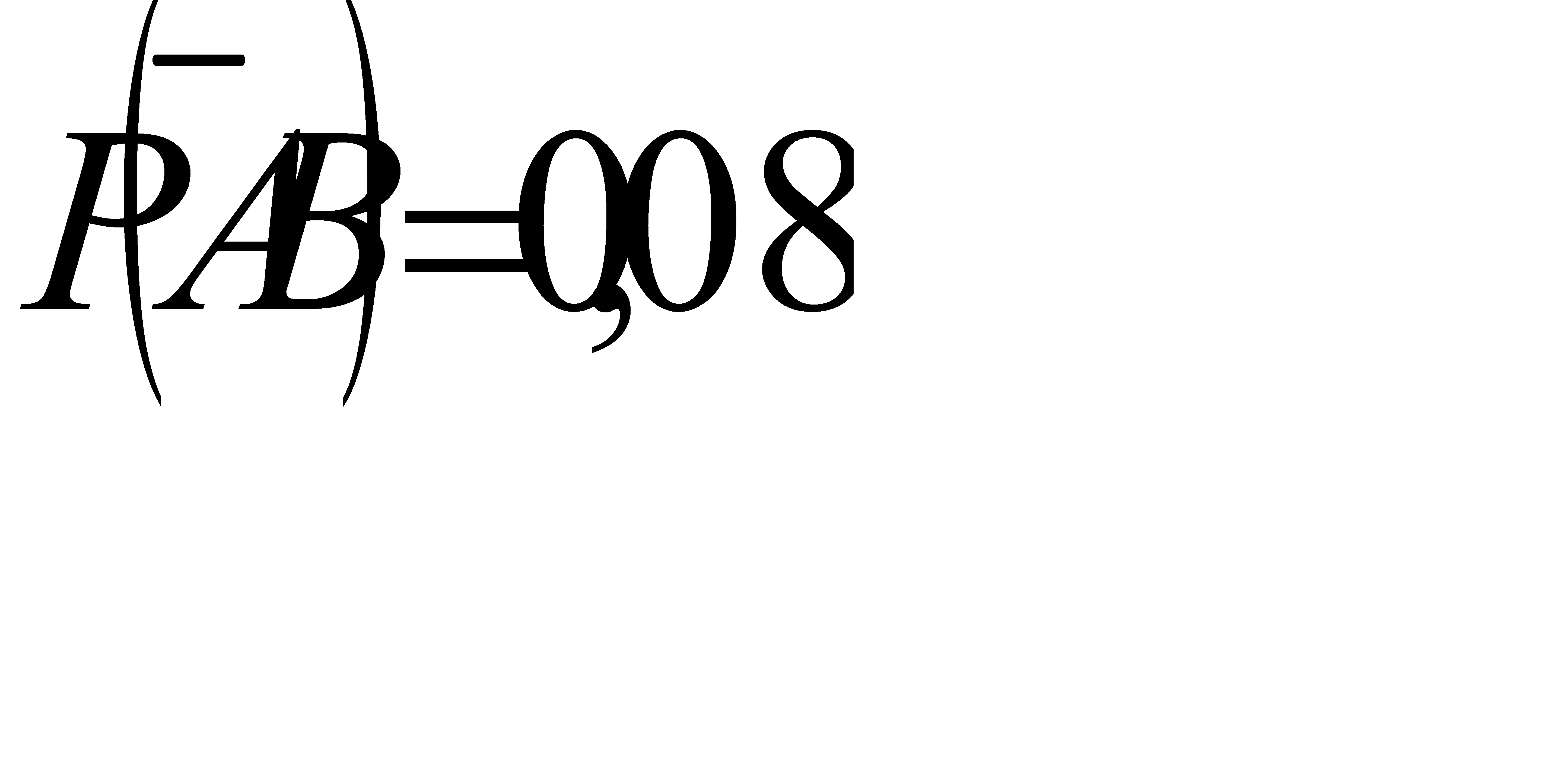

Найдем условную вероятность того, что сын темноглазый если отец темноглазый:

Найдем условную вероятность того, что сын светлоглазый, если отец темноглазый:

Найдем условную вероятность того, что сын темноглазый, если отец светлоглазый:

Найдем условную вероятность того, что сын светлоглазый, если отец светлоглазый:

№72 Найти вероятность Р(А) по данным вероятностям:
Р(АВ)=0,72, Р(А 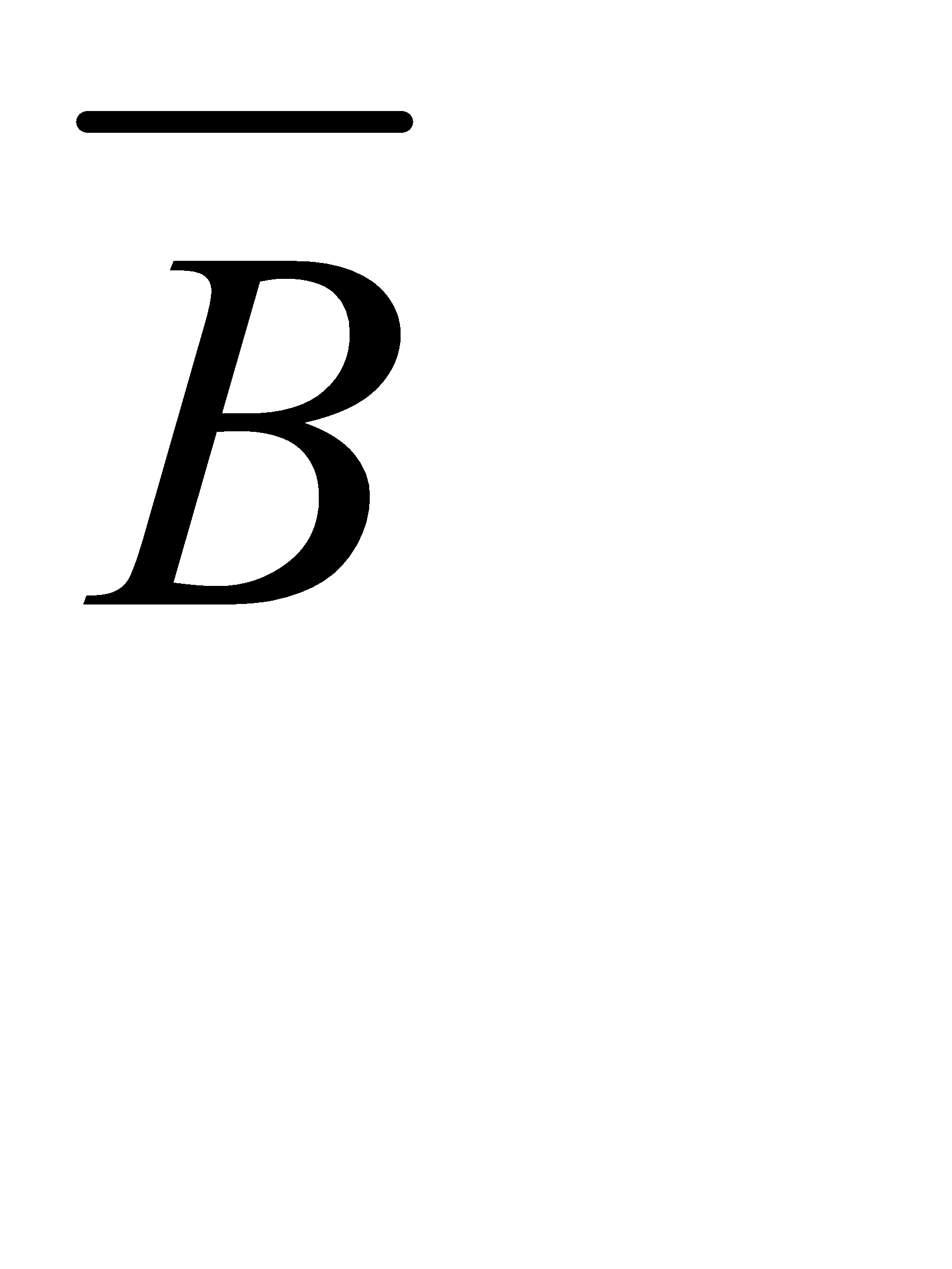 )=0,18.
)=0,18.
Решение.
Событие А можно представить в виде суммы следующих двух несовместных событий:
А=АВ+ А 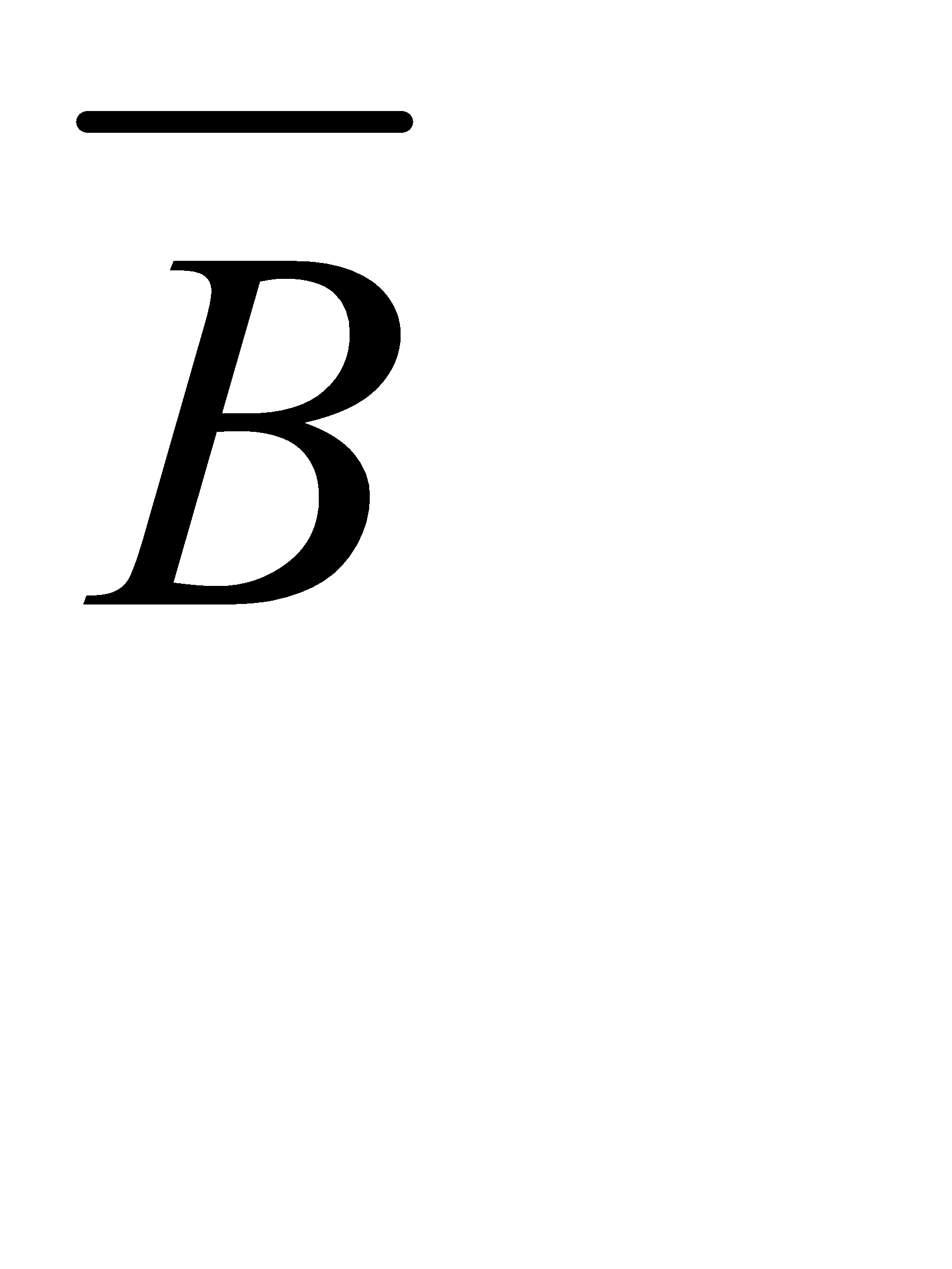 . По теореме сложения вероятностей несовместных событий получим
. По теореме сложения вероятностей несовместных событий получим
Р(А)= Р(АВ+ А 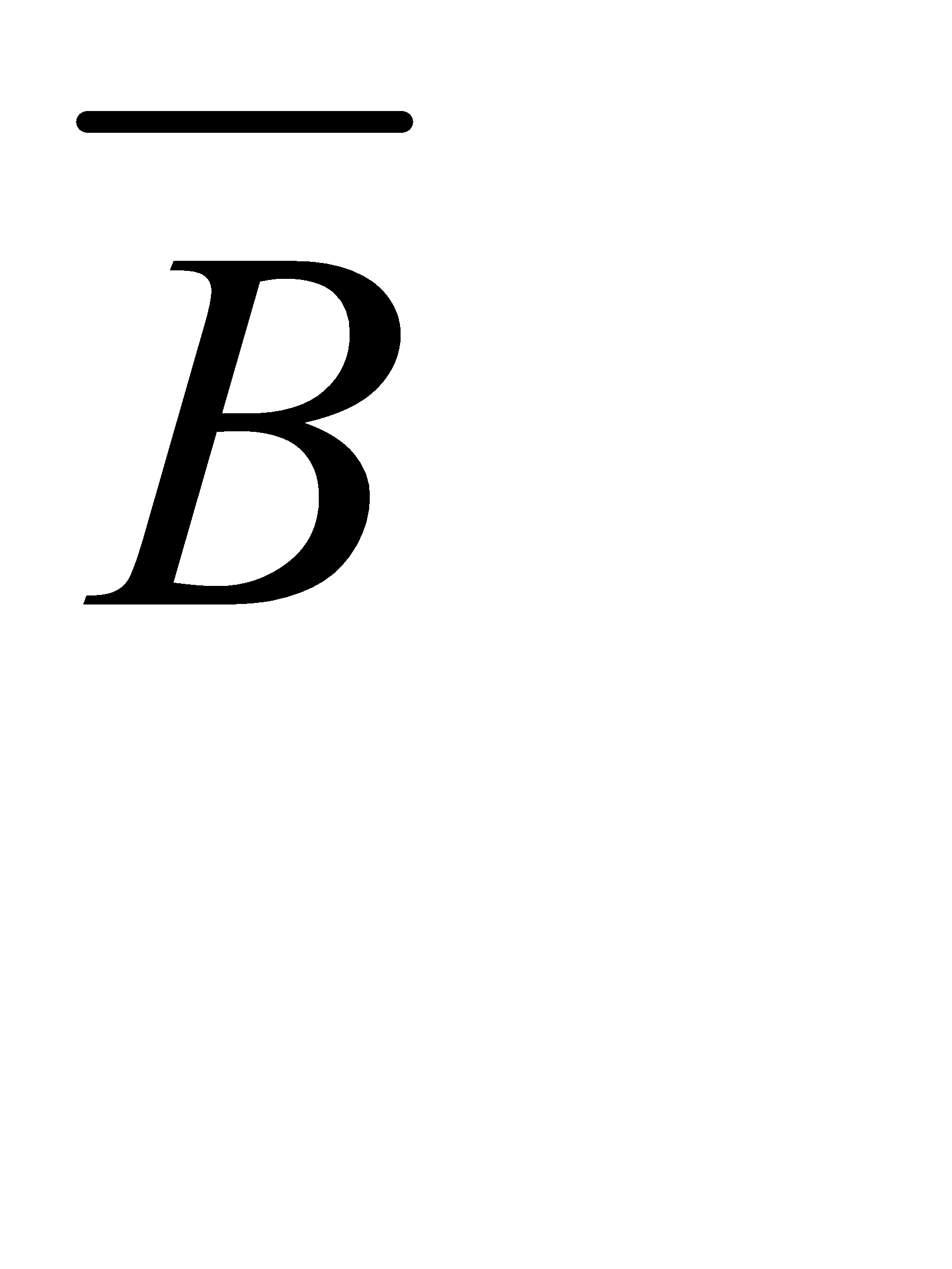 )=Р(АВ)+Р(А
)=Р(АВ)+Р(А 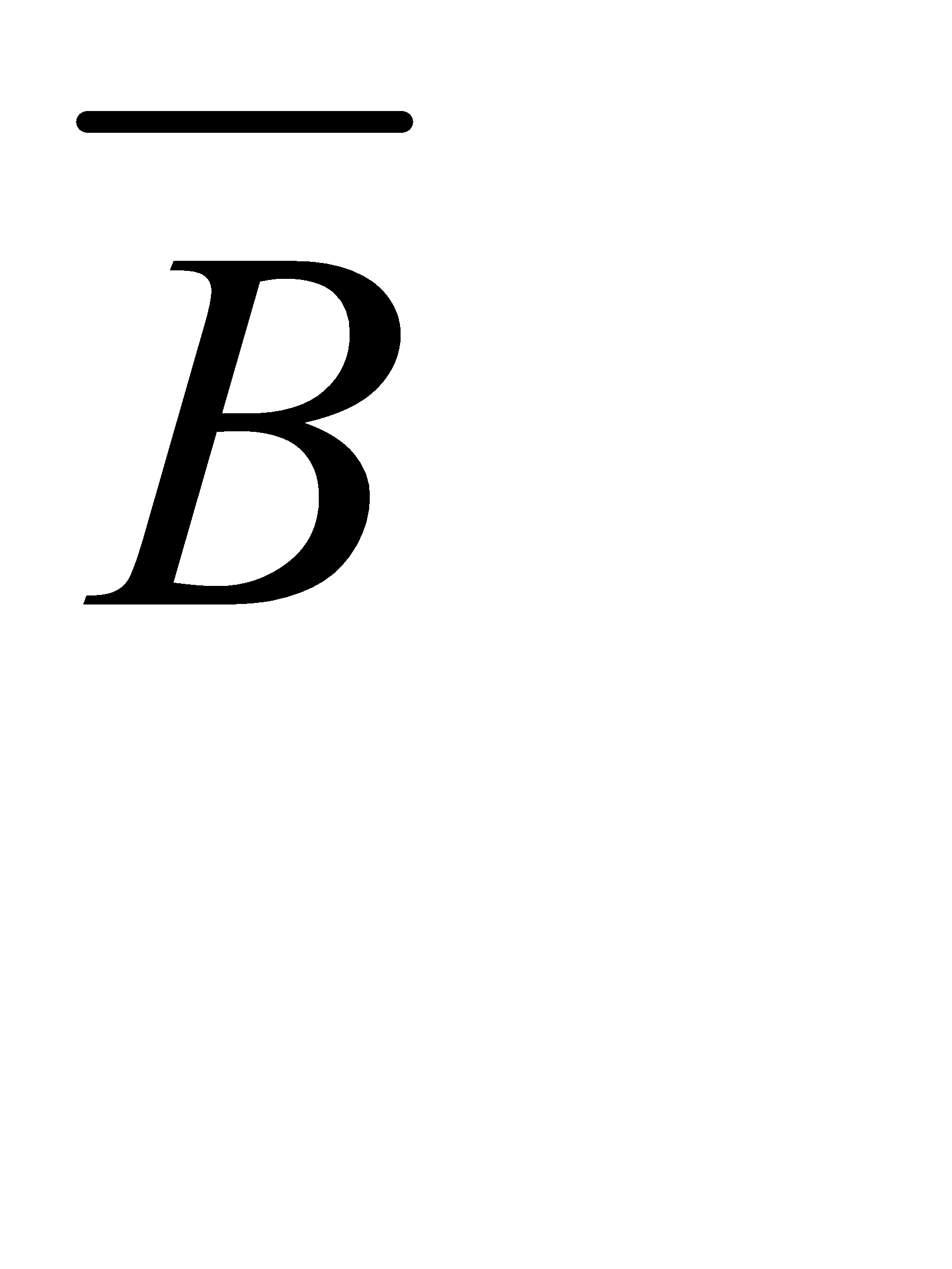 )=0,72+0,18=0,9.
)=0,72+0,18=0,9.
Ответ:0,9
Захаров Сергей
№73 Найти вероятность 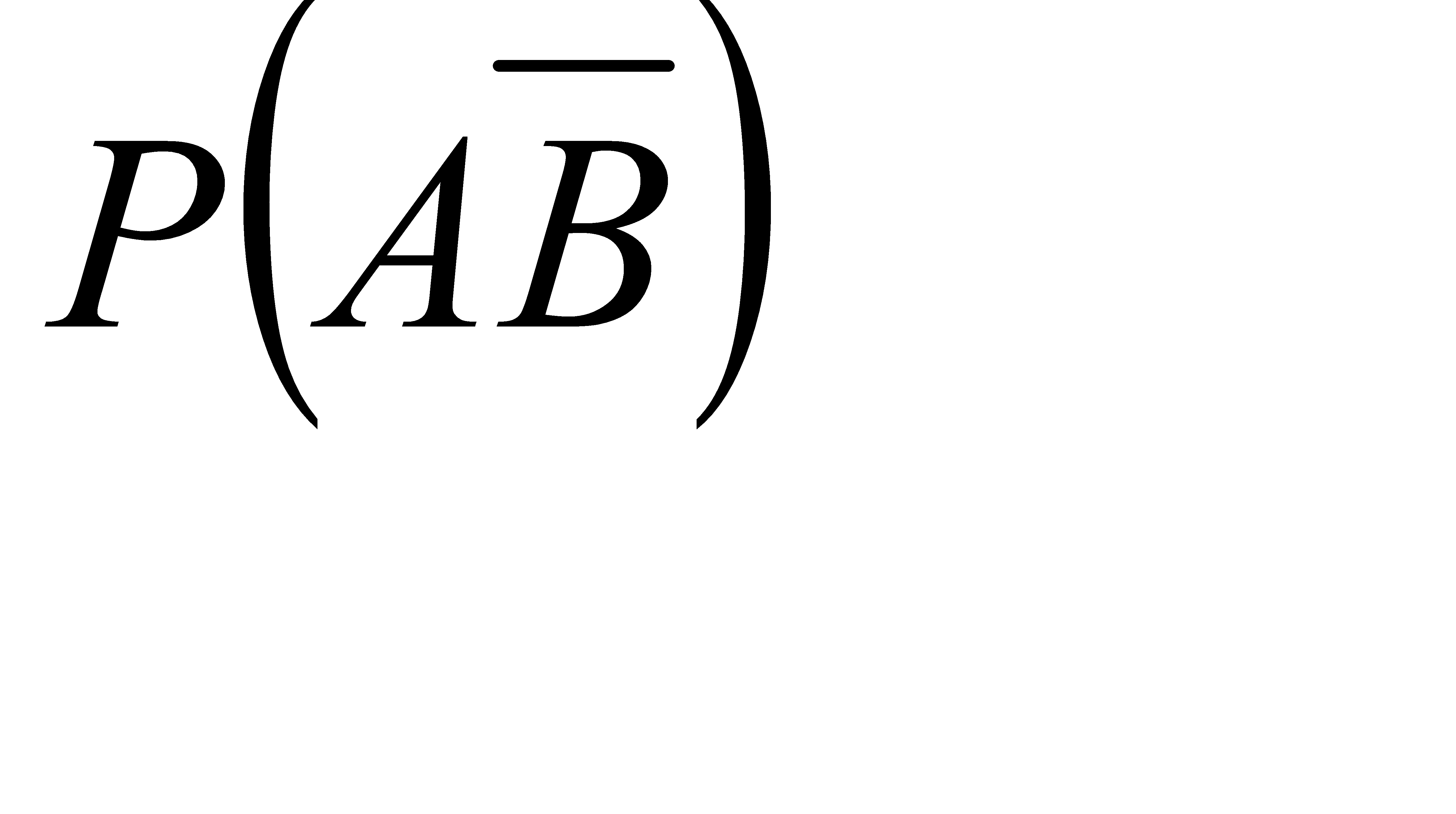 по данным вероятностям:
по данным вероятностям: 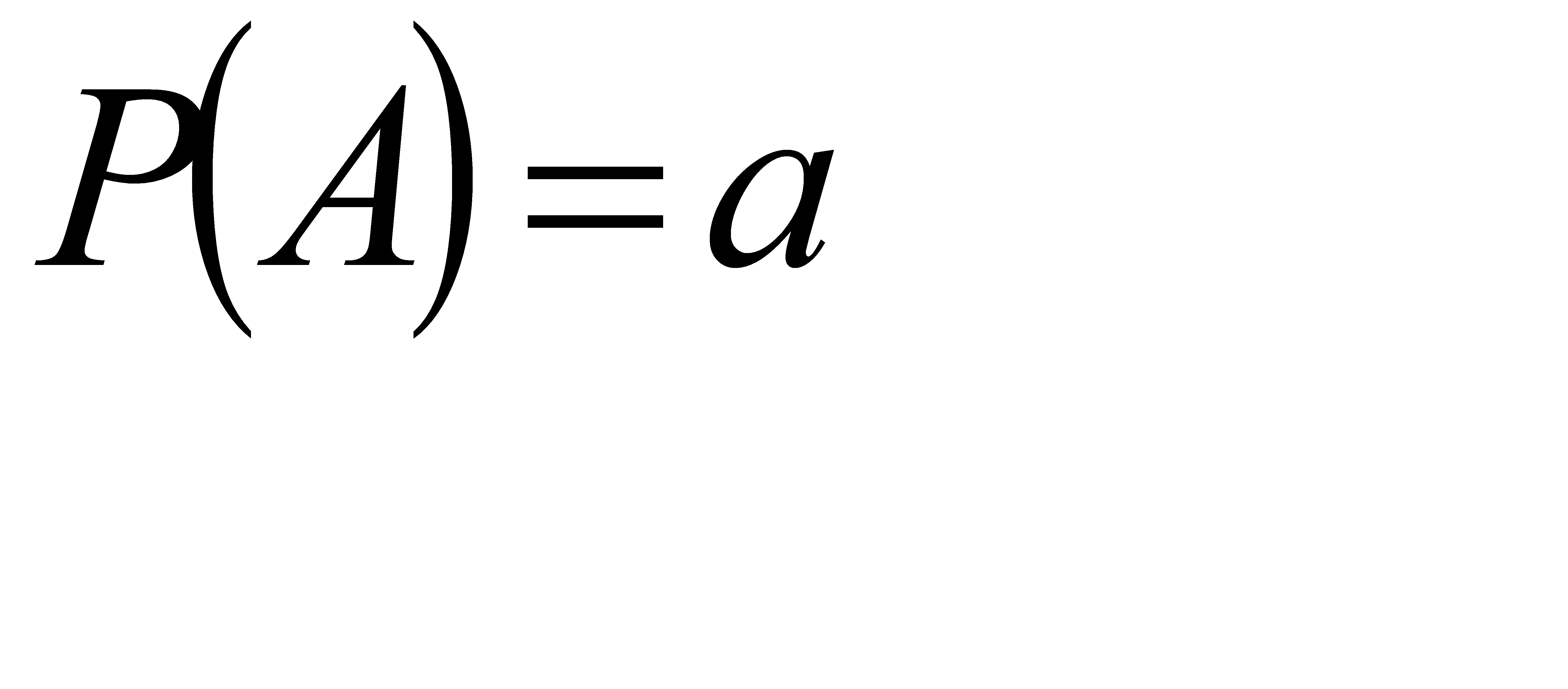 ,
, 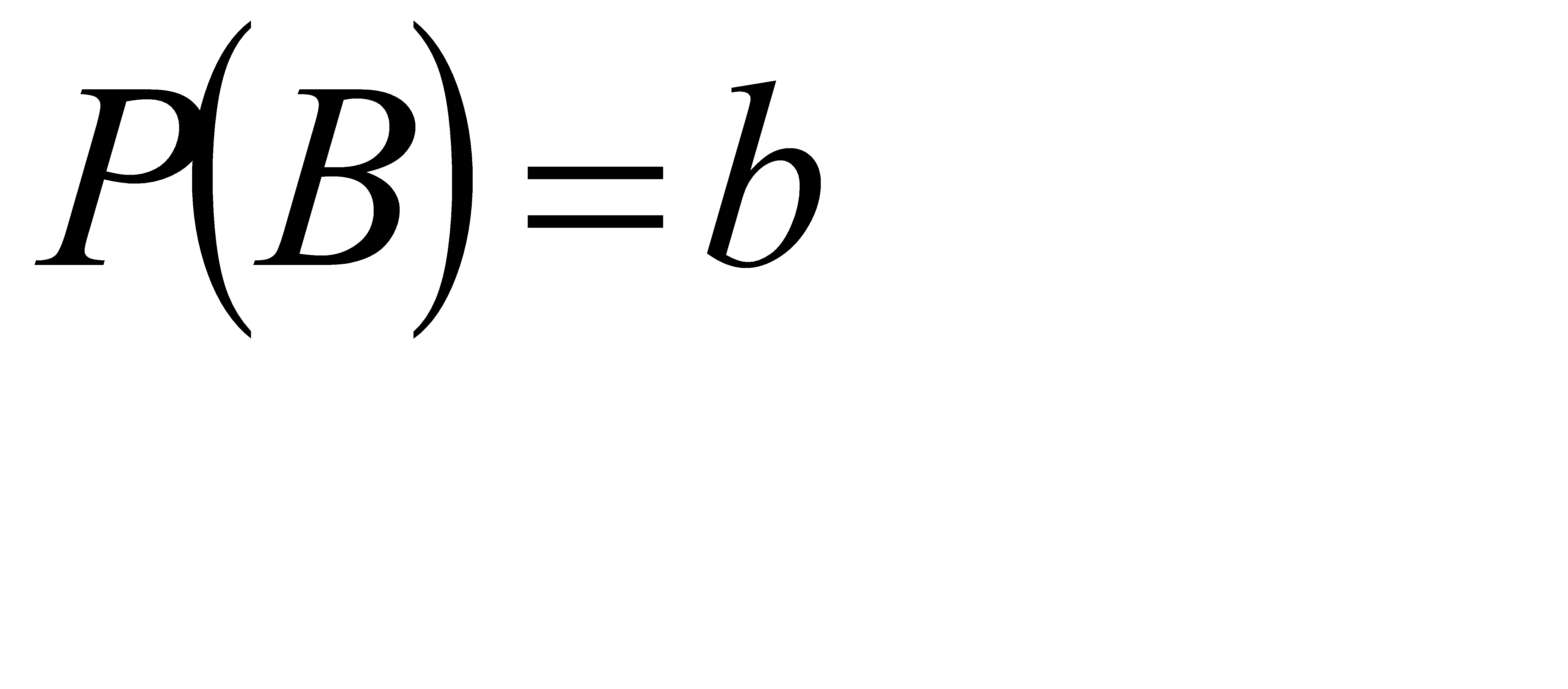 ,
, 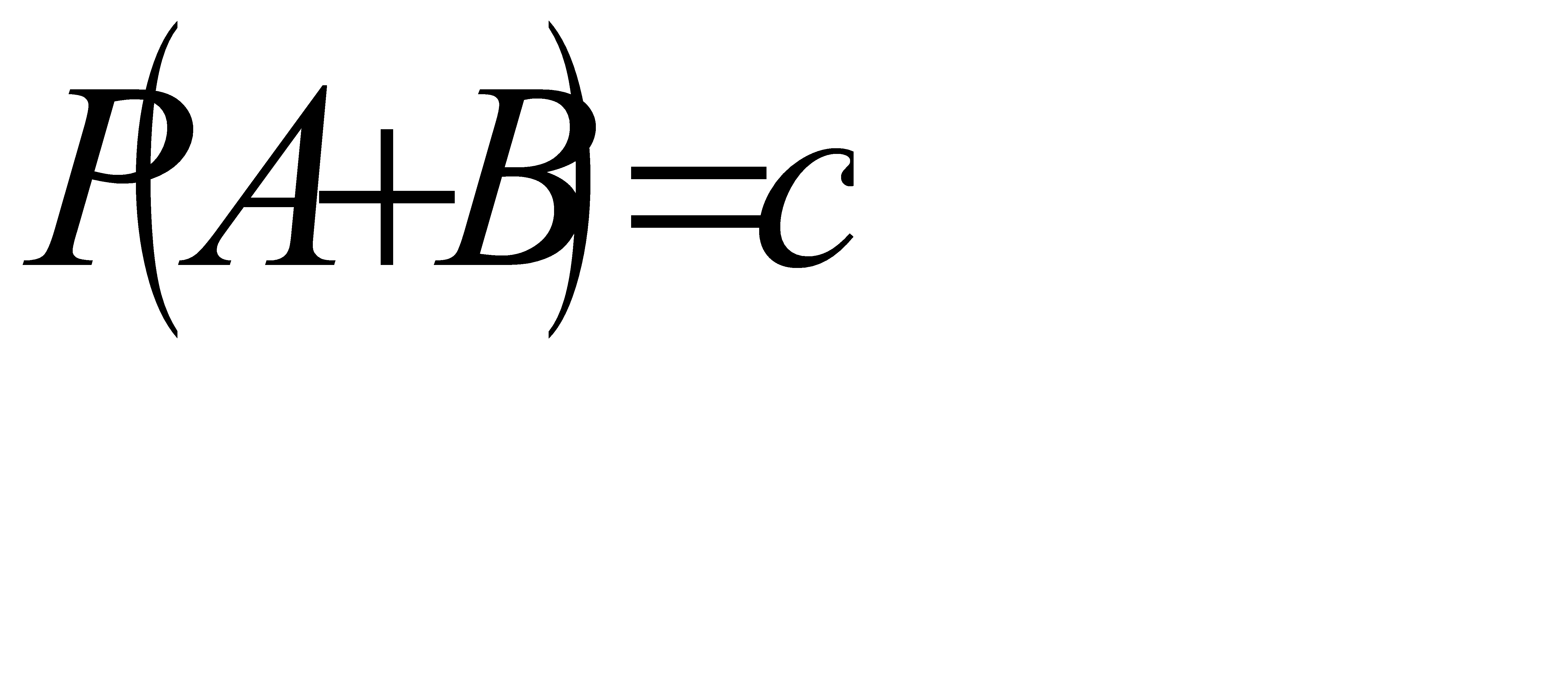 .
.
Решение.
Используя тождество  найдём
найдём
 (*)
(*)
Из равенства  выразим
выразим 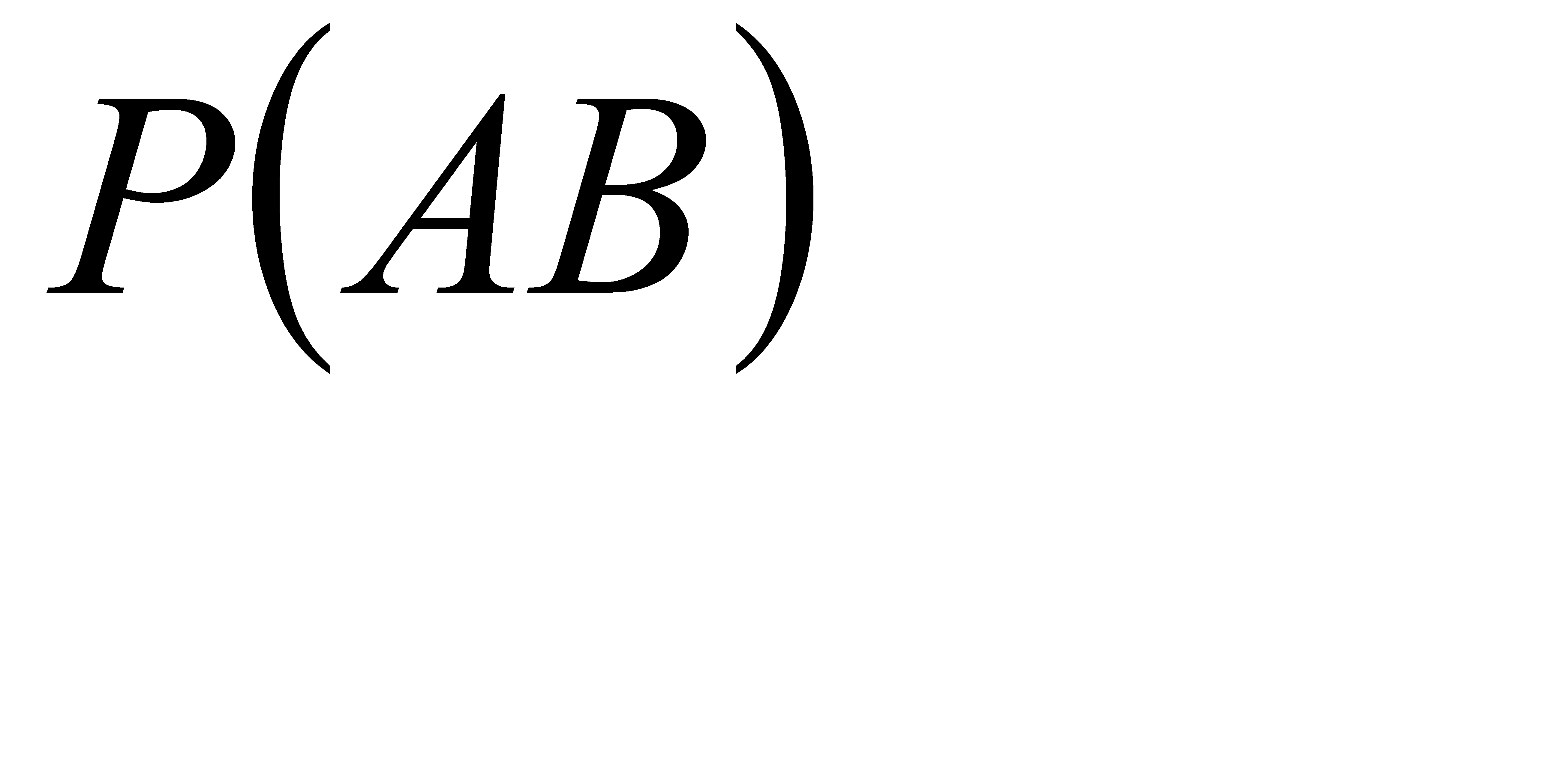 :
:
 (**)
(**)
Подставив (**) в (*), получим

№74 Найти вероятность 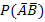 по данным вероятностям:
по данным вероятностям:
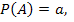
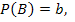
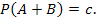
Решение
Используя тождество 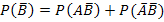 , найдем
, найдем 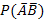 :
:
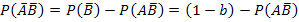
Подставив в последнее равенство 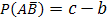 (см. задачу 73), получим:
(см. задачу 73), получим:
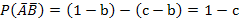 .
.
№73 Наступление события  необходимо влечёт наступление события
необходимо влечёт наступление события  . Доказать, что
. Доказать, что 
Решение:
По условию, наступление события АВ влечёт наступление события  , поэтому.
, поэтому. 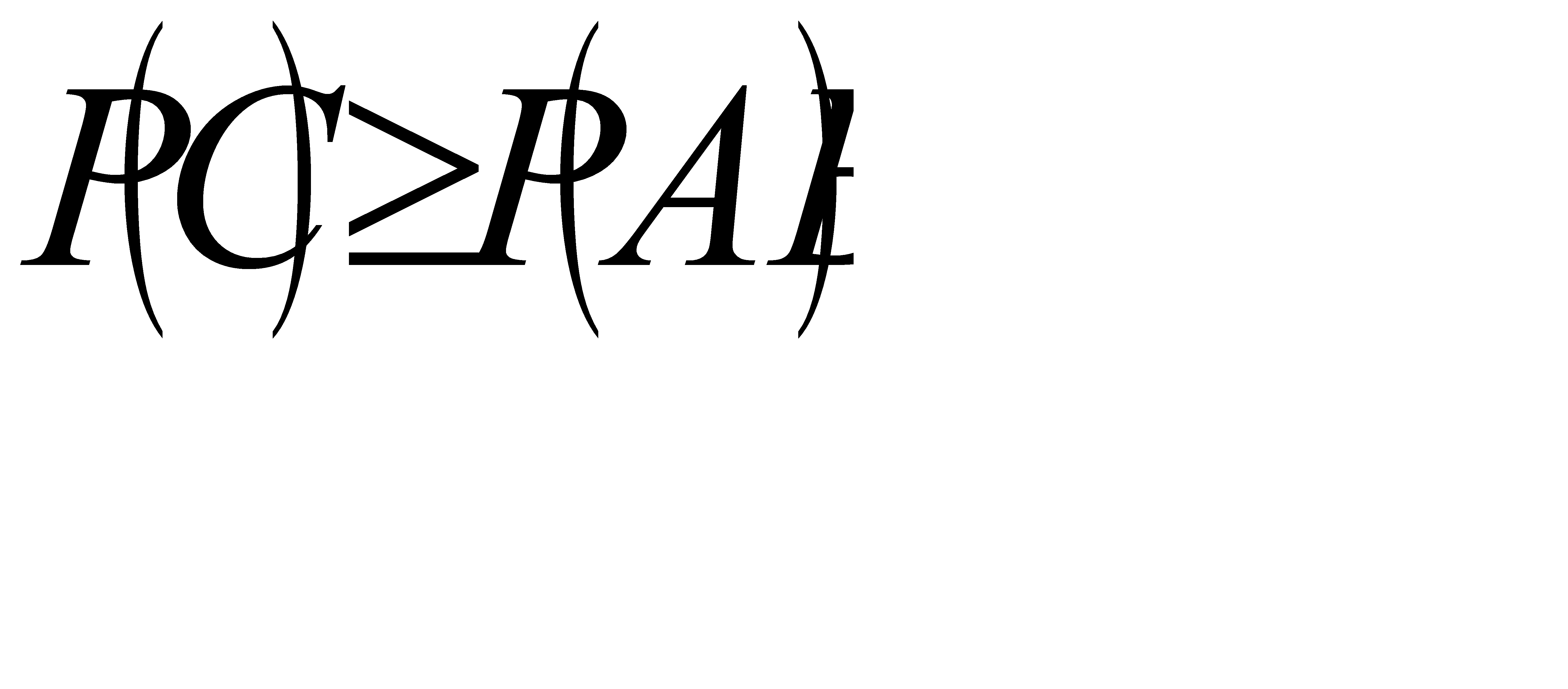 (*)
(*)
Используя тождества  ,
,  ,
, 
и учитывая неравенство (*), получим

№№74-75№№
№76 Доказать, что PA(B)≥1 - P(B)/P(A). Предполагается, что P(A)>0.
Решение.
Справедливо неравенство: P(A) + P(B) - P(AB) ≤1.
Воспользуемся тождествами: P(AB) = P(A)*PA(B), P(B) = 1 – P(B).
Подставив P(AB) = P(A)*PA(B), P(B) = 1 – P(B) в P(A) + P(B) - P(AB) ≤1,
получим P(A) + 1 – P(B) – P(A)*PA(B) ≤1, или
P(A)*PA(B) ≥ P(A) – P(B).
Разделив обе части неравенства на положительное число P(A), окончательно имеем:
PA(B) ≥ 1 - P(B) / P(A)
№77 По условию, наступление события 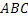 необходимо влечет наступление события
необходимо влечет наступление события 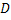 , следовательно (см. задачу 48),
, следовательно (см. задачу 48), 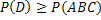 . Таким образом, если будет доказано неравенство
. Таким образом, если будет доказано неравенство 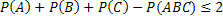 (*), то будет справедливо и неравенство, указанное в условии задачи.
(*), то будет справедливо и неравенство, указанное в условии задачи.
Докажем неравенство (*). Воспользуемся тождествами:
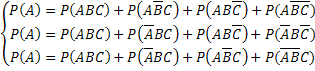 (**)
(**)
Из трех событий 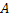 ,
, 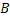 ,
, 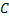 можно составить следующую полную группу «сложных событий», состоящих из появлений и непоявлений рассматриваемых трех событий:
можно составить следующую полную группу «сложных событий», состоящих из появлений и непоявлений рассматриваемых трех событий:
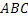 -появились все три события,
-появились все три события,
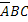 ,
, 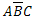 ,
, 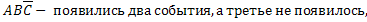
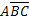 ,
, 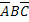 ,
, 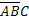 – появилось одно событие, а два других не появились,
– появилось одно событие, а два других не появились,
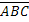 – не появились все три события.
– не появились все три события.
Сумма вероятностей событий, образующих полную группу, равна единице, поэтому
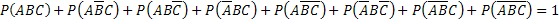
Отсюда
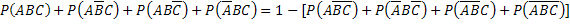 . (***)
. (***)
Подставив (**) в (*) и используя (***), после упрощений получим
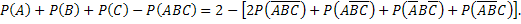
Учитывая, что каждое слагаемое в квадратной скобке неотрицательно, окончательно получим
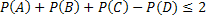 .
.
№78 Вывести теорему сложения вероятностей для трех совместных событий:
P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).
Предполагается, что для двух совместных событий теорема сложения уже доказана:
P(A1 + A2) = P(A1) + P(A2) – P(A1A2).
Решение.
Сведем сумму трех событий к сумме двух событий: А + В + С = (А + В) + С.
Воспользуемся теоремой сложения вероятностей двух событий:
Р(А + В + С) = Р[(А + В) + С] = Р(А + В) + Р(С) - Р[(А + В)*С] = Р(А + В) + Р(С) - Р[(А*С) + (В*С)]
Применим теорему сложения вероятностей двух совместных событий дважды (для событий А и В, а также для событий АС и ВС):
Р(А + В + С) = Р(А) + Р(В) – Р(АВ) + Р(С) - {Р(АС) + Р(ВС) – Р[(АС)(ВС)]}.
Учитывая, что Р[(АС)(ВС)] = Р(АВС), окончательно получим P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).
№79 Даны три попарно независимых события A, B, C, которые, однако, все три вместе произойти не могут. Предполагая, что все они имеют одну и ту же вероятность p, найти наибольшее возможное значение p.
Решение.
Так как события попарно независимы и 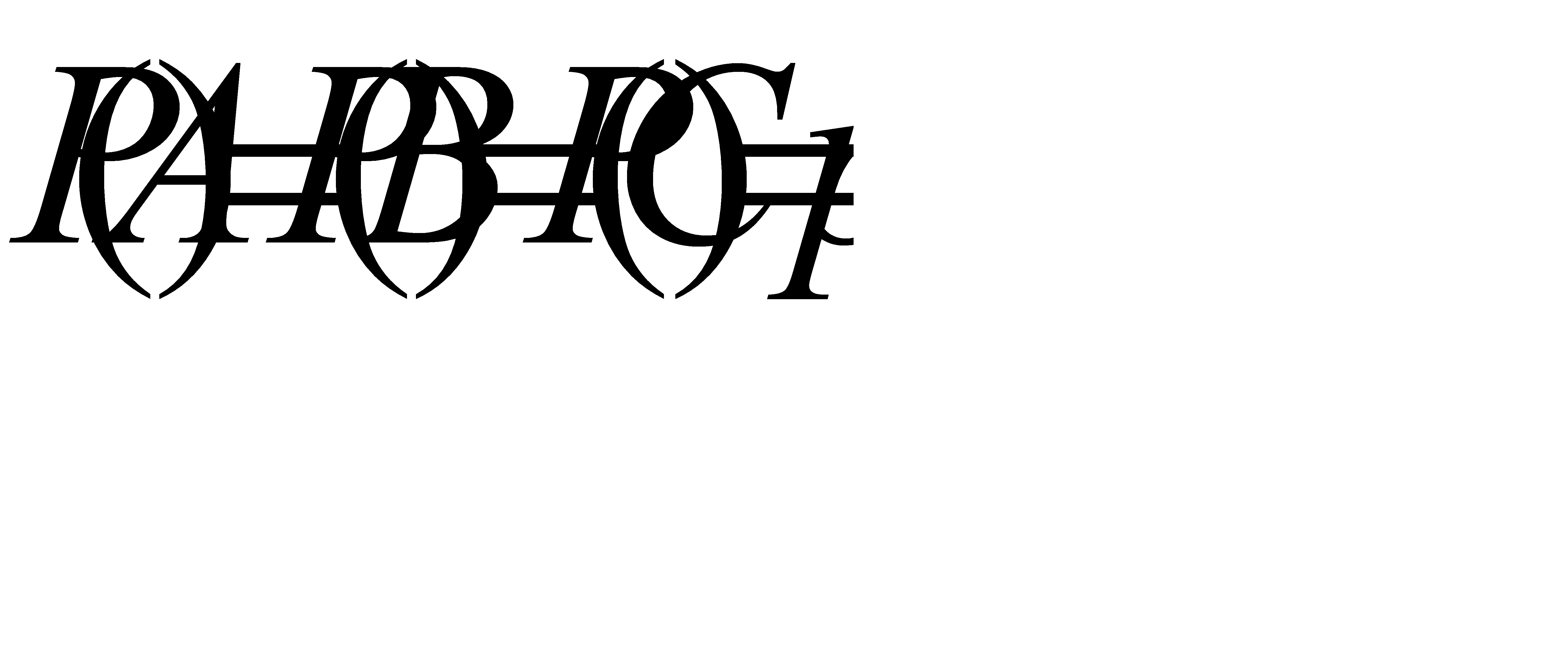 , также верно
, также верно 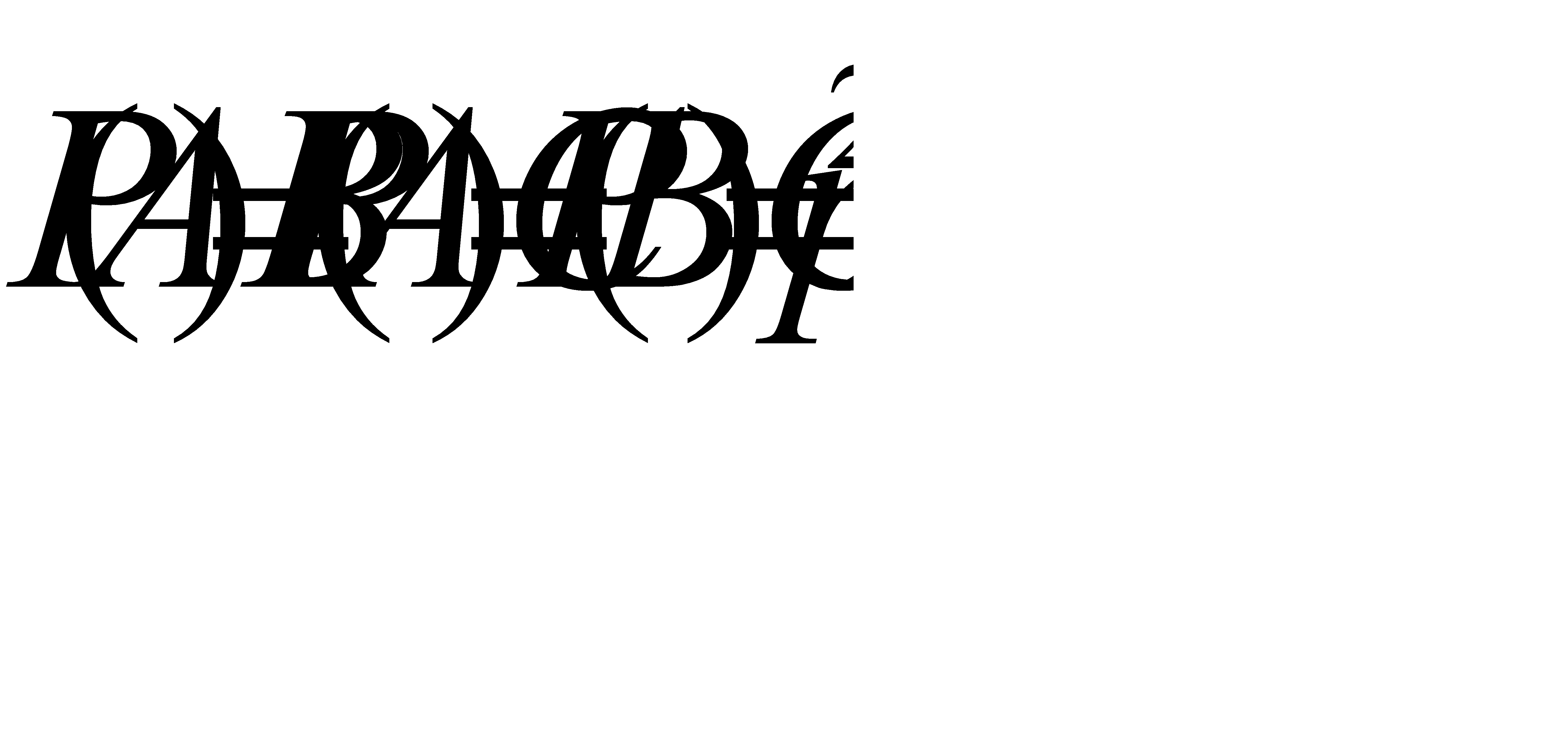 .
.
Обозначим 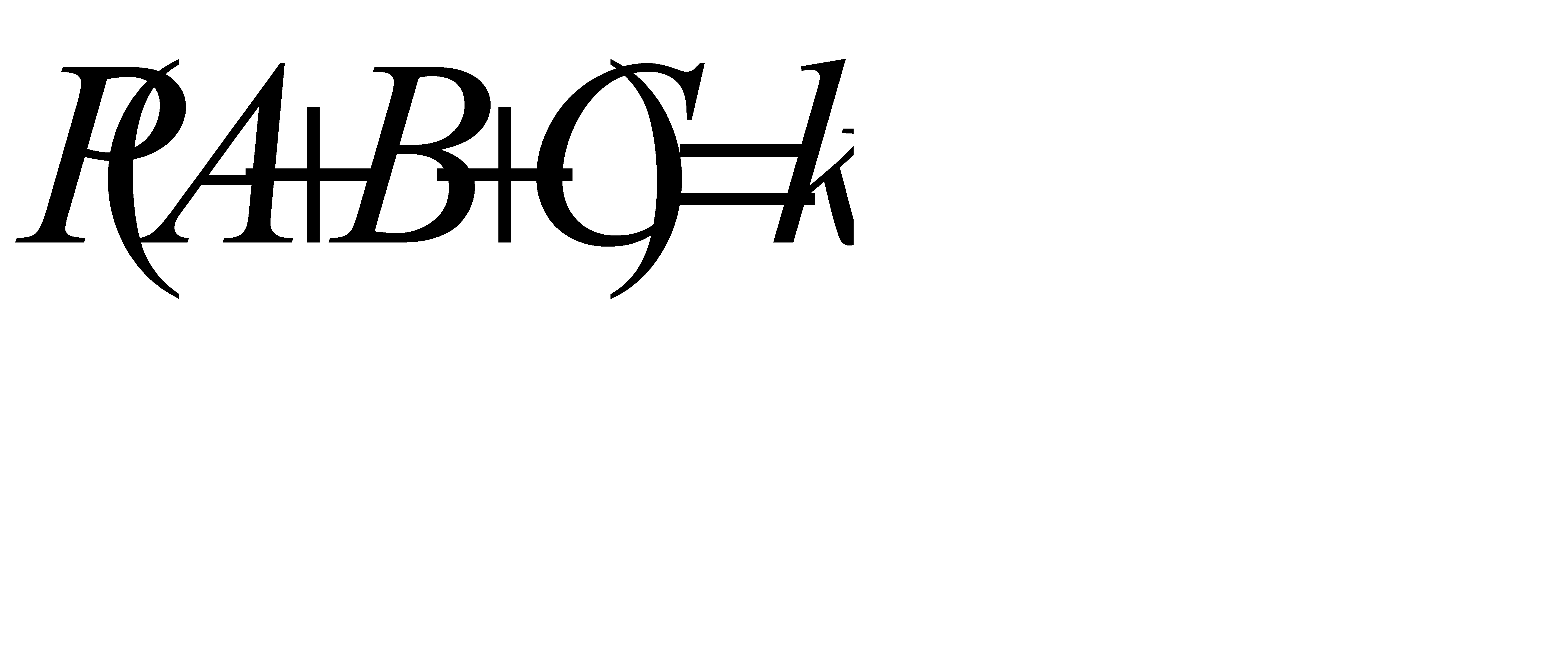 . Выразим
. Выразим 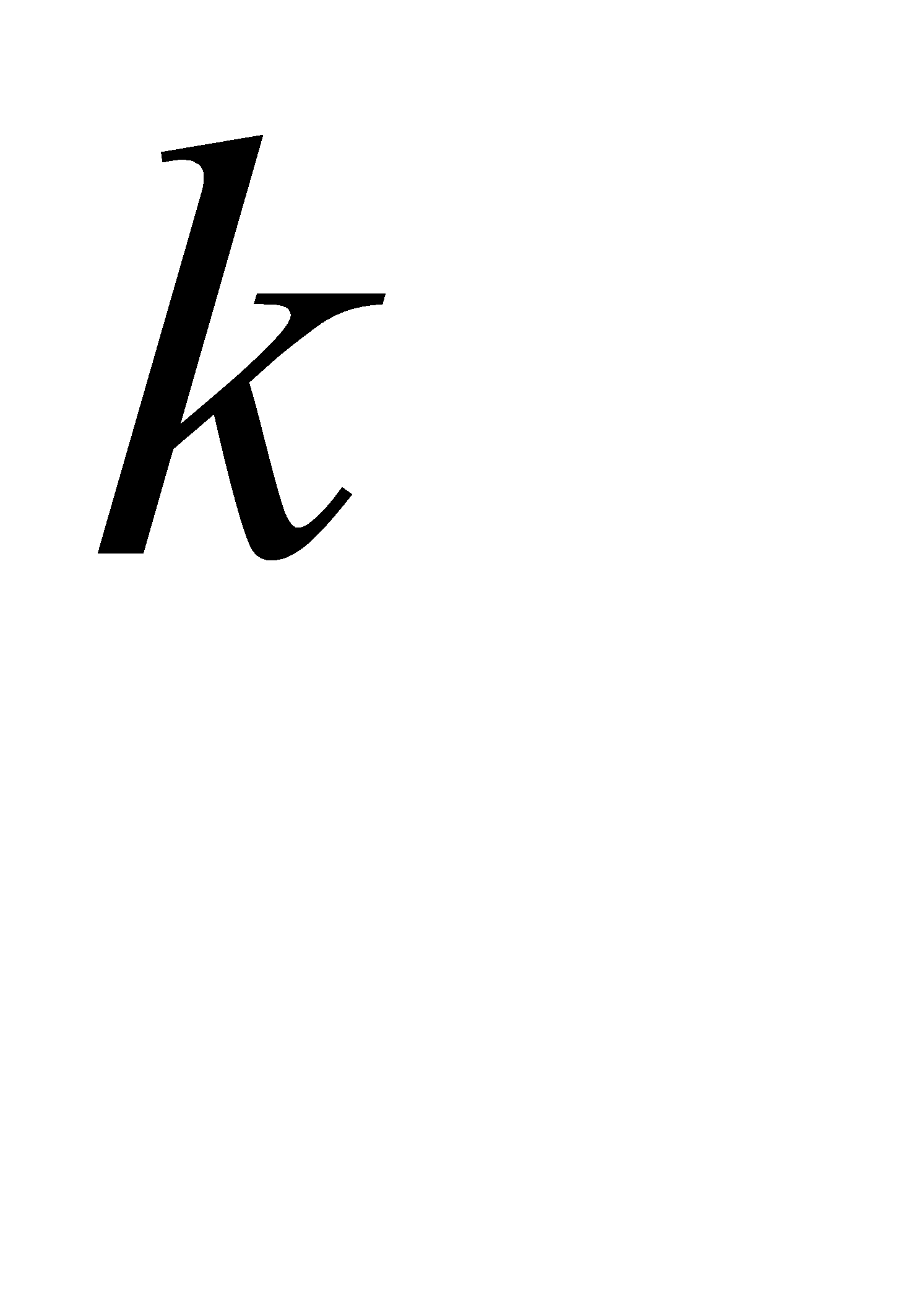 через
через 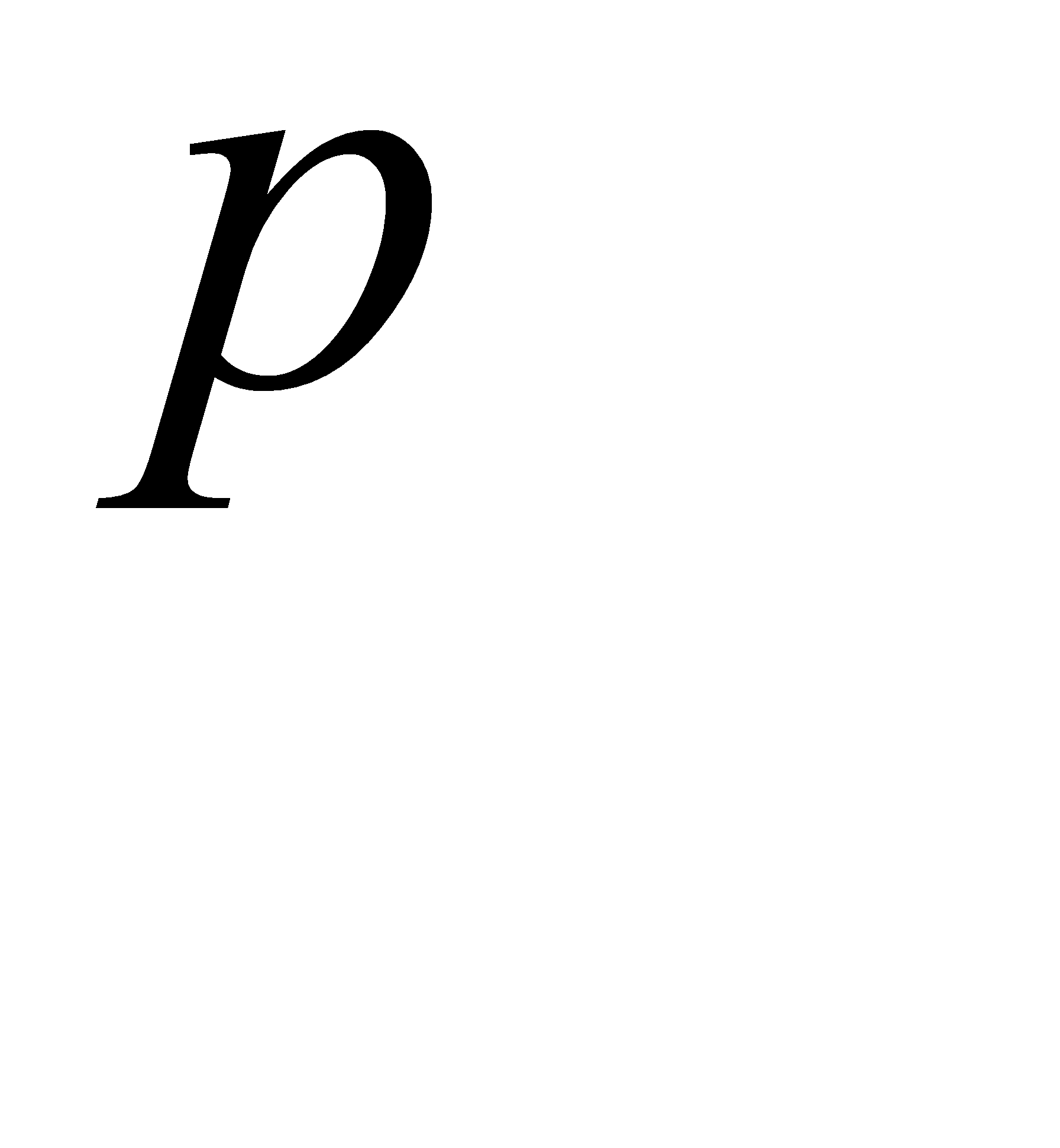 , пользуясь теоремой сложения для трёх несовместных событий:
, пользуясь теоремой сложения для трёх несовместных событий:
 .
.
Решив это уравнение относительно 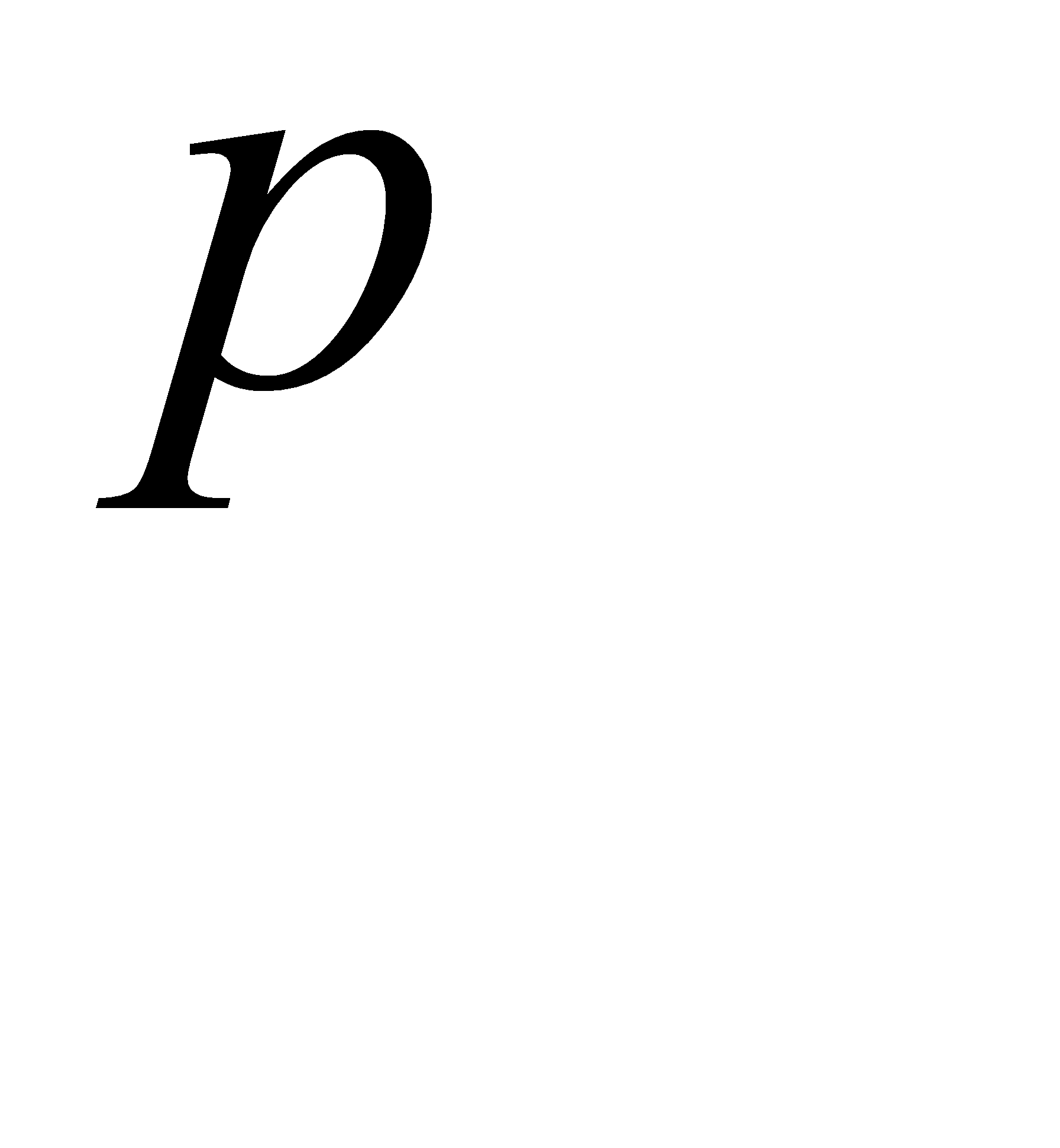 , получим
, получим 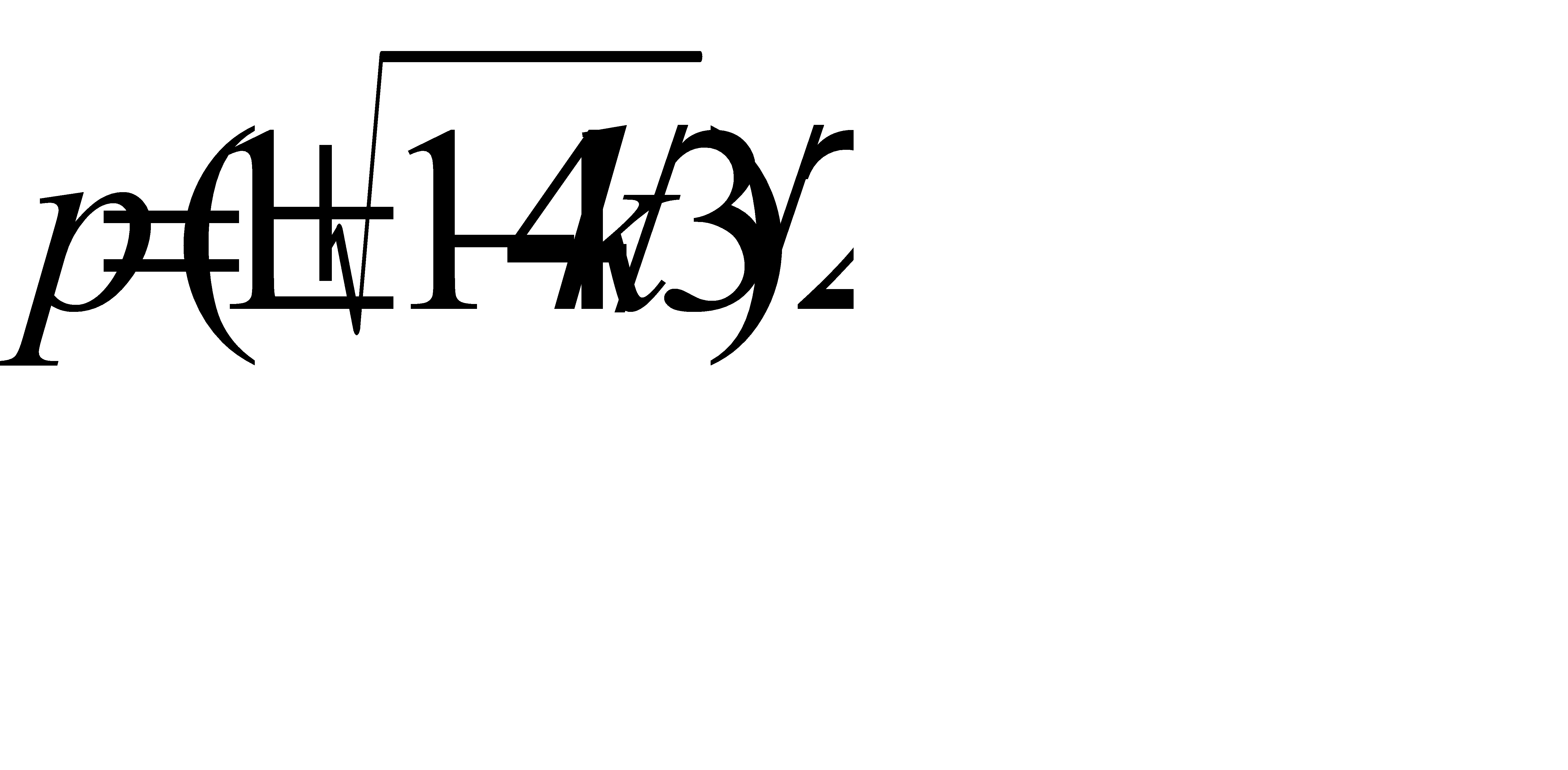 .
.
В таком случае 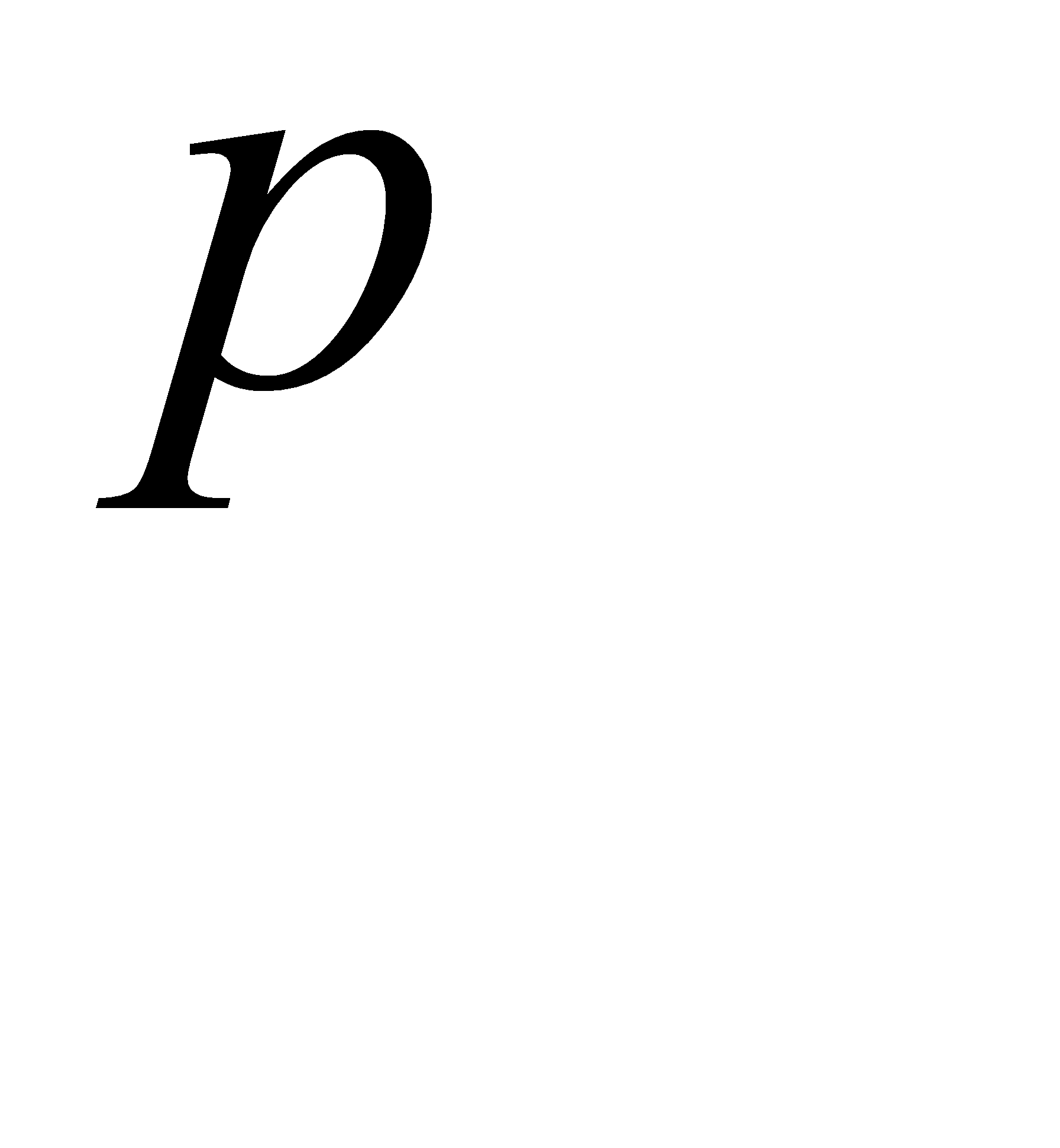 достигает максимального значения
достигает максимального значения 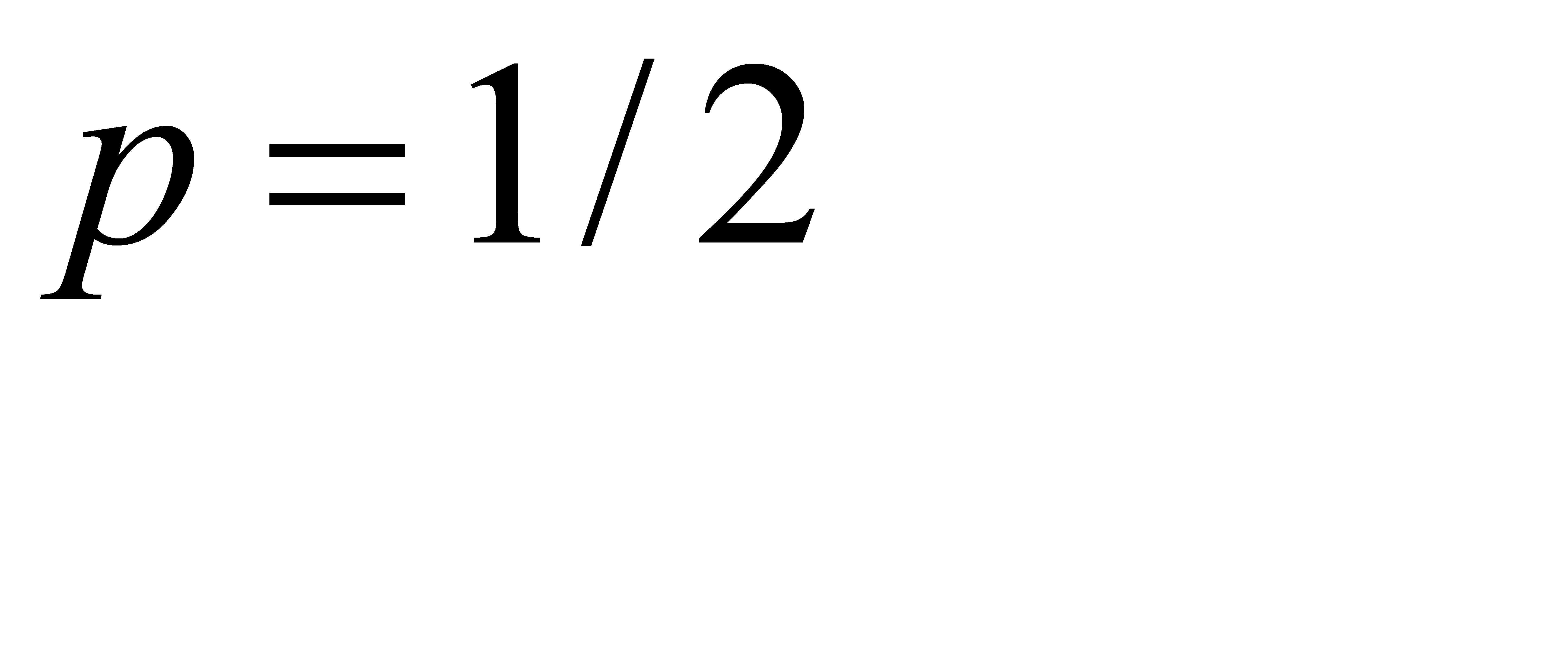 (при
(при  ).
).
Если 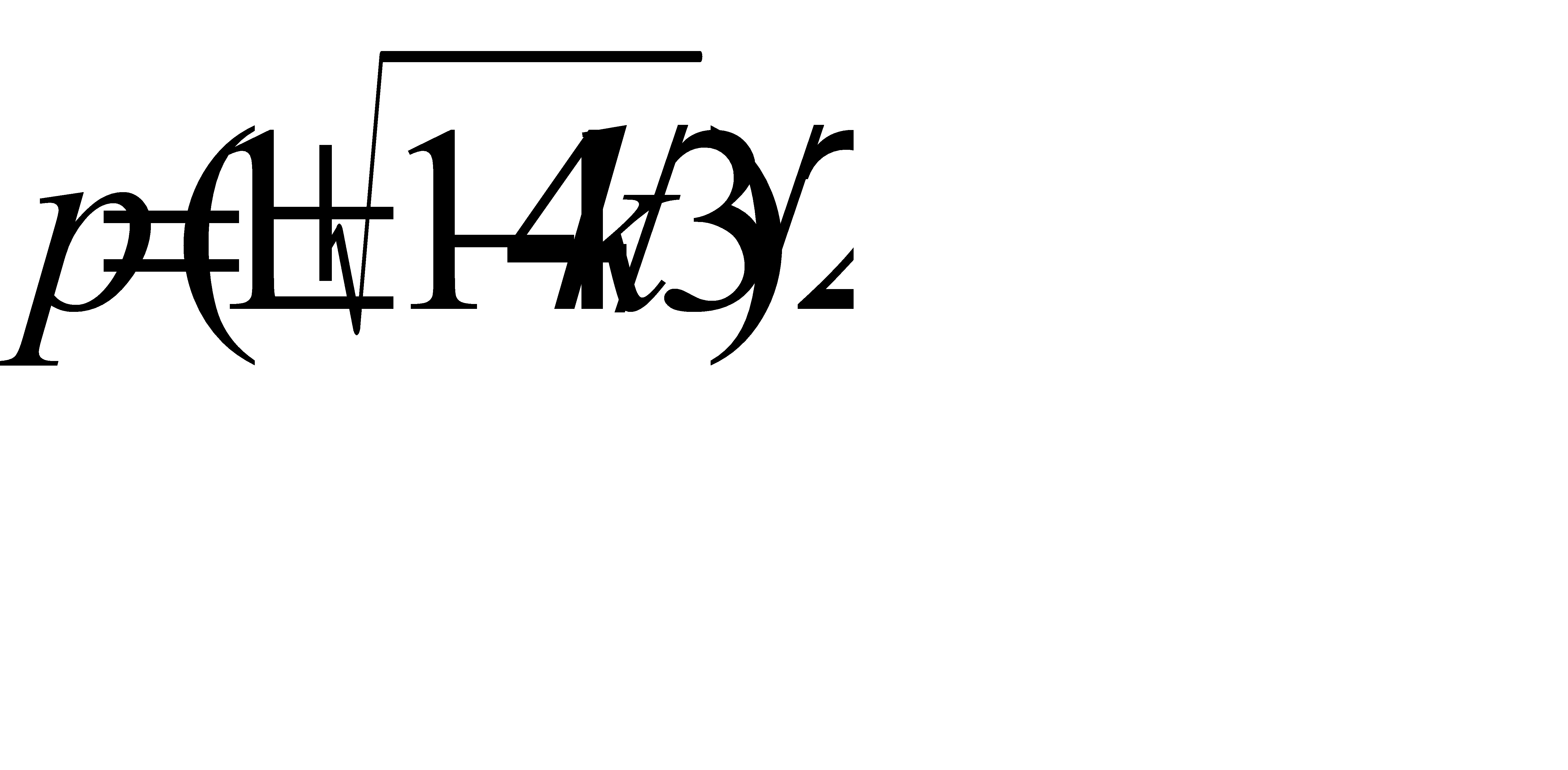 , то, на первый взгляд,
, то, на первый взгляд, 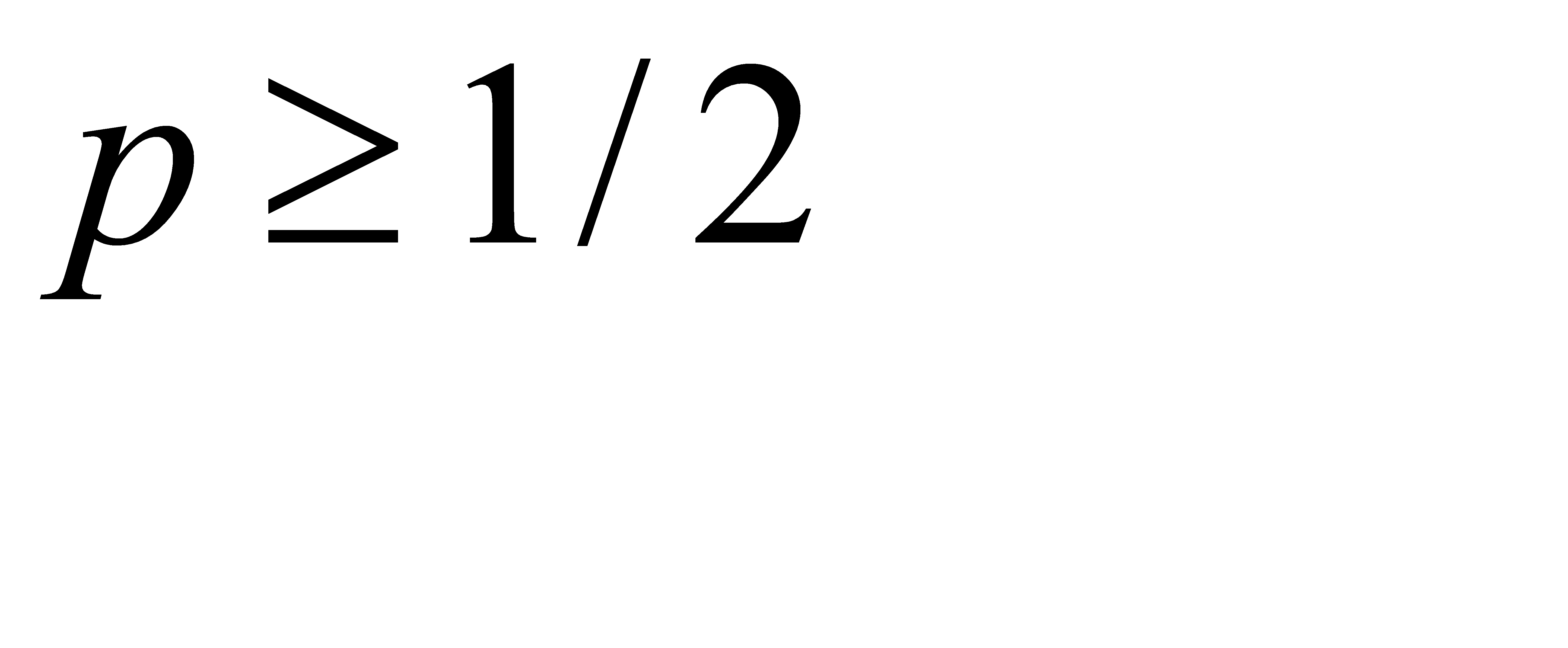 . Покажем, что допущение
. Покажем, что допущение 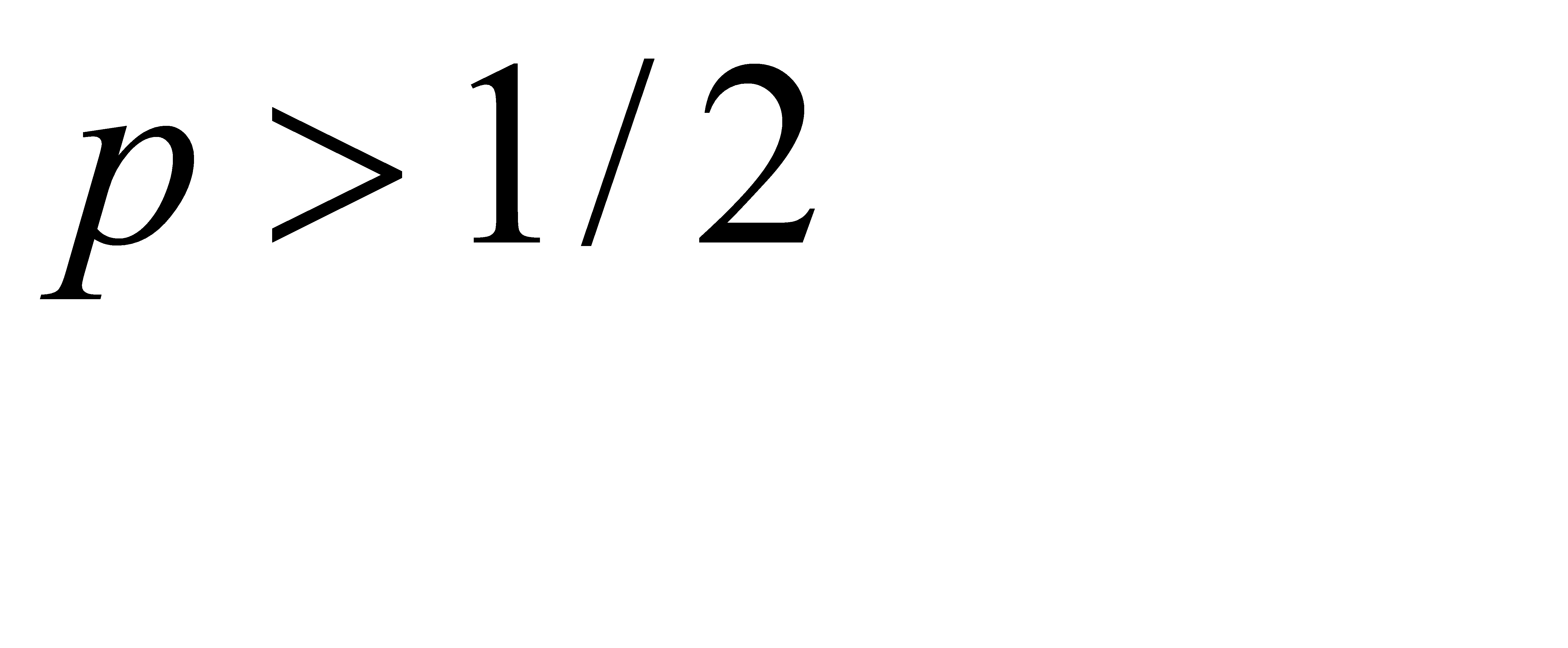 приводит к противоречию. Действительно,
приводит к противоречию. Действительно, 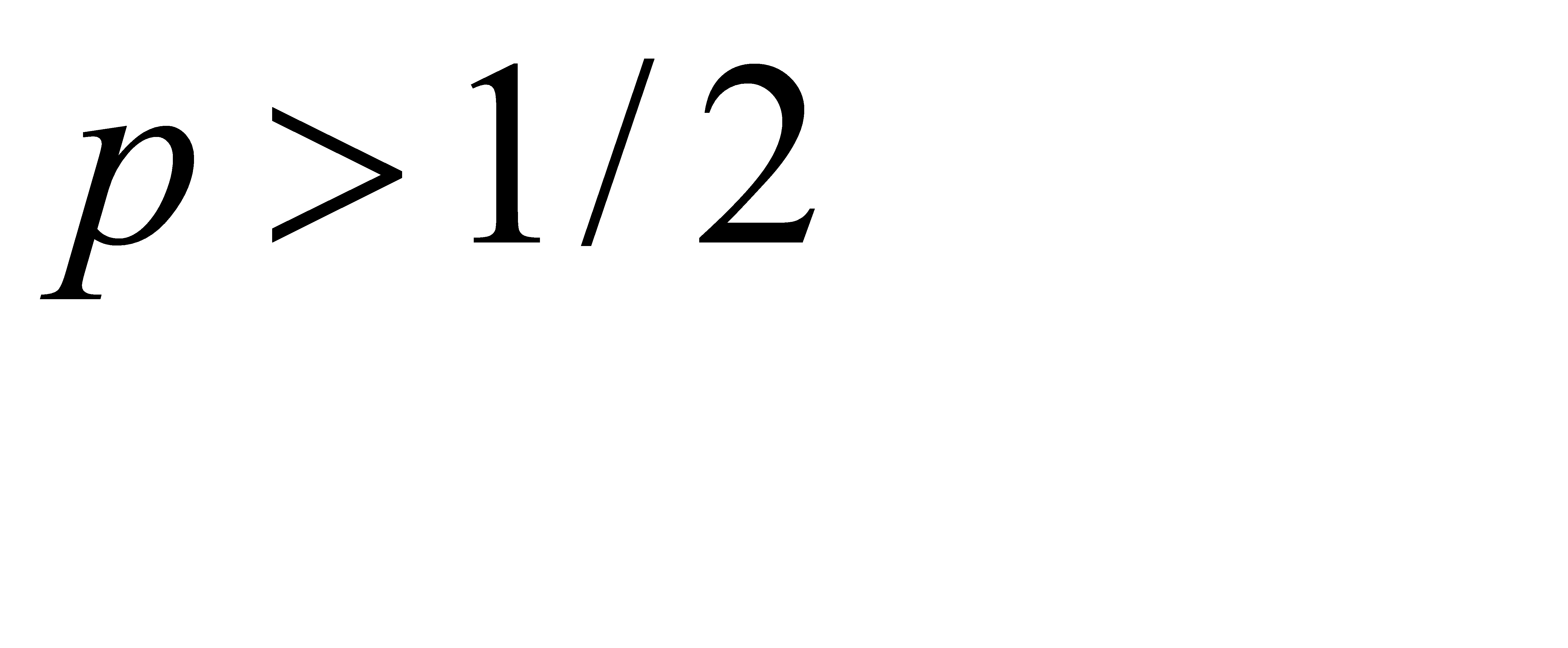 при условии, что
при условии, что 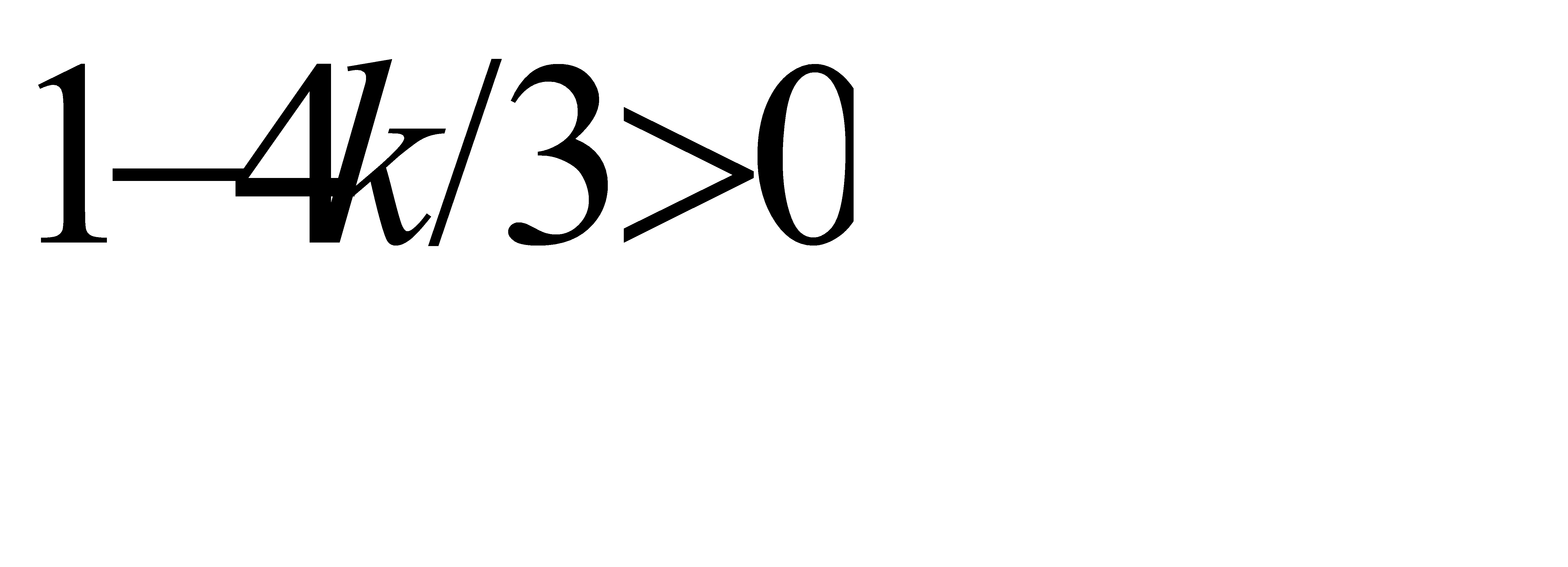 ; или, так как
; или, так как 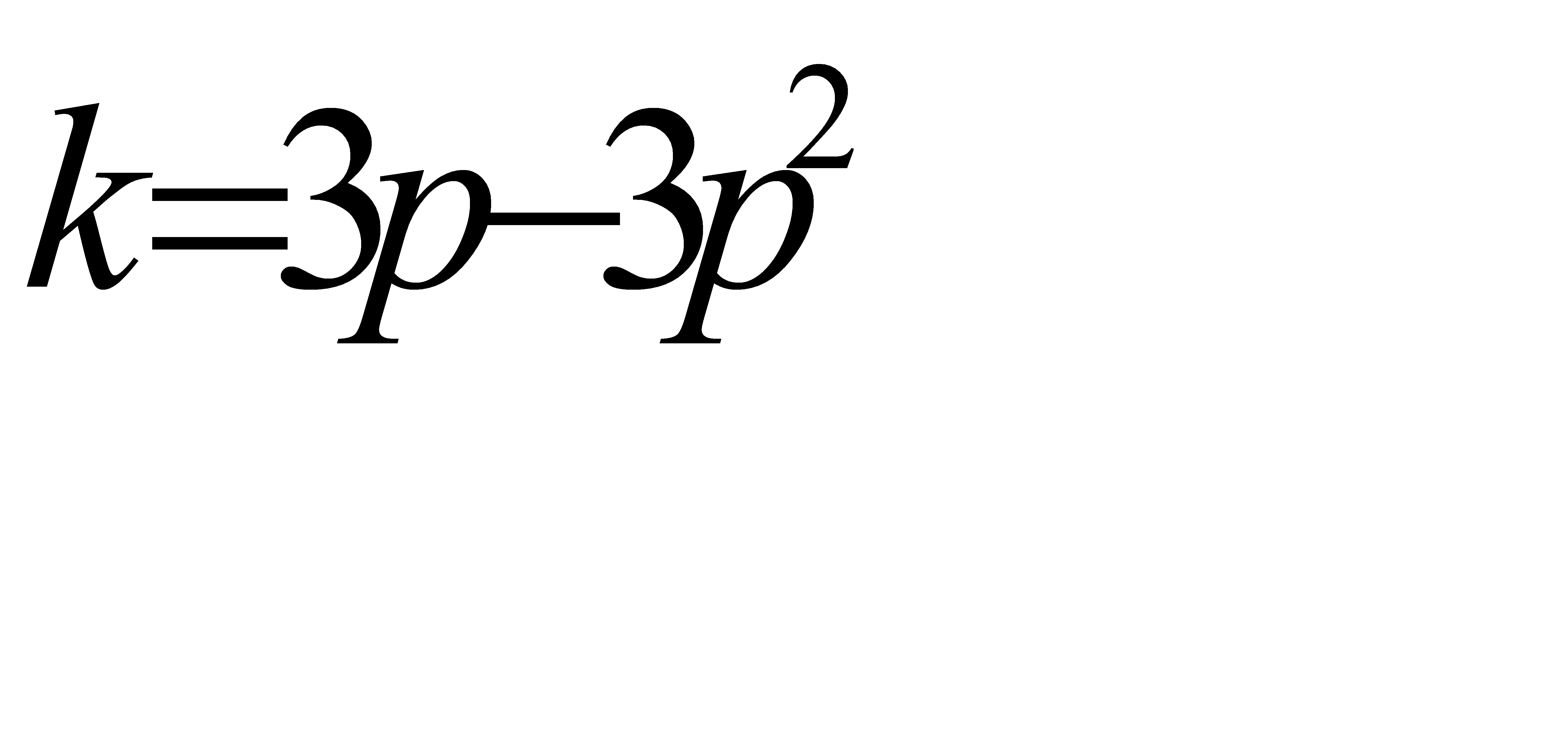 , при условии, что
, при условии, что 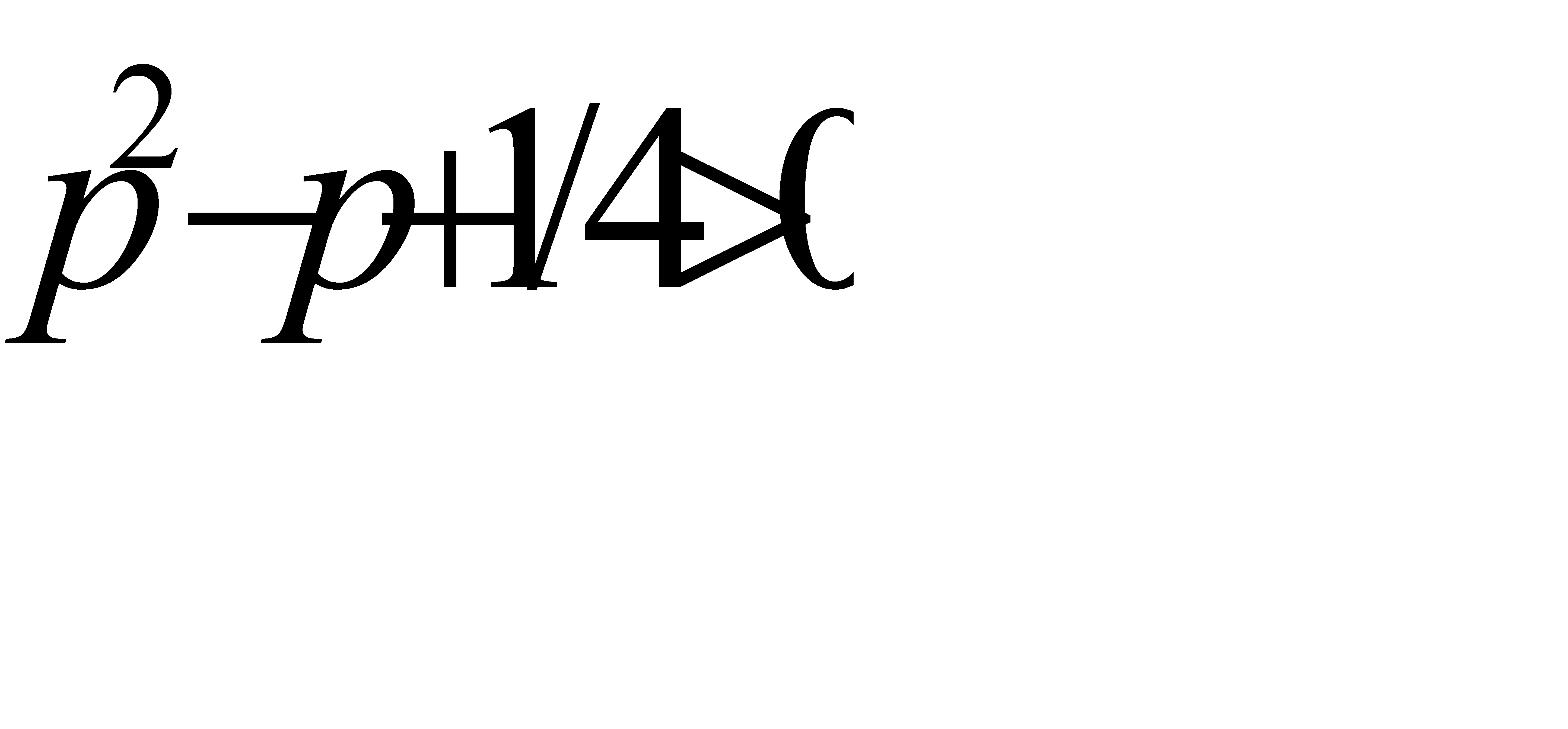 . Отсюда
. Отсюда  .
.
Итак, наибольшее возможное значение 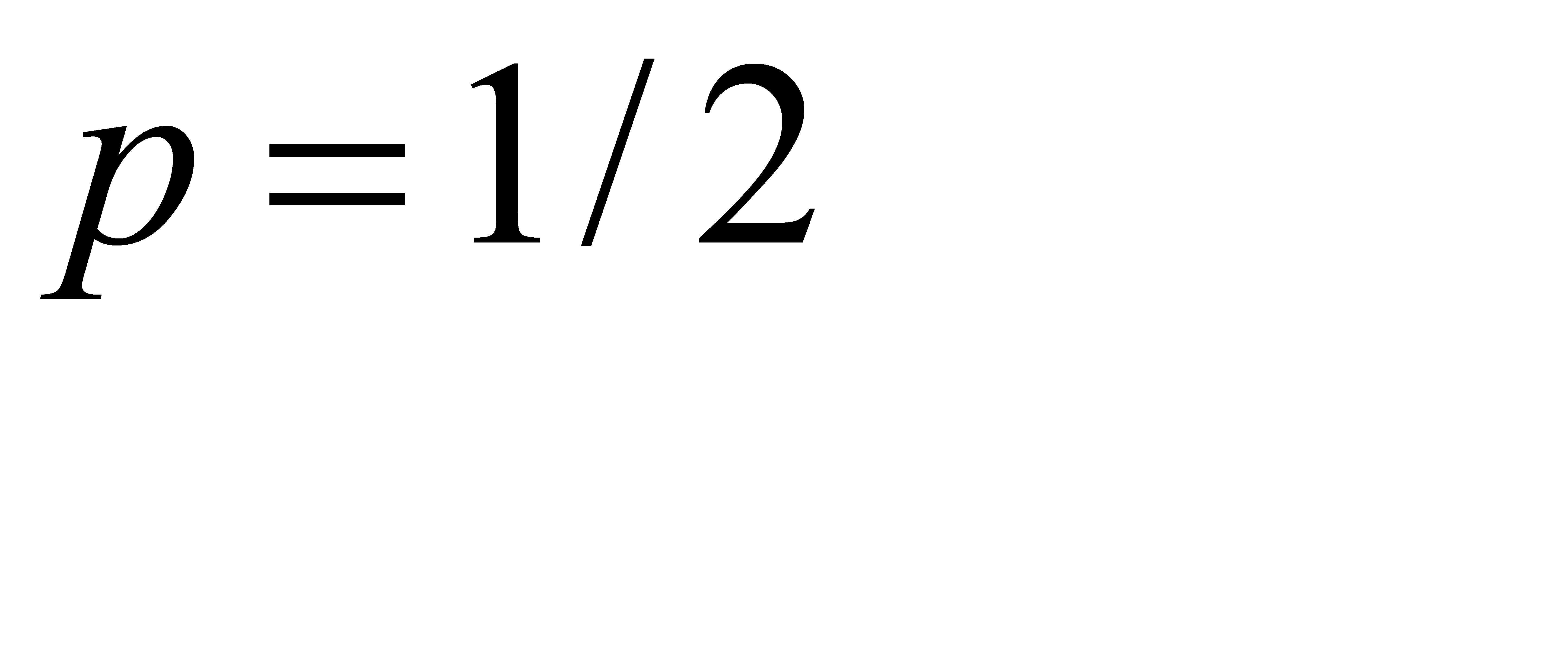 .
.
№80
Вероятность отказа первого элемента равна 0,1,второго -0,15,третьего – 0,2
То есть  =0,1,
=0,1,  =0,15,
=0,15, 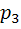 =0,2
=0,2
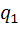 =0,9,
=0,9, 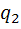 =0,85,
=0,85, 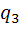 =0,8
=0,8
Тока в цепи не будет, если откажет хотя бы один элемент
То есть нужно использовать формулу появления хотя бы одного события (P(A)=1- 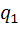 *…*
*…* 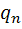 )
)
Значит, искомая вероятность равна 0,388
(P(A)=1- 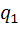 *
* 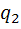 *
* 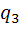 =1-(0,9*0,85*0,8)=0,388)
=1-(0,9*0,85*0,8)=0,388)
Ответ:0,388
№81 Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
Решение:
Вероятность того, что откажет 1й элемент, 2й элемент или оба, обратна вероятности того, что ни один не откажет, т.е.:
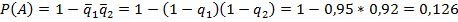
Ответ: 0,126.
№82 Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,6; 0,7.
Решение:
При последовательном сбрасывании четырех бомб мост будет разрушен (событие А), если в него попадет хотя бы одна бомба. Следовательно, искомая вероятность равна:
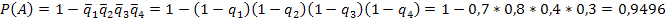
Ответ: 0,9496.
№83 Три исследователя, независимо один от другого, производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора, равна 0,1. Для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку.
Решение.
Вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку равна:
Р(А) = 1 - q1q2q3 = 1 –(1 – 0,1)*(1 – 0,15)*(1 – 0,2) = 0,388.
№84 Вероятность успешного выполнения упражнения для каждого из двух спортсменов равна 0,5. Спортсмены выполняют упражнение по очереди, причем каждый делает по две попытки. Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами.
Решение.
Для вручения приза достаточно, чтобы хотя бы
одна из четырех попыток была успешной. Вероятность успешной
попытки р = 0,5, а неуспешной q=1 - 0,5 = 0,5. Искомая вероятность
Р = 1 - q^4 = 1 —0,5^4 =0,9375.
№85 Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.
Решение.
Для получения приза достаточно, чтобы хотя бы одна из четырех попыток была успешна. Вероятность успешной попытки p=0,3 , неуспешной q=1-p=0,7. Тогда искомая вероятность будет равна P=1-q*q*q*q=1- 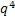 ≈0,76
≈0,76
№86 Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле.
Решение:
Вероятность попадания в мишень хотя бы при одном из трех выстрелов (событие А) равна
Р(А)=1-q3, где q — вероятность промаха. По условию, P (A) = 0,875. Следовательно,
0,875=1—q3, или q3 = 1—0,875 = 0,125.
Отсюда q= 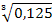 =0,5.
=0,5.
Искомая вероятность р = 1— q = 1—0,5 = 0,5.
№87 Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
Решение:
Вероятность попадания в мишень хотя бы при одном из трех выстрелов (событие А) равна
Р(А)=1-q4, где q — вероятность промаха. По условию, P (A) = 0,9984. Следовательно,
0,9984=1—q4, или q4 = 1—0,9984= 0,0016.
Отсюда q= 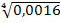 =0,2.
=0,2.
Искомая вероятность р = 1— q = 1—0,2 = 0,8.
№88 Многократно измеряют некоторую физическую величину. Вероятность того, что при считывании показаний прибора допущена ошибка, равна 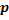 . Найти наименьшее число измерений, которое необходимо произвести, чтобы с вероятностью
. Найти наименьшее число измерений, которое необходимо произвести, чтобы с вероятностью 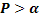 можно было ожидать, что хотя бы один результат измерений окажется неверным.
можно было ожидать, что хотя бы один результат измерений окажется неверным.
Решение:
Вероятность хотя бы одной ошибки из 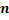 считываний равна
считываний равна 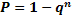 , где
, где 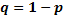 , и
, и 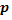 - вероятность ошибки при одном считывании. Из условия
- вероятность ошибки при одном считывании. Из условия 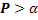 получим:
получим:
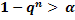 ;
; 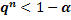 ;
; 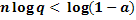 ;
; 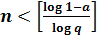
Следовательно, искомое число измерений равно 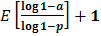 , где
, где 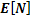 – целая часть числа
– целая часть числа 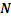
№89 В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется
белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).
Решение:
Обозначим через А событие - извлечен белый шар. Возможны следующие предположения о первоначальном составе шаров: В1 - белых шаров нет, В2 - один белый шар, В3 - два белых шара.
Поскольку всего имеется три гипотезы, причем по условию они равновероятны, и сумма вероятностей гипотез равна единице (так как они образуют полную группу событий), то вероятность каждой из гипотез равна 1/3, т. е. P(B1) = P(B2) = P(B3) = 
Вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне не было белых шаров, 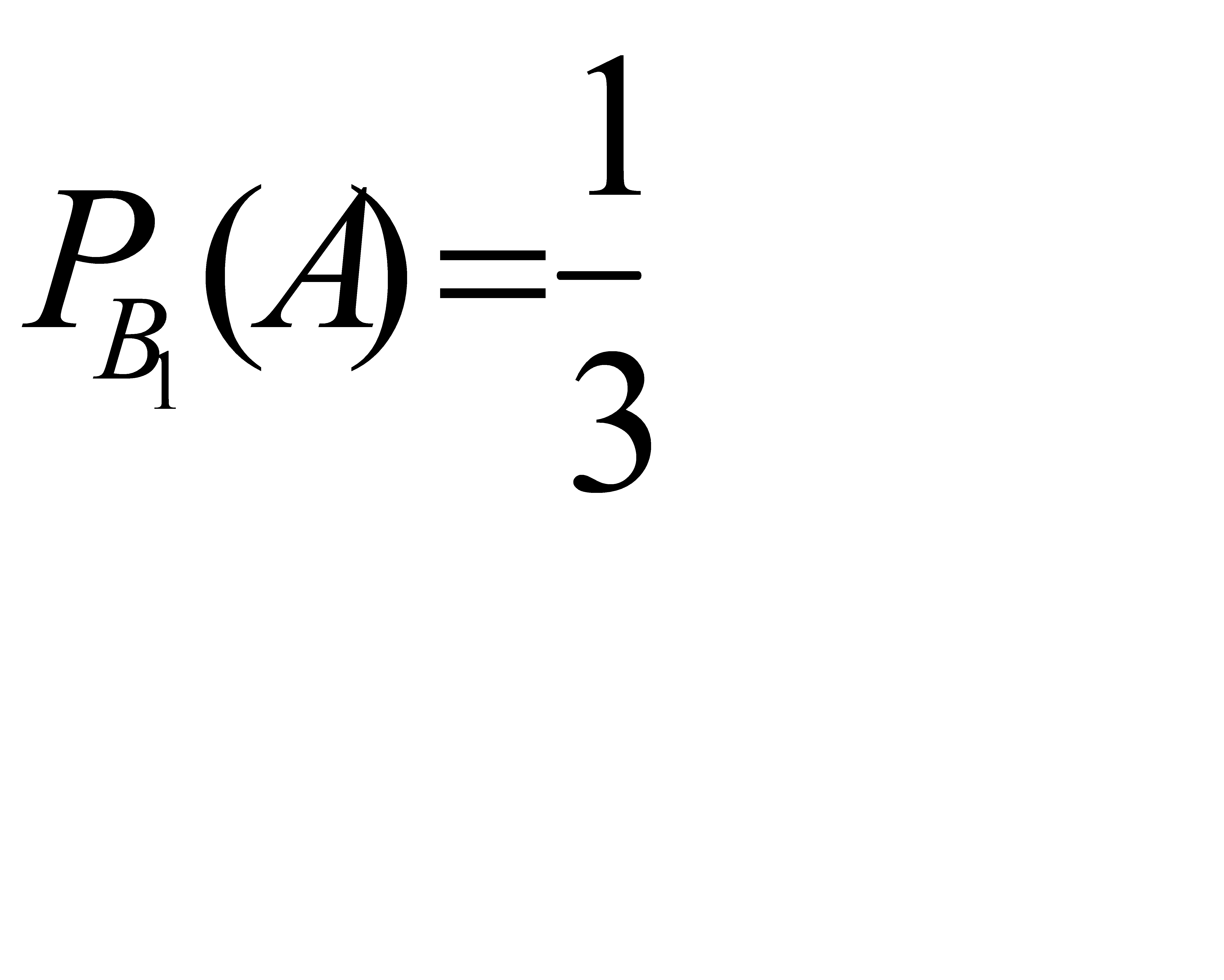 . Если в урне был один белый шар, то
. Если в урне был один белый шар, то 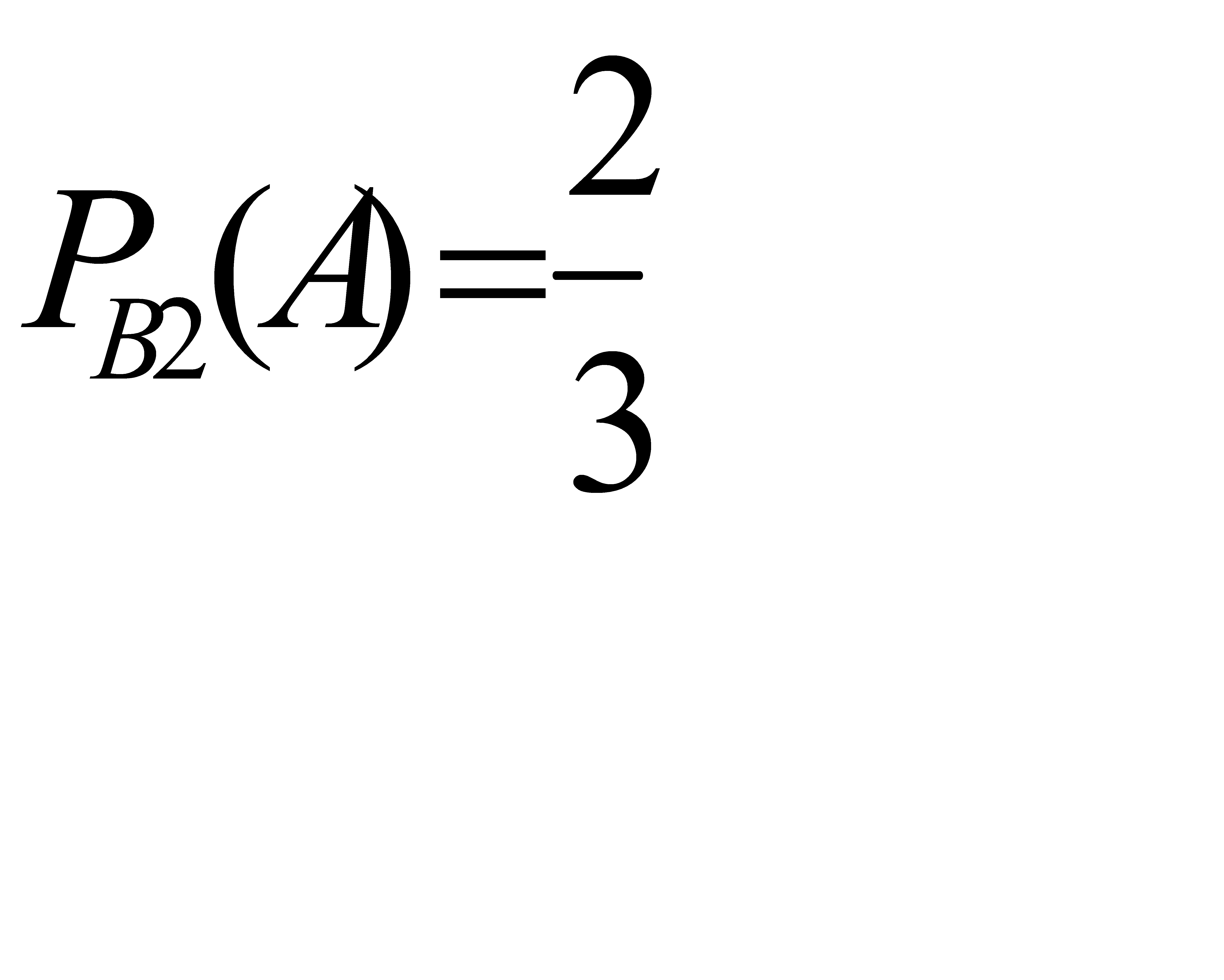 . Условная вероятность того, что будет извлечен белый шар, при условии, что в урне было два белых шара
. Условная вероятность того, что будет извлечен белый шар, при условии, что в урне было два белых шара 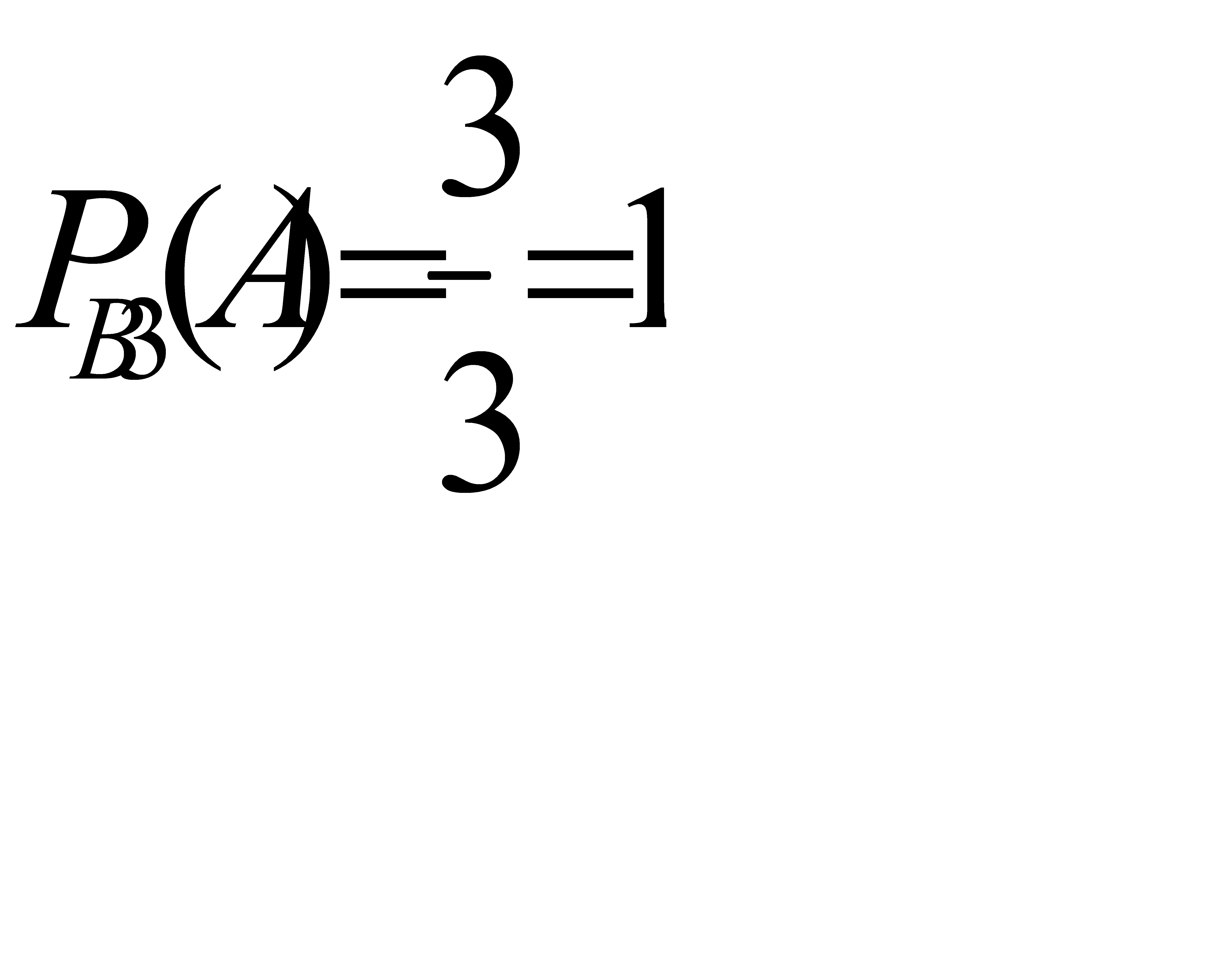
Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:

Ответ: P(A)= 
№90 В урну, содержащую n шаров, опущен белый шар, после наудачу извлечен один шар. Найти вероятность того что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров по цвету.
Решение:
Обозначим через А событие - извлечен белый шар. Возможны следующие предположения о первоначальном составе шаров: В1- 1 белый шар, В2- 2 белых шара... Вn-n белых шаров. Поскольку всего имеется n гипотез, причем по условию они равновозможны и сумма вероятностей равна единице, то вероятность каждой гипотезы равна  . По гипотезе В1 условная вероятность вытащить белый шар равна
. По гипотезе В1 условная вероятность вытащить белый шар равна 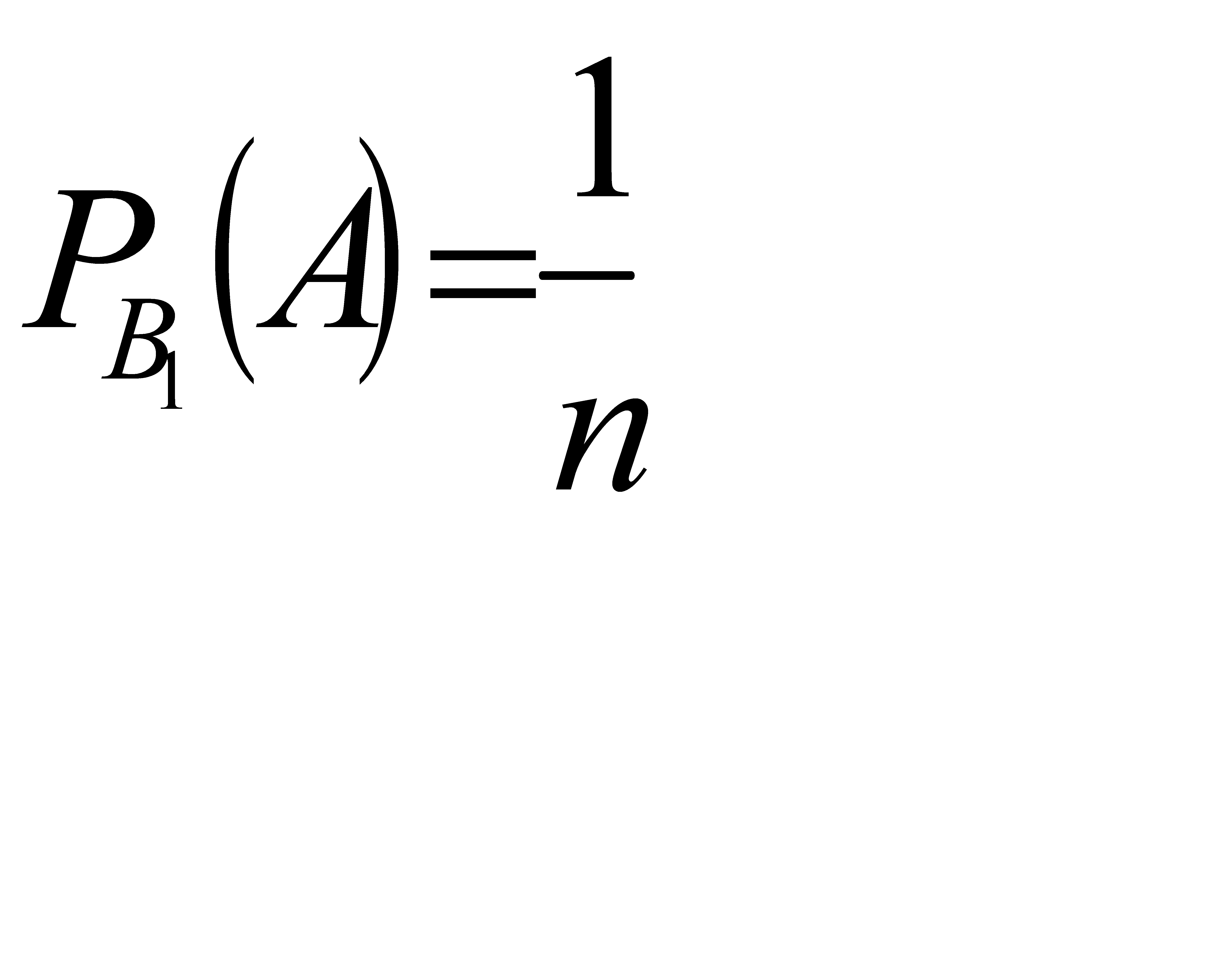 , по гипотезе В2 условная вероятность вытащить белый шар равна
, по гипотезе В2 условная вероятность вытащить белый шар равна 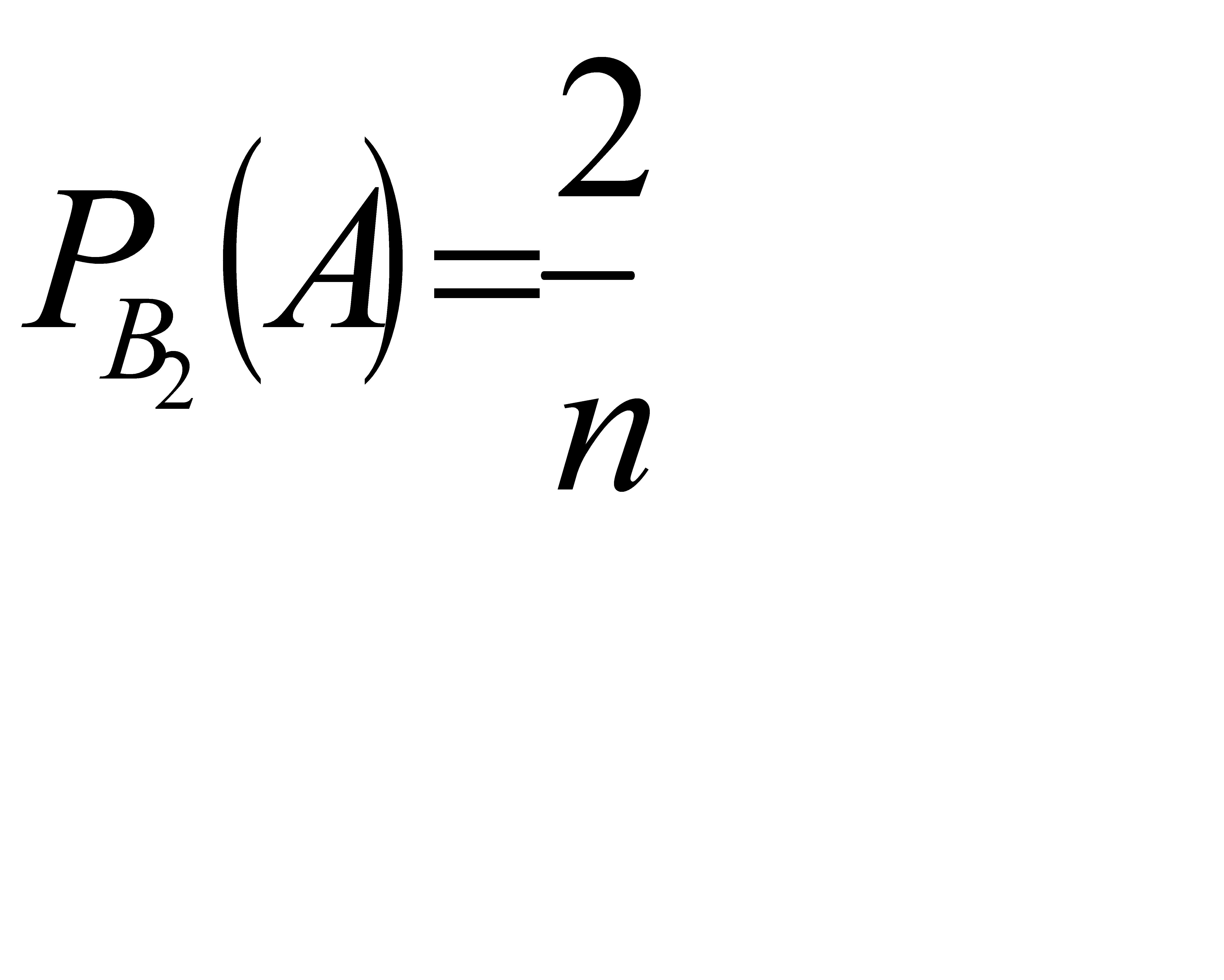 … по гипотезе Вn условная вероятность вытащить белый шар равна
… по гипотезе Вn условная вероятность вытащить белый шар равна 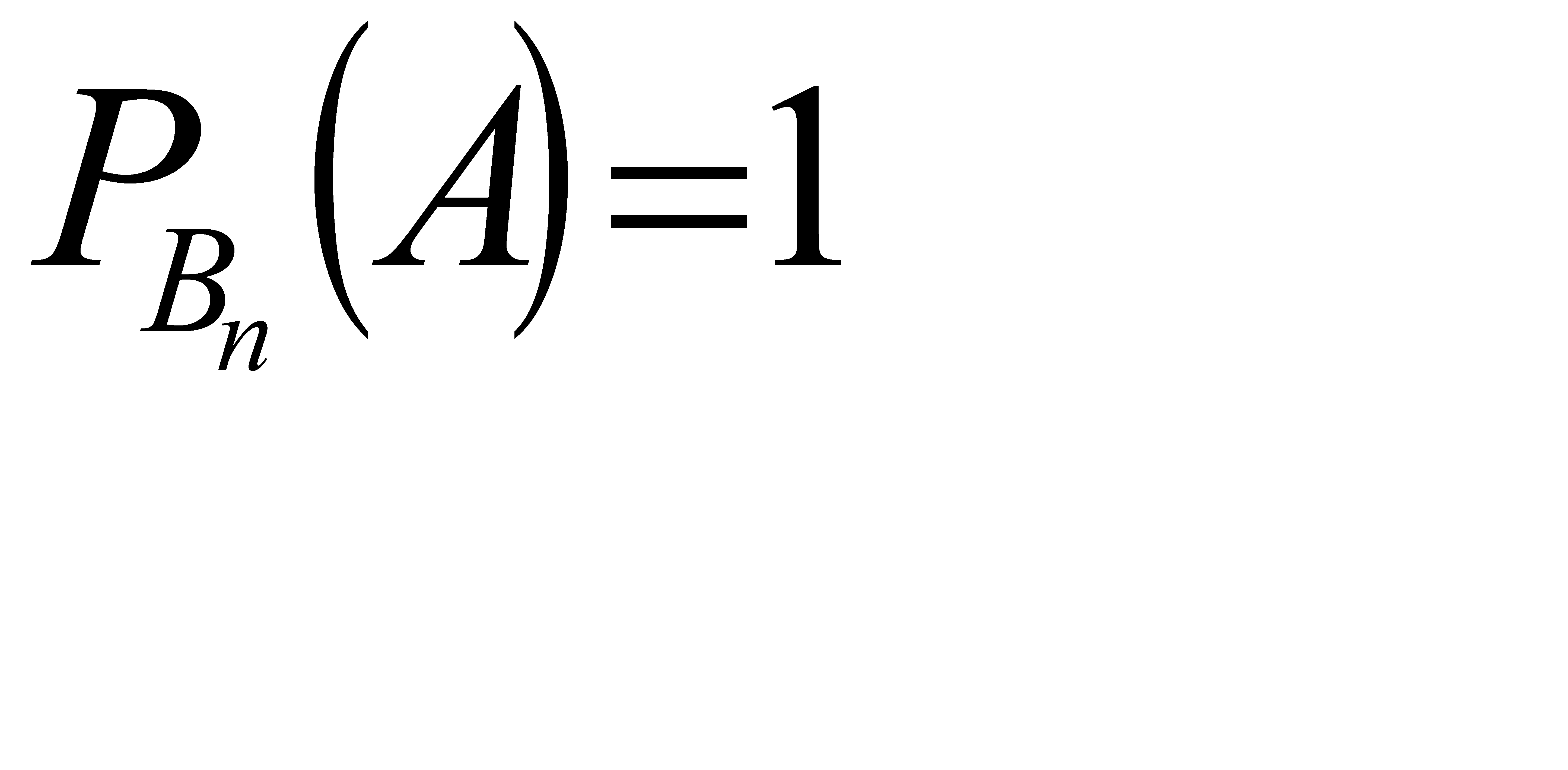 .
.
Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:

Ищенко Марина
№91 В вычислительной лаборатории имеется шесть клавишных автоматов и четыре полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 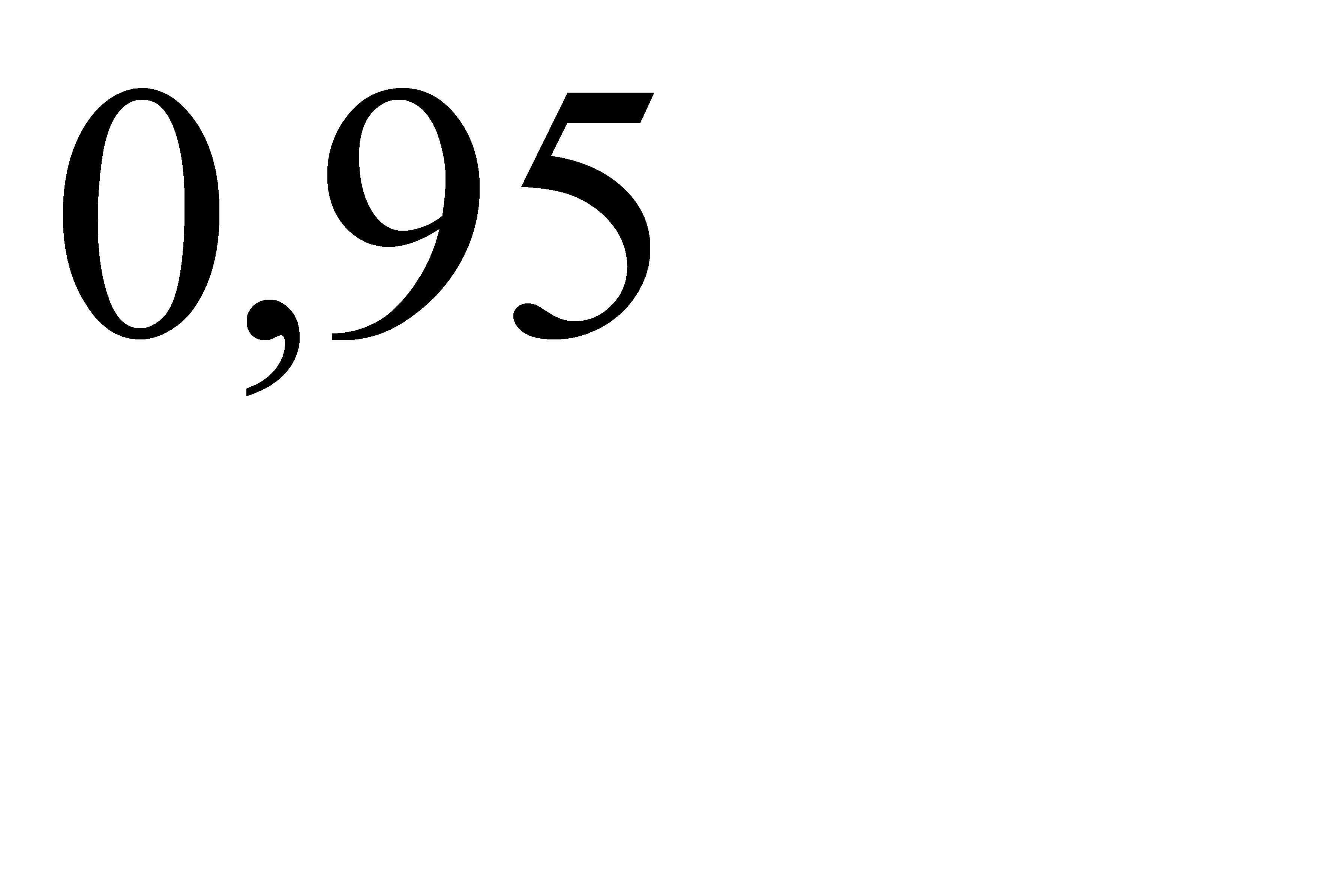 ; для полуавтомата эта вероятность равна
; для полуавтомата эта вероятность равна 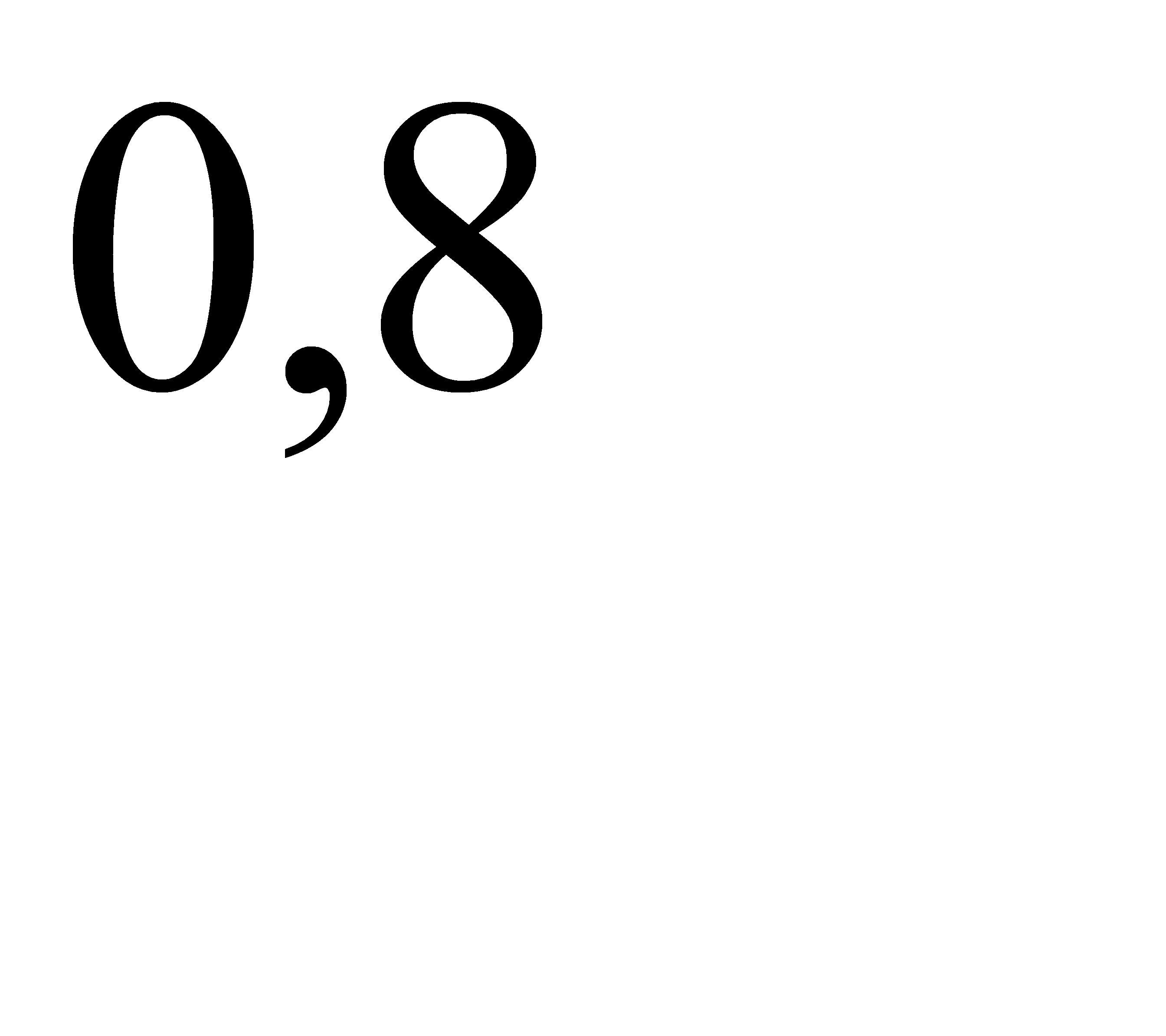 . Студент производит расчет на наудачу выбранной машине. Найти вероятность того, что до окончания расчета машина не выйдет из строя.
. Студент производит расчет на наудачу выбранной машине. Найти вероятность того, что до окончания расчета машина не выйдет из строя.
Решение
Обозначим через  событие – произведен расчет на наудачу выбранной машине. Возможны следующие гипотезы в данном эксперименте:
событие – произведен расчет на наудачу выбранной машине. Возможны следующие гипотезы в данном эксперименте:  - расчет производится на клавишном автомате,
- расчет производится на клавишном автомате, 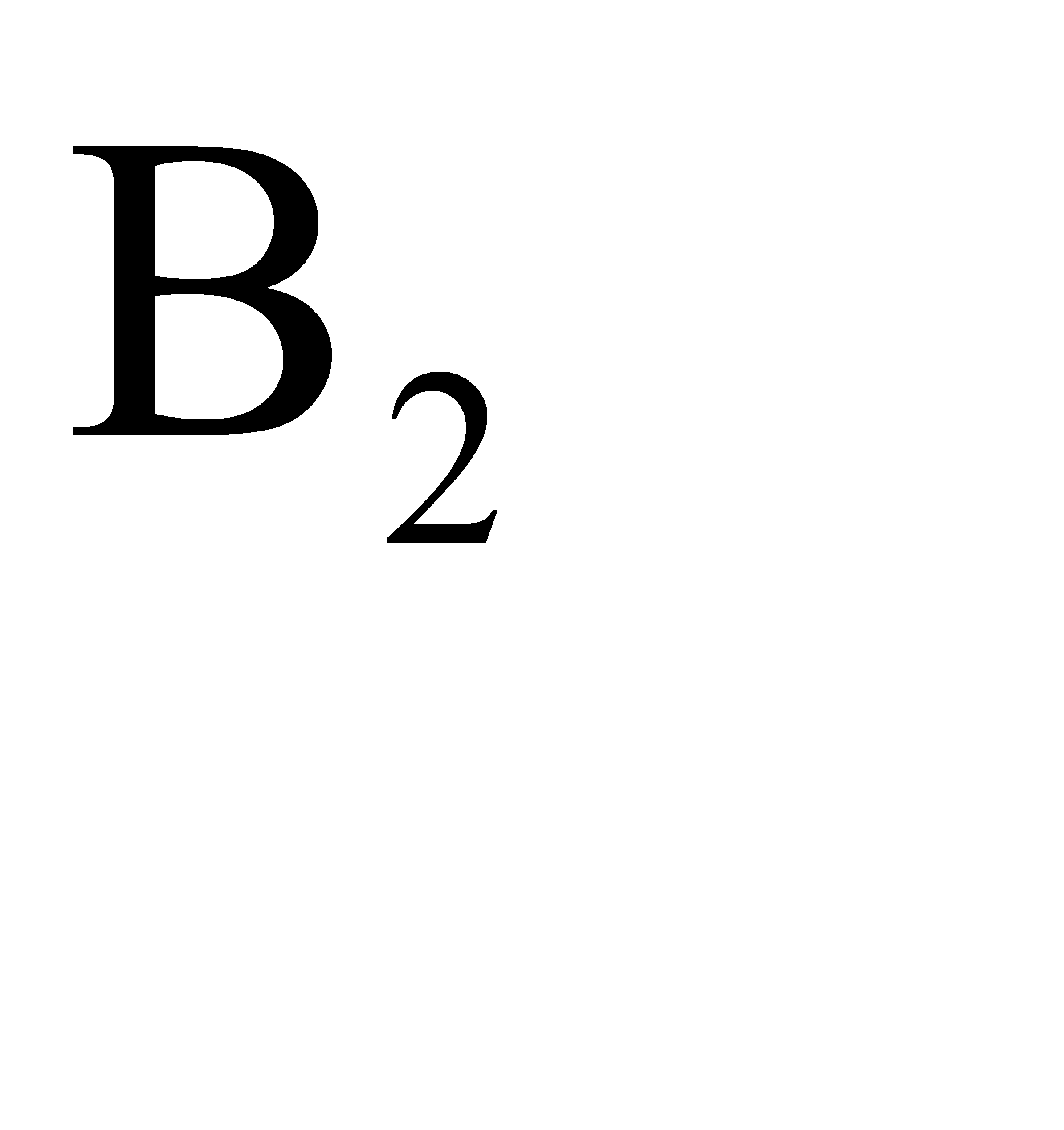 - расчет производится на полуавтомате.
- расчет производится на полуавтомате.
Так как имеется 6 клавишных автоматов и 4 полуавтомата, то вероятность того, что произойдет гипотеза  , равна
, равна 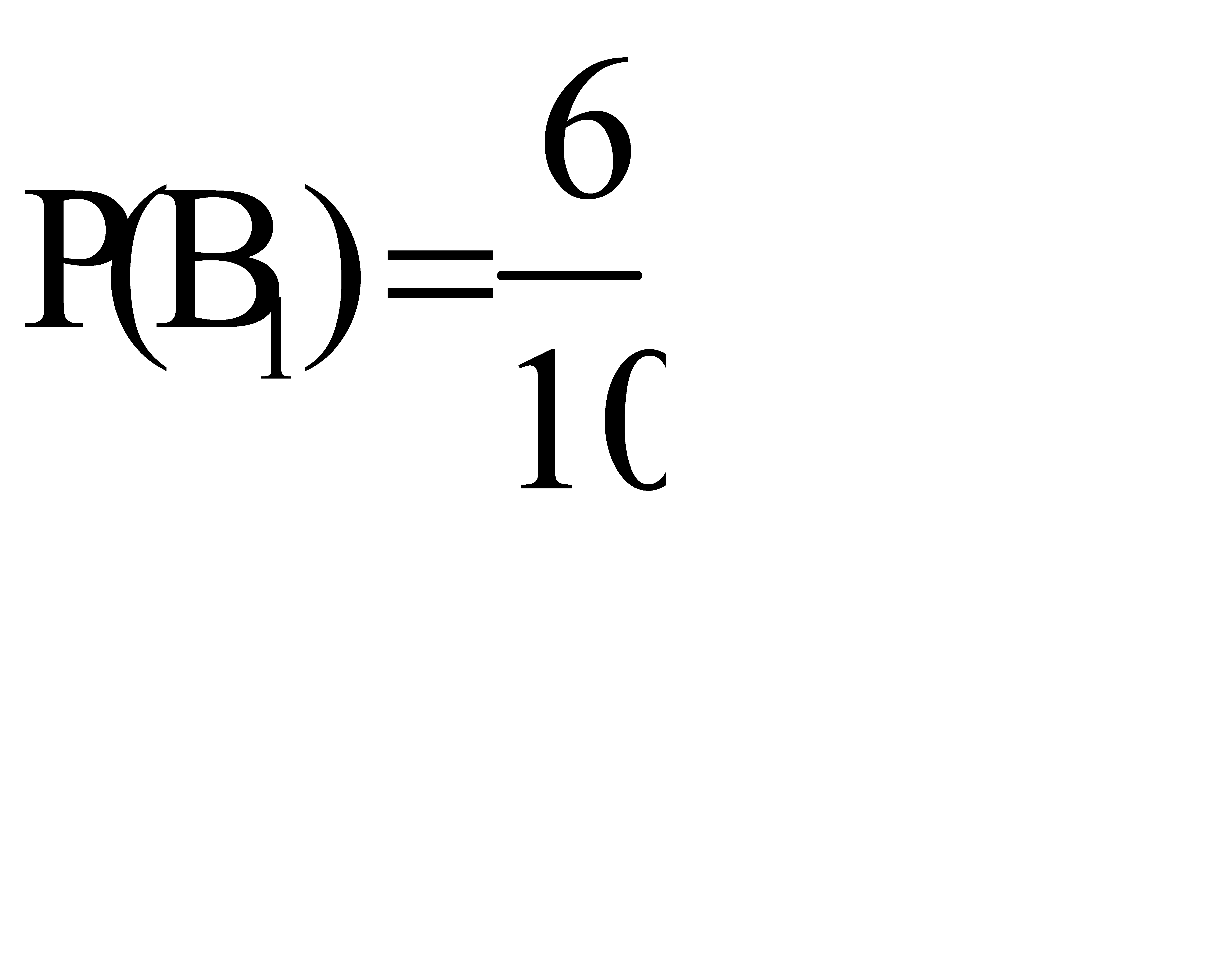 . А вероятность того, что произойдет гипотеза
. А вероятность того, что произойдет гипотеза 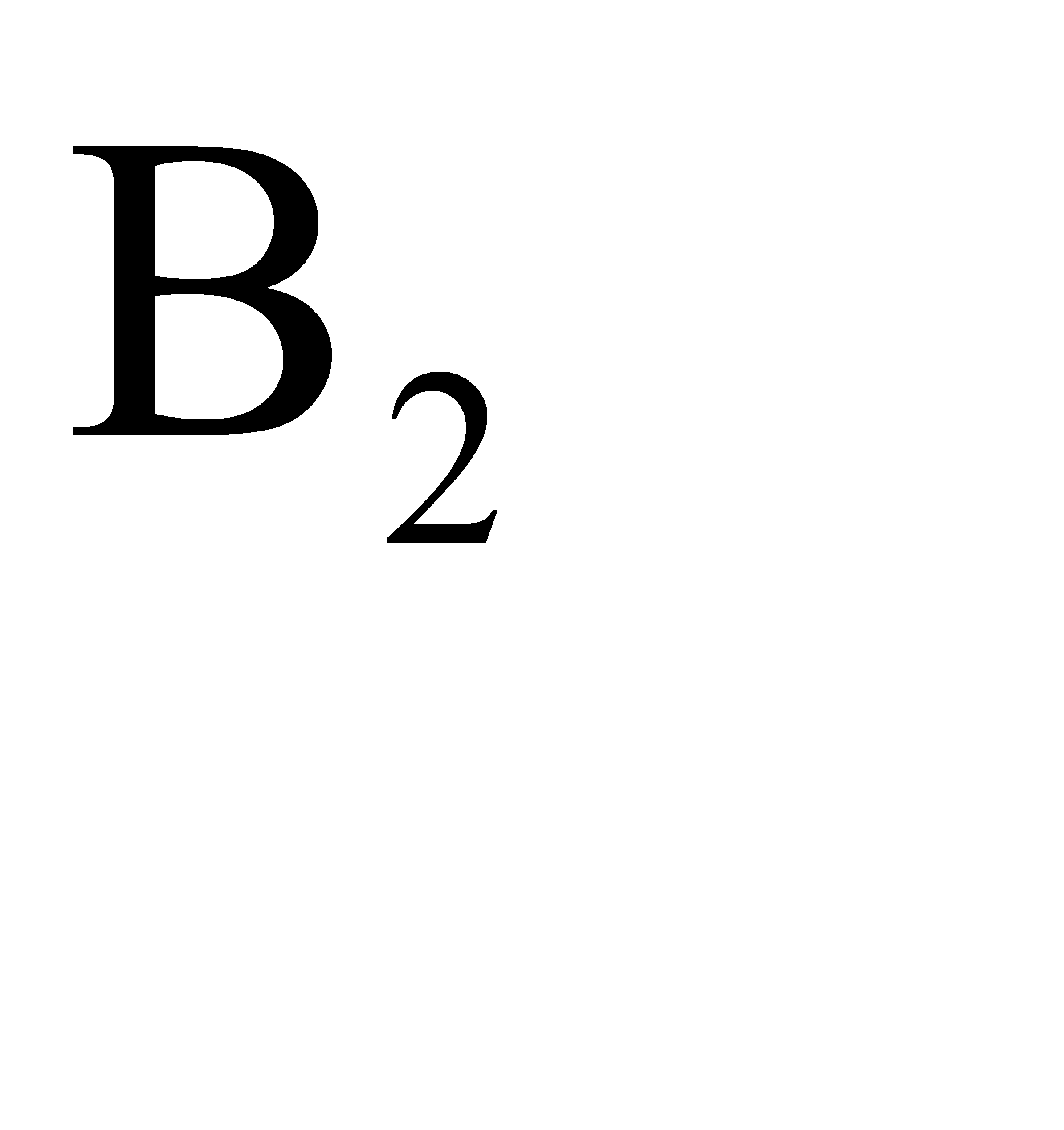 , равна
, равна 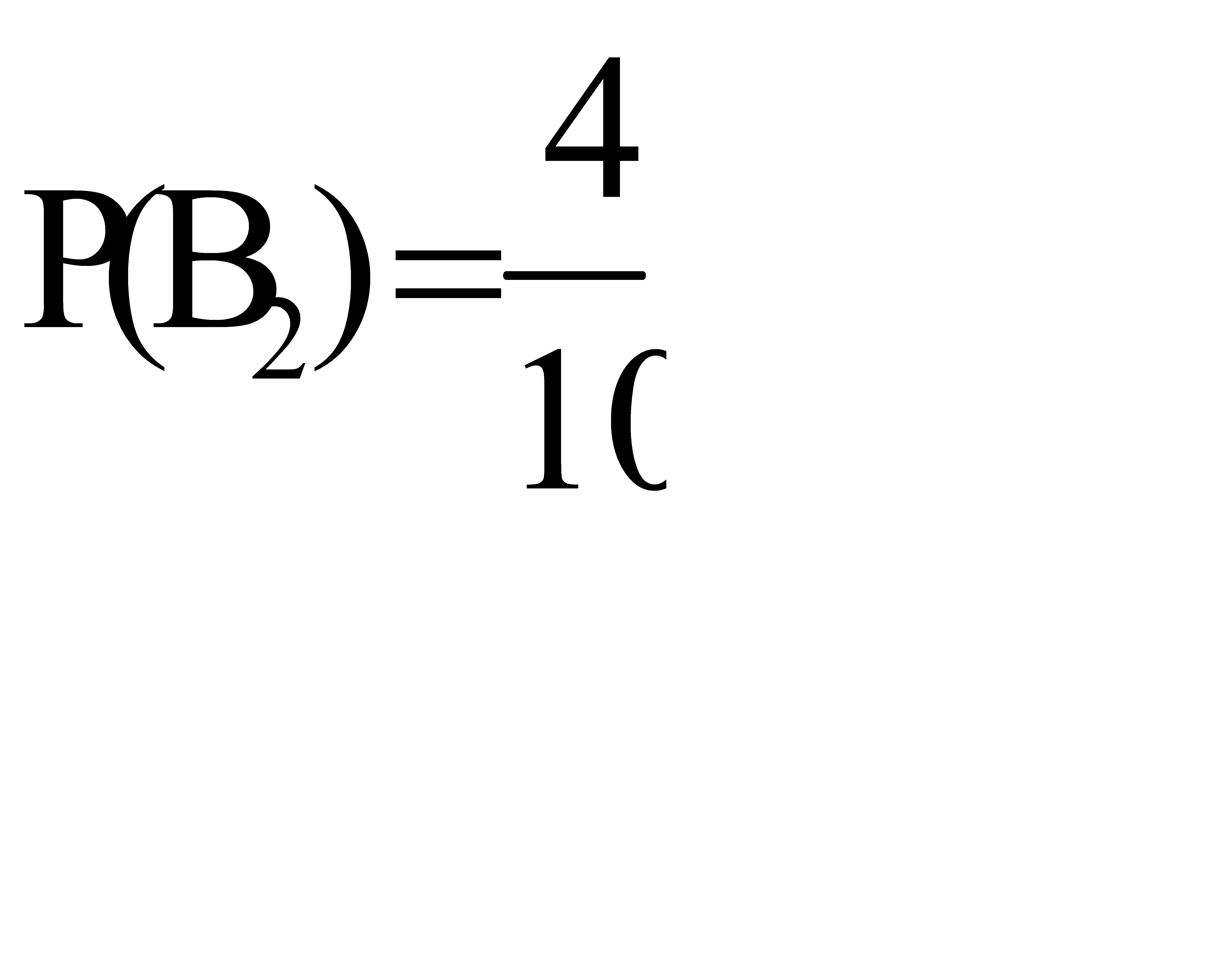 .
.
Условная вероятность того, что клавишный автомат не выйдет из строя, равна 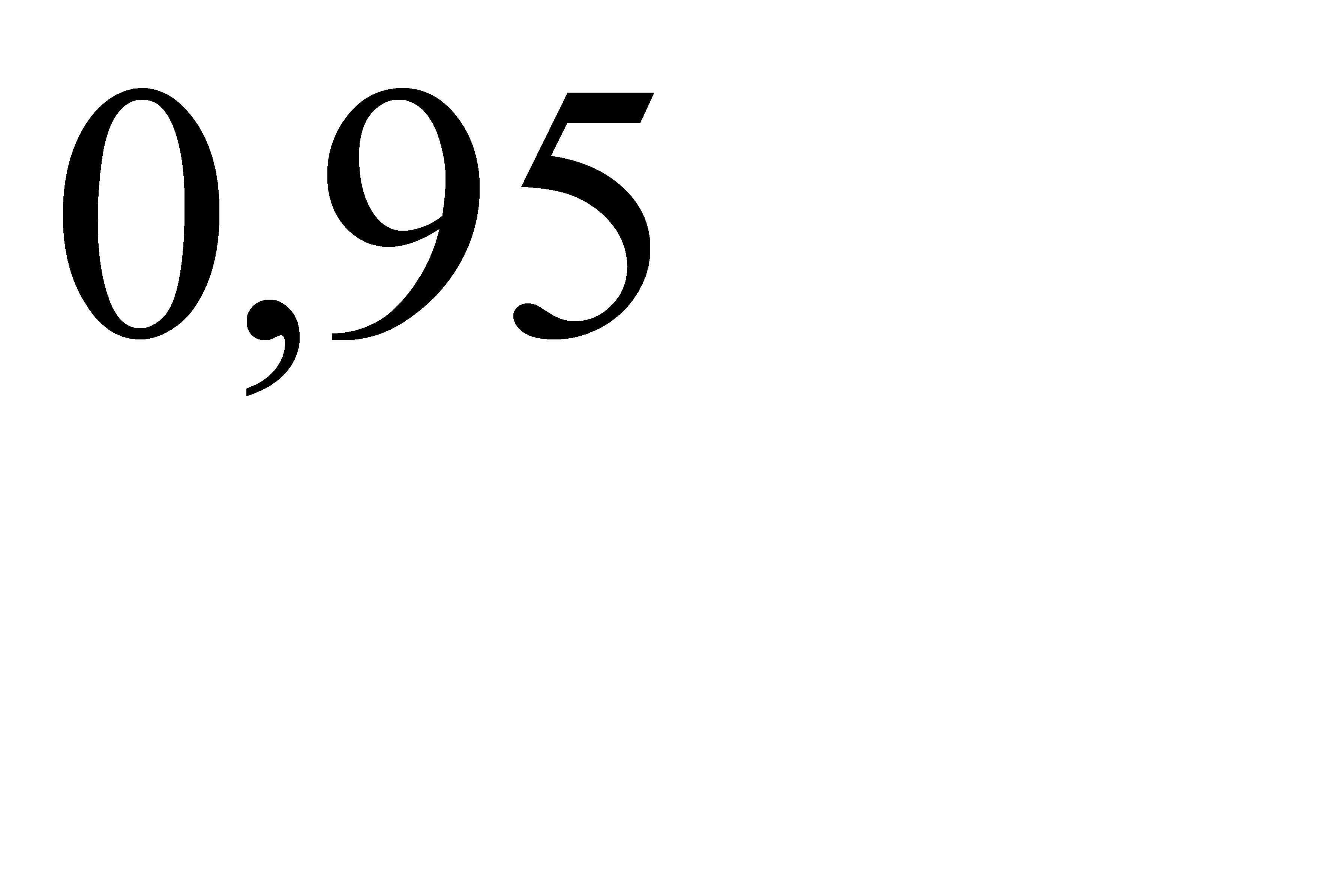 , т.е
, т.е 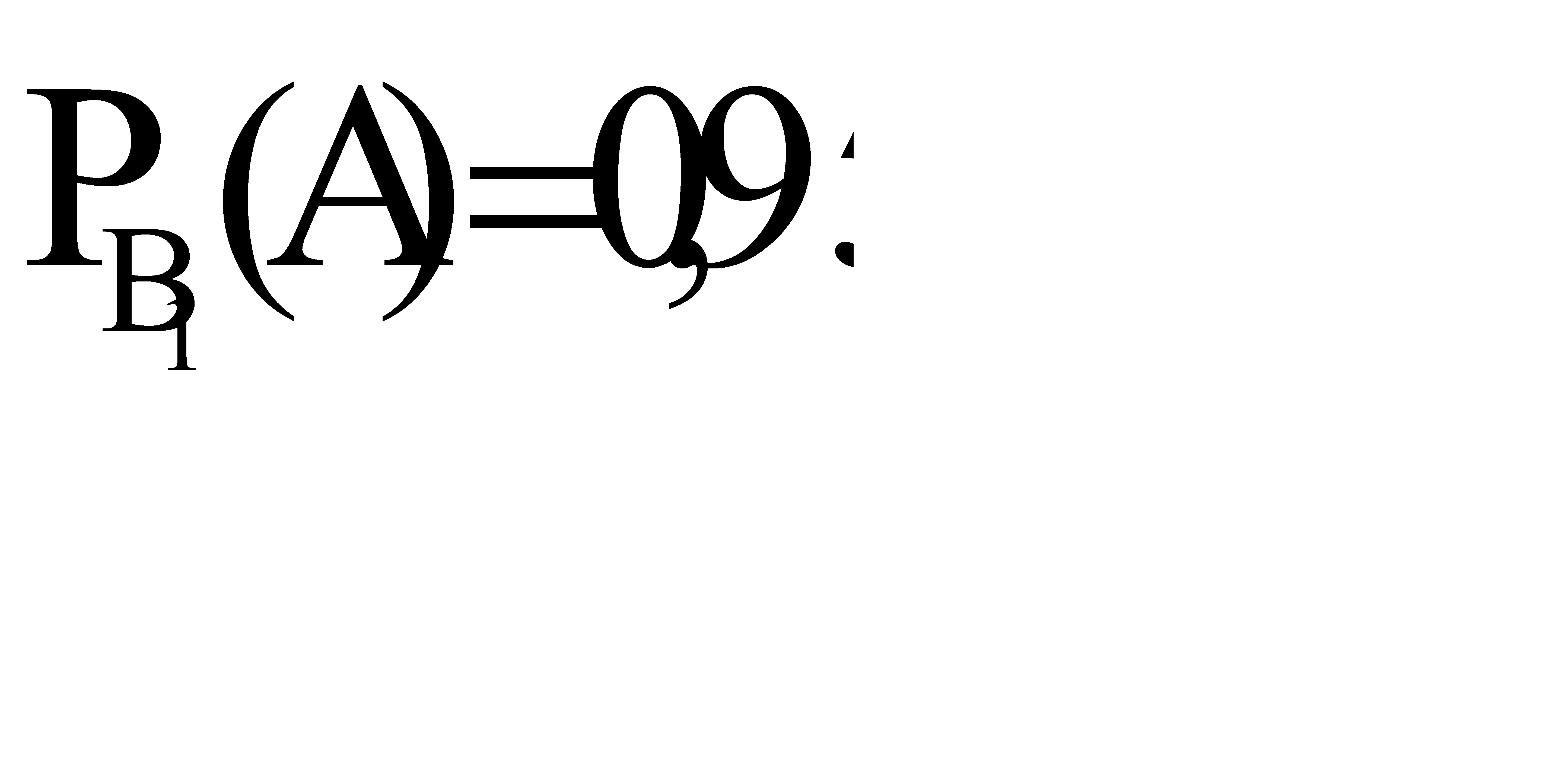 . А условная вероятность того, что полуавтомат не выйдет из строя, равна
. А условная вероятность того, что полуавтомат не выйдет из строя, равна 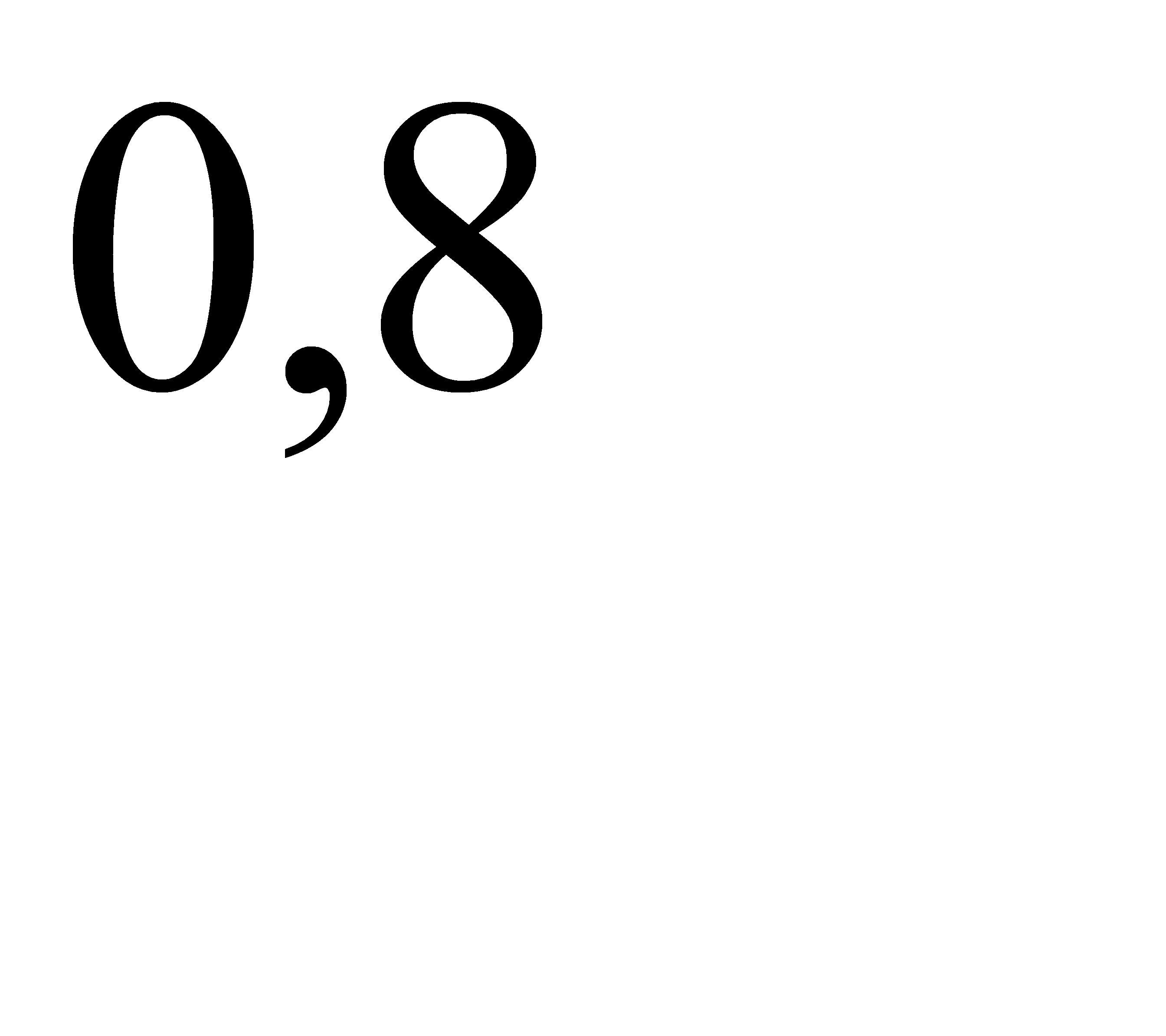 , т.е
, т.е 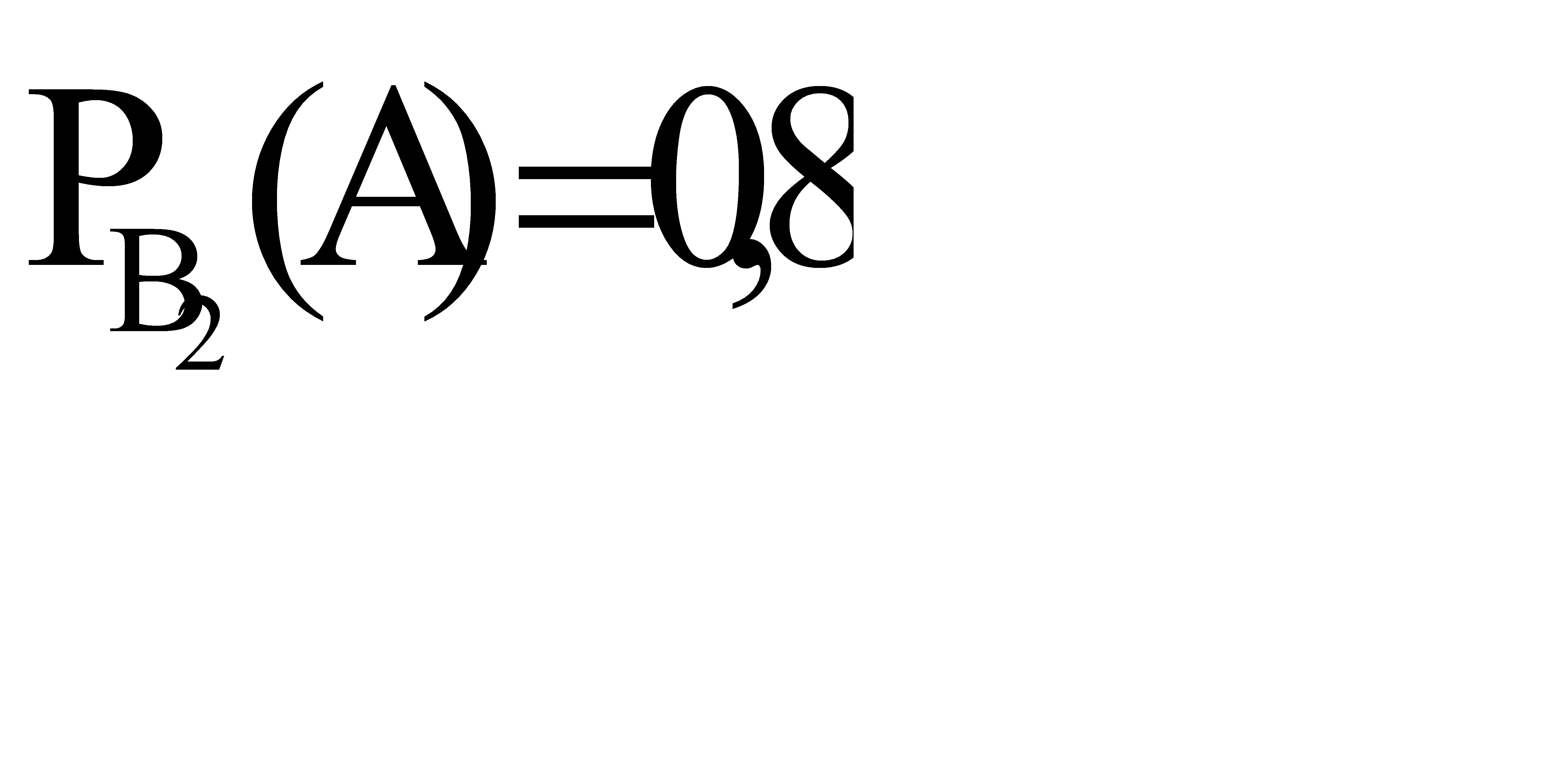 .
.
Искомая вероятность того, что до окончания эксперимента машина не выйдет из строя, находим по формуле полной вероятности:

Ответ: P(A)=0,89
№92 В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.
Решение
Рассмотрим события:
A – стрелок поразит мишень
В1 – взятая наудачу винтовка снабжена оптическим прицелом
В2 – взятая наудачу винтовка без оптического прицела
Следовательно, по условию, вероятность события А при условии события В1: 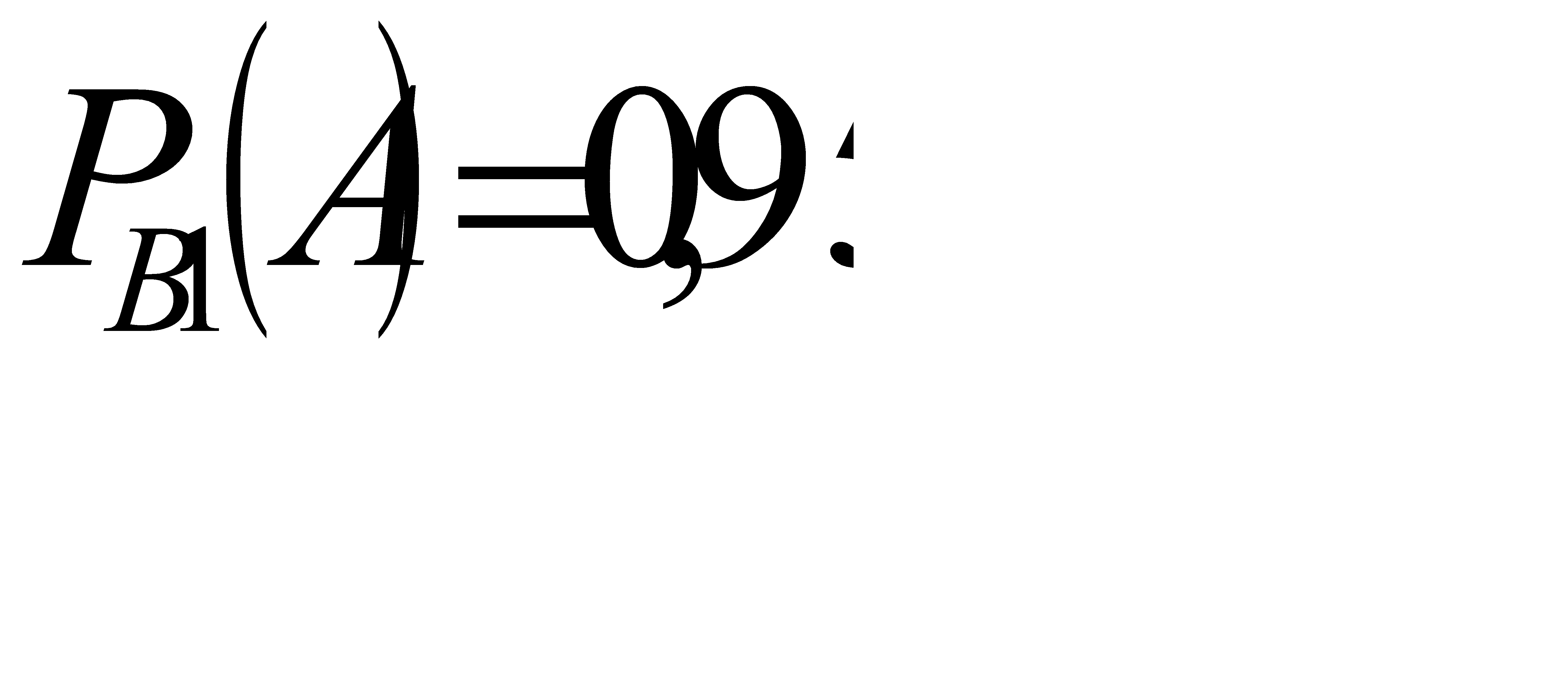 , а вероятность события А при условии события В2:
, а вероятность события А при условии события В2: 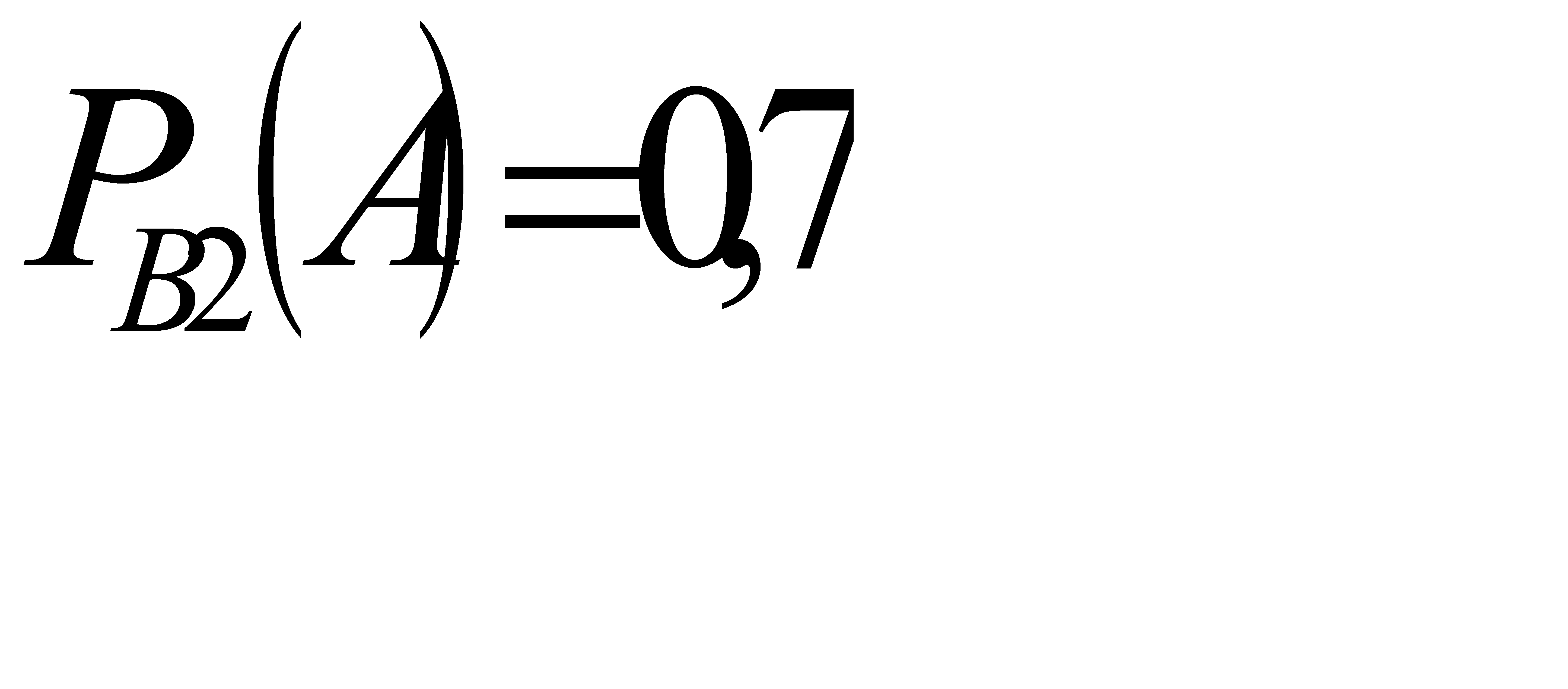 .
.
В свою очередь вероятность события В1: 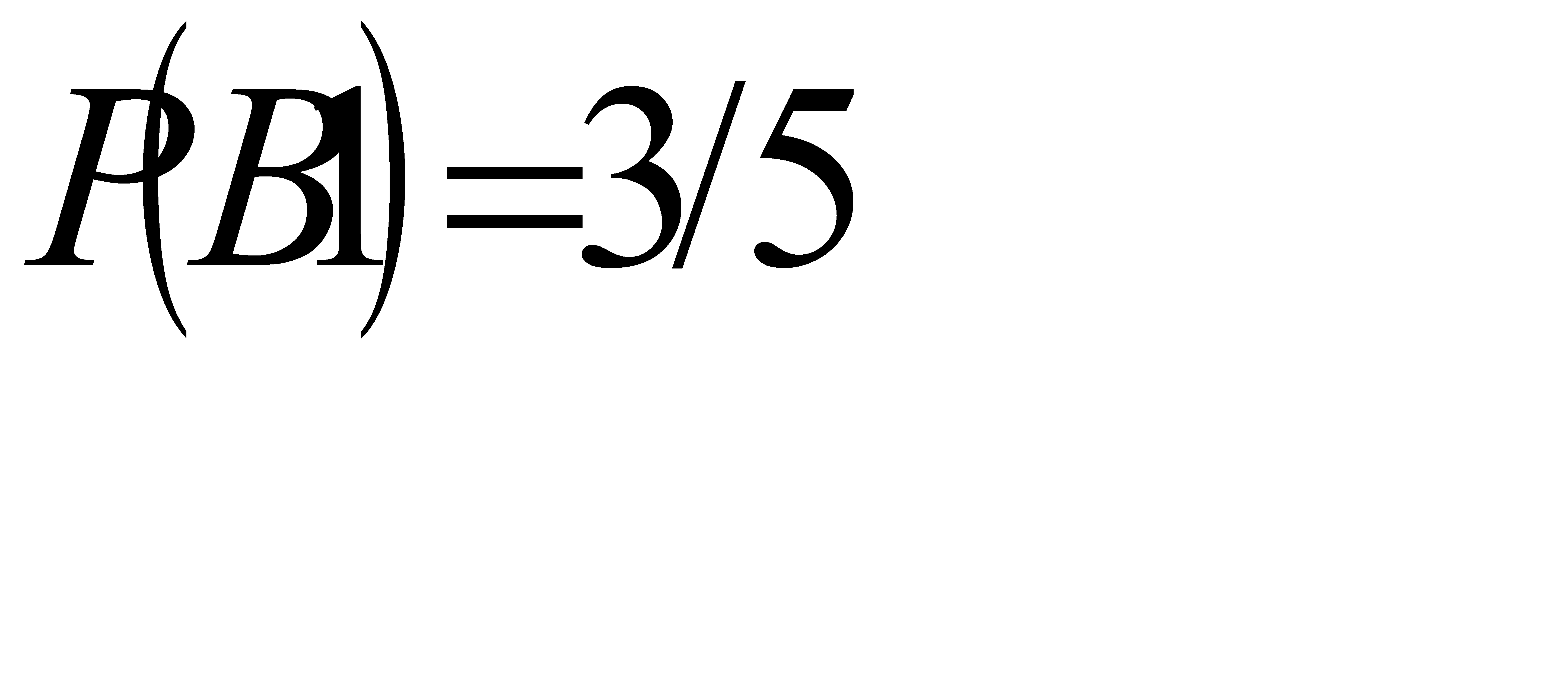 , т.к. всего винтовок 5, а благоприятствуют событию 3 винтовки. Аналогично
, т.к. всего винтовок 5, а благоприятствуют событию 3 винтовки. Аналогично 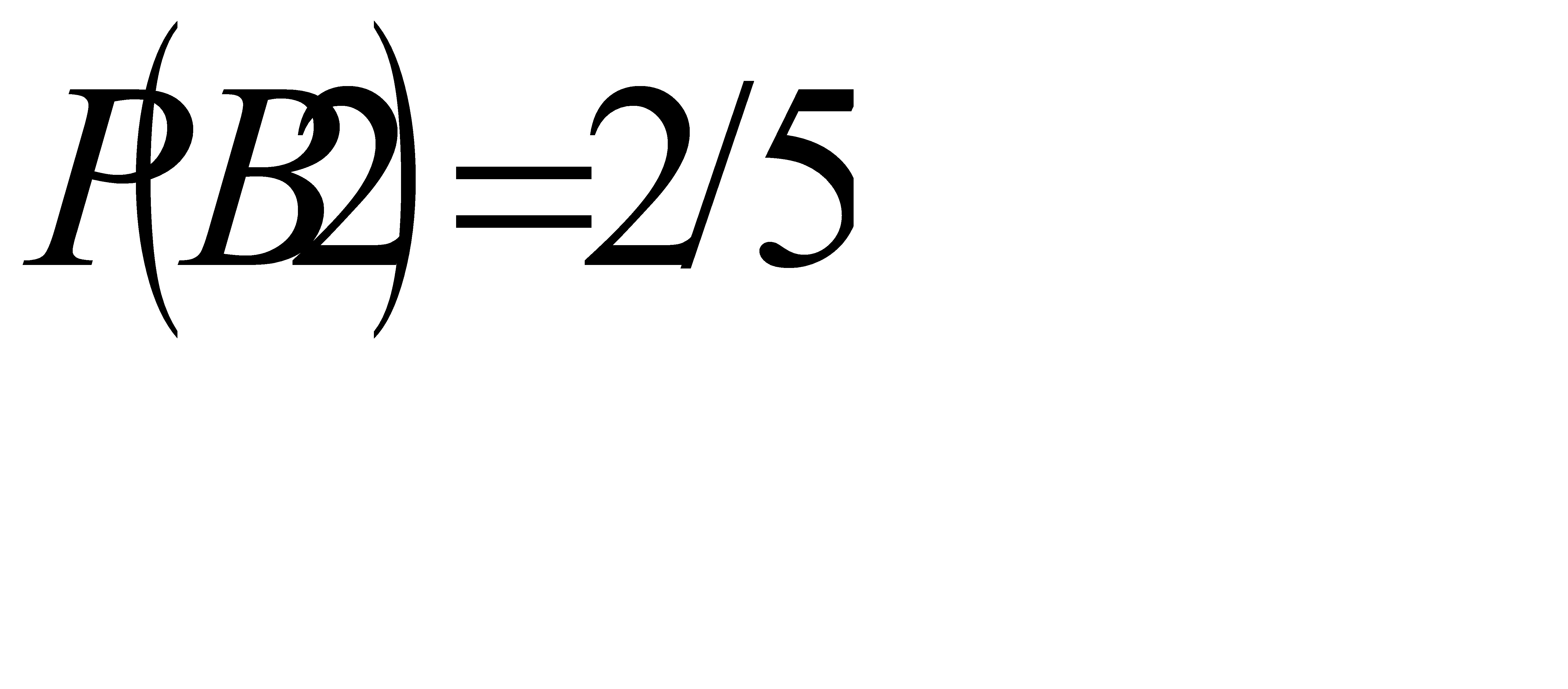 .
.
Пользуясь формулой полной вероятности 
 , получим:
, получим:
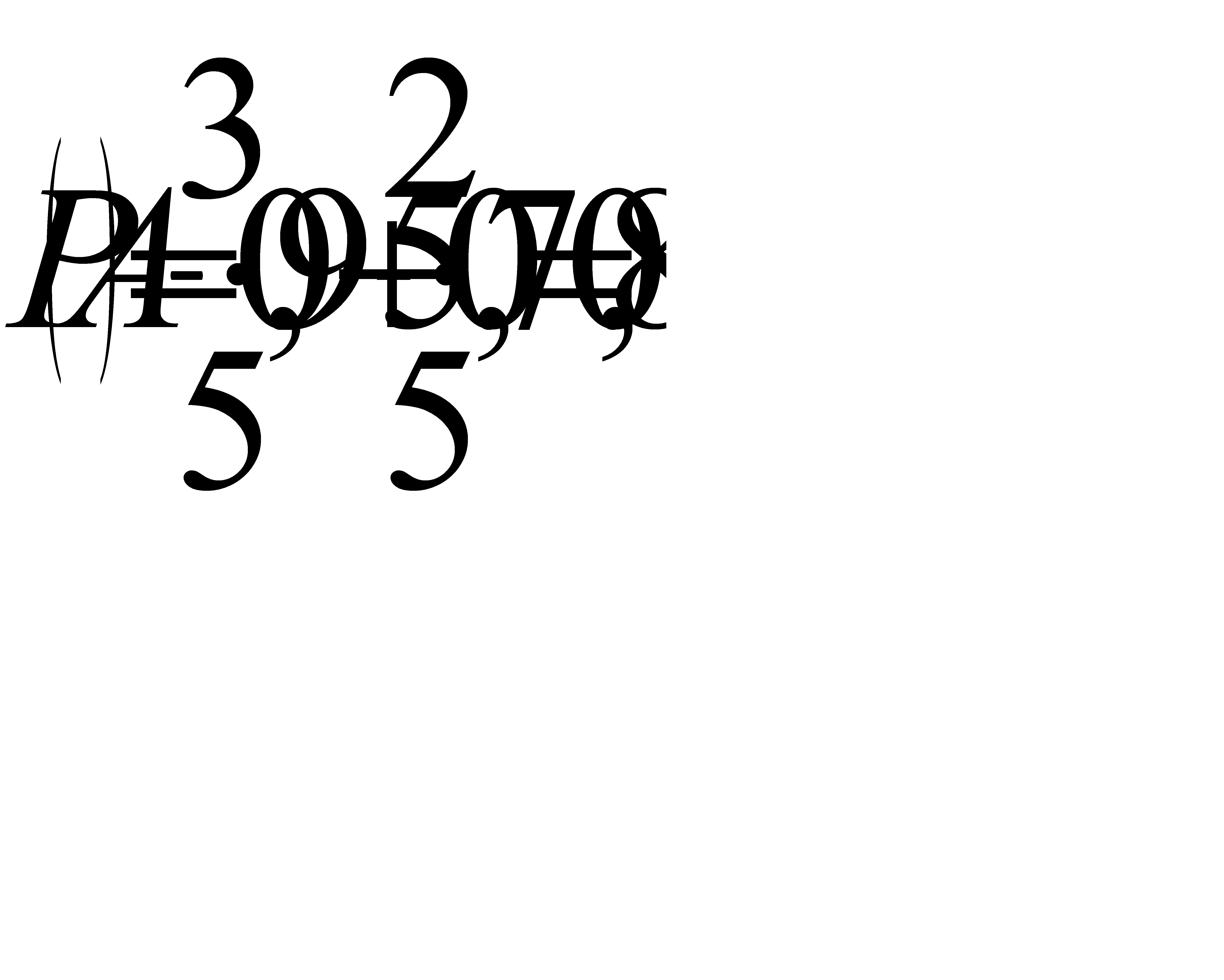
Ответ: 0,85
№93 В ящике содержится 12 деталей, изготовленных на заводе № 1, 20 деталей —на заводе № 2 и 18 деталей— на заводе № 3. Вероятность того, что деталь, изготовленная на заводе № 1, отличного качества, равна 0,9; для деталей, изготовленных на заводах N° 2 и № 3, эти вероятности соответственно равны 0.6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества.
