Домашнее задание 7

7.9. Доказать равенства с помощью геометрических построений:

a) a + 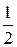(b - a) = 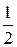(a + b); б) a - 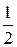( a + b) = 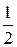(a - b).

7.10. и - медианы треугольника ABC. Доказать равенство .

7.11. M - точка пересечения медиан треугольника ABC, O - произвольная точка пространства. Доказать равенство .

7.12.Точки E и F - середины сторон AD и BC четырехугольника ABCD. Доказать, что . Вывести отсюда теорему о средней линии трапеции.

7.13.Даны два неколлинеарных вектора m и n. Составлены линейные комбинации этих векторов: a = 2m - 3n, b = 3m + n, c = 6m + 2n. Будут ли линейно зависимы следующие пары векторов: а) a и b, б) a и c, в) b и c.

7.14.Будут ли линейно зависимы векторы l, m, n, разложенные по трем некомпланарным векторам a, b, c: l = a + b - c, m = b, n = a + 2b - c. В случае утвердительного ответа указать связывающую их линейную зависимость

7.15.Даны три некомпланарных вектора a, b и c. Доказать, что векторы

a + 2b - c, 3a - b + c, - a + 5b - 3c компланарны.

7.16. Даны три некомпланарных вектора a, b и c. Вычислить значения l и m, при которых векторы la + mb + c и a + lb + mc коллинеарны.