Графики тригонометрических функций

Задача 6.1

Исходя из функции 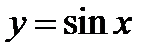, построить график функции .

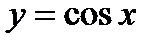Решение.

Функцию 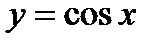представим в виде 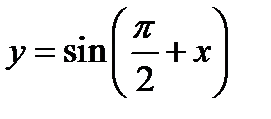. График этой функции получается из графика функции 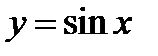(фиг. 6.1), перенесем его вдоль оси 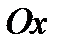влево на 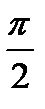ед. масштаба (фиг. 6.2).

Задача 6.2

(для самостоятельного решения). Считая известным график функции 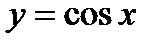(фиг.6.2), построить график функции .

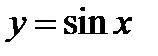Задача 6.3

(для самостоятельного решения). Исходя из графика функции 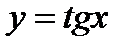построить график функции .

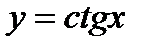Указание. 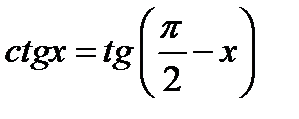. 1) Построить график функции 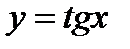(фиг. 6,3):

2)Пользуясь им, получить график функции 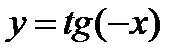и потом с помощью сдвига вдоль оси 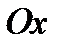получить график функции .

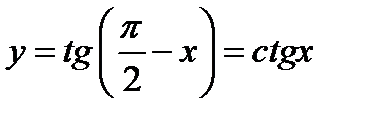График функции 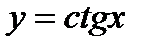представлен на фиг. 6,4.

Задача 6.4

Исходя из графика функции 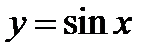, построить график функции .

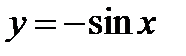Решение.

Если построить кривую, симметричную относительно оси 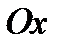графику функции 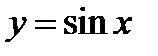, то она и будет являться графиком функции 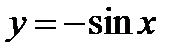(фиг.6.5). График функции 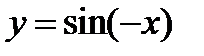совпадает с графиком функции 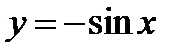. Почему?

Задача 6.5

(для самостоятельного решения). Начертить график функции 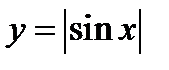(фиг. 6,6).

Задача 6.6

Начертить график функции 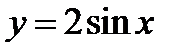, исходя из графика функции .

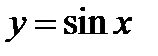Решение.

Начертим одну волну графика функции 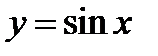на отрезке 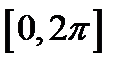(график этой функции можно срисовать из учебника). Выбираем на этом графике несколько точек. Построим теперь на том же чертеже с абсциссами, равными абсциссам выбранных точек, но с ординатами, увеличенными в 2 раза. Соединив эти точки плавной кривой линией, получим приближенный график функции 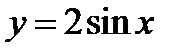(фиг. 6.7).

Теперь пользуясь периодичностью этой функции (ее период равен 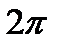), продолжим построенный график в соседние интервалы.

Задача 6.7

(для самостоятельного решения). Построить графики функций:

1) ;

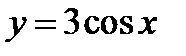2) .

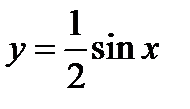Задача 6.8

Построить график функции 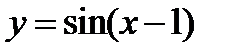, исходя из графика функции .

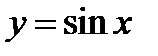Решение.

Чтобы построить график функции 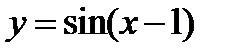, начертим сначала одну волну графика функции 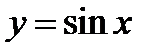на отрезке 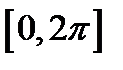и перенесем ее влево на 1 ед. масштаба. Зная, что заданная функция имеет период 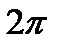, продолжим построенный график в соседние интервалы (фиг.6.8).

Задача 6.9

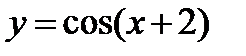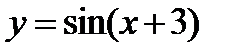(для самостоятельного решения). Построить графики функций: 1) и 2) , исходя из графиков функци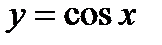й и .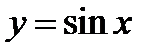

Задача 6.10

Построить график функции .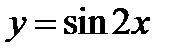

Решение.

Используем указание 4.6 стр.232. Чтобы построить график функции 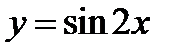, построим одну волну синусоиды 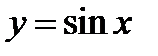на отрезке .

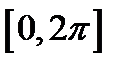Выберем на построенной кривой несколько точек и построим точки с ординатами выбранных точек, но с абсциссами, уменьшенными в два раза. Пользуясь периодичностью заданной функции 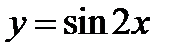(фиг.6.9) (ее период 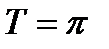) продолжим полученный график в соседние интервалы 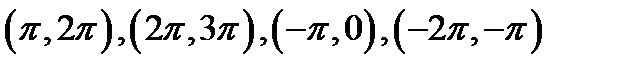, находящееся справа и слева от интервала .

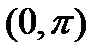Задача 6.11

(для самостоятельного решения). Исходя из графиков функци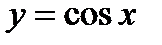й и 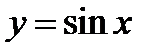, построить графики функций:

1) ;

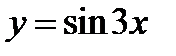2) .

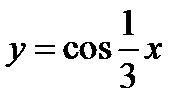Задача 6.12

Построить график функции .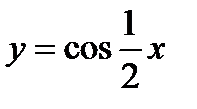

Решение.

Построим на отрезке 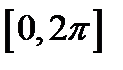сначала график функции 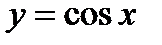(фиг.6.10). Используем указание 4.6 стр.232. Выберем на этом графике несколько точек и построим точки с ординатами, равными ординатами выбранных точек, но с абсциссами, в два раза большими, чем абсциссы выбранных точек.

Построение кривой показано на фиг.6.10. Функция 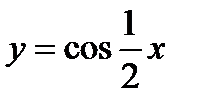—периодическая. Ее период равен 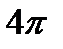. Пользуясь периодичностью этой функции, ее график, построенный на отрезке 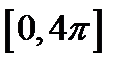, положим в соседние интервалы .

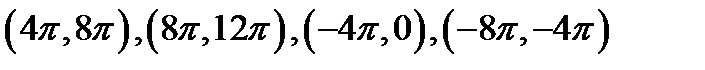Задача 6.13

(для самостоятельного решения). Построить графики функций:

1) ;

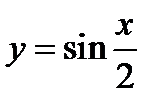2) ;

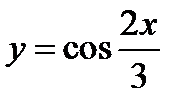3) .

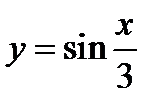Задача 6.14

Построить график функции .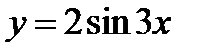

Решение.

Будем исходить из графика функции 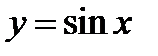. Построим одну волну этого графика на отрезке 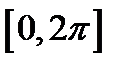. Пользуясь этим графиком, построим график функции 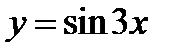. Для этого, как уже известно читателю, следует на кривой 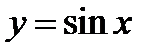выбрать несколько точек и построить точки с ординатами, равными ординатам этих точек, но с абсциссами в два раза меньшими, чем абсциссы выбранных точек. Построенные точки соединяем плавной кривой линией.

После того как построена кривая 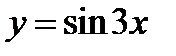, на основании указания 4.5 стр 232 построим кривую 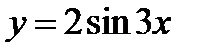, это надо сделать так: оставив абсциссы построенных точек без изменения, построить точки, ординаты которых в два раза больше, чем ординаты построенных точек. Постарения показаны на фиг.6.11. После этого построенную кривую следует продолжить в соседние интервалы 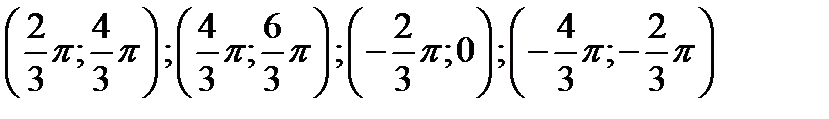и т.д., используя то, что заданная функция – периодическая с периодом .

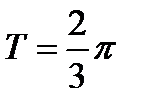Задача 6.15

(для самостоятельного решения). Построить графики функций:

1) ;

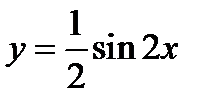2) ;

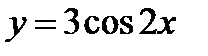3) .

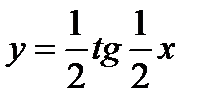Указание. При построении графика функции 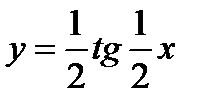следует исходить из графика функции 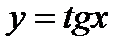. Пользуясь этим графиком, построить график функции 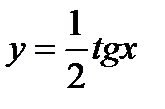, а потом уже кривую .

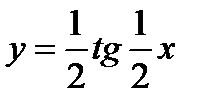Задача 6.16

(для самостоятельного решения). Построить графики функций:

1) ;

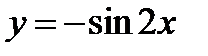2) ;

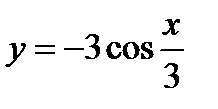3) .

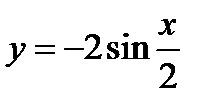Задача 6.17

(для самостоятельного решения). Построить график функции .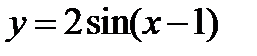

Указание. 1) Исходя из графика функции 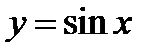построить график функции 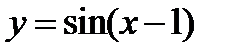. 2) Зная график функции 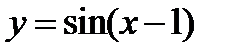, построить график данной функции .

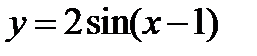Задача 6.18

Построить график функции .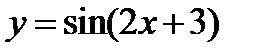

Решение.

Представим заданную функцию в виде 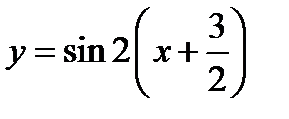и будем вести построение графика в таком порядке:

1) Построим на отрезке 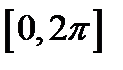график функции .

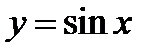2) Выберем на этом графике несколько точек и построим точки с ординатами, равными ординатам выбранных точек, но с абсциссами, уменьшенными в 2 раза. Построенные сочки соединим плавной кривой линией. Эта кривая линия будет графиком функции .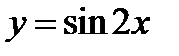

3) Перенесем этот график влево вдоль оси 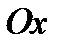на 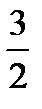ед. масштаба и получим график функции 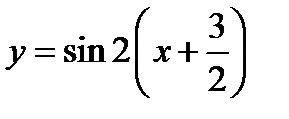, т.е. График заданной функции 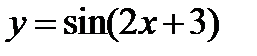(фиг.6.12).

Следует предостеречь читателя от одной распространенной ошибки. Эта ошибка состоит в том, что для построения графика функции 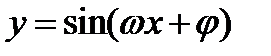иногда поступают так: из графика функции 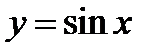получают график функции 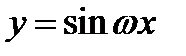, и этот график переносят вдоль оси 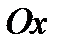на 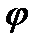ед. масштаба, вместо того, чтобы перенести на 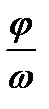ед. масштаба.

Чтобы избежать этой ошибки, надо функцию вида 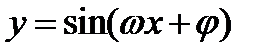представить в виде 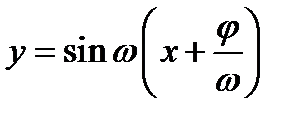, т.е. сделать так, чтобы в скобках под знаком синуса коэффициент при 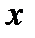был равен 1. Из рассмотрения функции 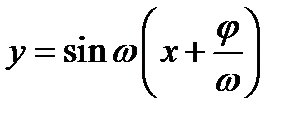сразу видно, что перенос вдоль оси 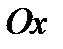должен быть сделан не на 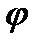ед. масштаба, а на 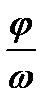ед. масштаба.

Задача 6.19

(для самостоятельного решения). Построить графики функций:

1) ;

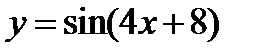2) ;

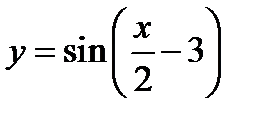3) .

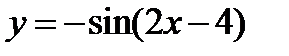Задача 6.20

Построить график функции .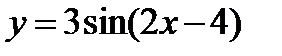

Решение.

Представим заданную функцию в виде 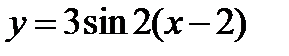. Построим одну волну синусоиды на отрезке 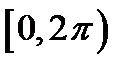.Считая этот график исходным построим график функции .

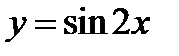Если перенести эту кривую вдоль оси 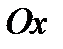на 2 ед. масштаба вправо, то получим график функции 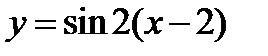. Выберем на этом графике несколько точек и, не изменяя абсцисс этих точек, увеличим их ординаты в три раза. Соединив полученные точки плавной кривой линией, получим приближенный график данной функции 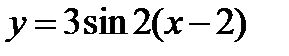. Зная, что заданная функция периодическая и что ее период 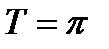, предложим полученный график в соседние интервалы, как мы это делали в предыдущих задачах (фиг. 6.13а).

Задача 6.21

(для самостоятельного решения). Построить графики функций:

1) ;

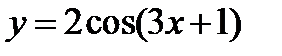2)

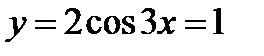
3) ;

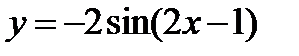4) ;

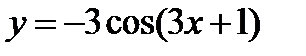5) .

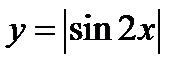Задача 6.22

Построить график функции 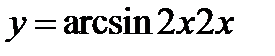, считая исходным график функции .

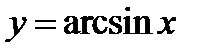Решение.

График функции 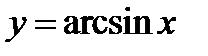представлен на фиг.6.13, перечертите этот график. Выберите на нем несколько точек.

Постройте точки с ординатами, равными ординатам выбранных точек, то с абсциссами, уменьшенными в два раза. Построенные точки соедините плавной кривой линией, которая будет приближенным графиком функции 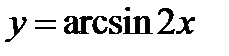(фиг.6.15).

Задача 6.23

(для самостоятельного решения). Пользуясь графиком функции 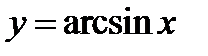(фиг.6.14), постройте графики функций:

1) ;

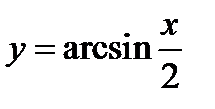2) ;

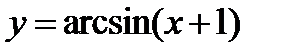3) ;

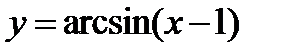4) ;

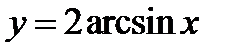5) ;

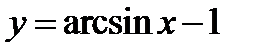6) .

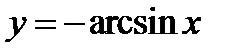Задача 6.24

(для самостоятельного решения). Пользуясь графиком функции 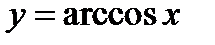(фиг.6.16), построить графики функций:

1) ;

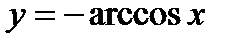2) ;

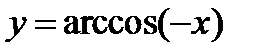3) ;

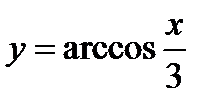4) ;

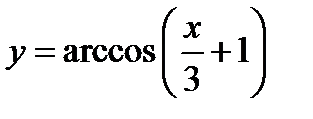5) ;

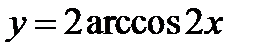Задача 6.25

(для самостоятельного решения). Исходя из графика функци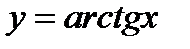и и 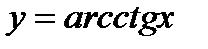(фиг 6.17 и6.18), построить графики функций:

1) ;

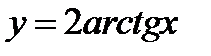2) ;

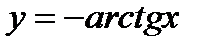3) ;

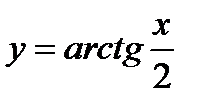4) ;

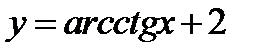5) .

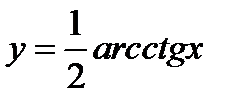СЕДЬМЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ

Содержание: Построение графиков функций, заданных несколькими аналитическими выражениями. Построение графика суммы, разности и произведения нескольких функций.

Определение функции, данное в кратких сведеньях по теории предпосланных второму практическому занятию, не предполагает, что функция обязательно задается по одной формулой. Может оказаться, что на различных участках изменение аргумента функция задана различными формулами.

С таким способом задания функции приходится встречаться и в математических исследованиях, и в таких науках, как сопротивление материалов, теплотехника, радиотехника и др. Поэтому этот способ на следует считать чем-то надуманным.

Задача 7.1

Функция задана следующими равенствами:

Построить график.

Решение.

Если 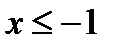, то функция задана равенством 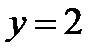и ее графиком будет полупрямая, параллельная оси 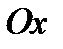(фиг.7.1а). на участке 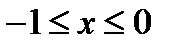функция задана равенством 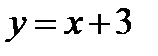. Графиком этой функции является прямая линия, на которой надо взять отрезок ее, соответствующий значениям аргумента 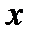из отрезка 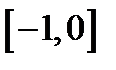(фиг.7.1б).

На участке 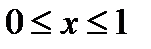функция 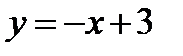, ее график – прямая линия, на которой следует взять отрезок, соответствующий значениям аргумента из отрезка 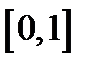(фиг.7.1в) и для значений 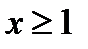функция 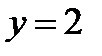и ее графиком будет полупрямая, параллельная оси 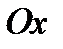(фиг.7.1г).

В «собранном» виде график заданной функции представлен на фиг.7.1 д.

Задача 7.2

Построить график функции, определенной равенствами

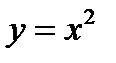, если ;

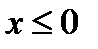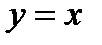, если .

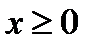Решение.

Графиком функции 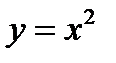для значений 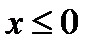является часть параболы, расположенная во втором квадрате (фиг.7.2а).

Графиком функции для значений 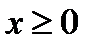является полупрямая – биссектриса первого координатного угла (фиг.7.2б). На фиг.7.2в график заданной функции представлен а «собранном» виде.

Перед решением приведенных ниже задач введем такое условие: если на кривых линиях или на полупрямых поставлены стрелки, то это означает, что концы этих линий, на которых находятся стрелки, не принадлежат графику функций.

Задача 7.3

Построить график функции

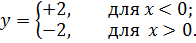
Решение.

См. фиг.7.3

Задача 7.4

(для самостоятельного решения). Построить график функции, определяемой равенствами

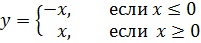
(график этой функции представлен на фиг.7.4). Эта функция может быть задана одним аналитическим выражением: 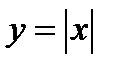, где 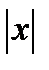—абсолютная величина .

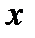Задача 7.5

Построить график функции

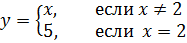
Решение.

График функции состоит из всех точек прямой 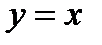, кроме точки (2,2). Эта точка удалена из прямой («изъята». «вырвана»). Она помещена в точку (2,5). Это изолированная точка графика функции (фиг.7.5).

Задача 7.6

(для самостоятельного решения). Построить графики функций, определяемые равенствами:

1)

2)

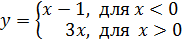
(не забывайте на прямых проставлять стрелки, если они нужны на основании сделанного выше условия. В примере 2) они нужны).

3)

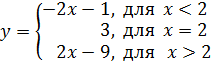
4)

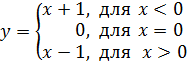
Задача 7.7

(для самостоятельного решения). Построить графики функций, определяемые равенствами:

1)

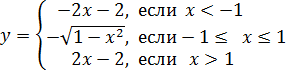
Указание. График функции 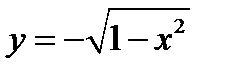— часть окружности 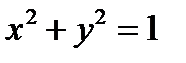, лежащая в нижней полуплоскости (фиг.7.6).

2)

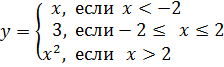
3)

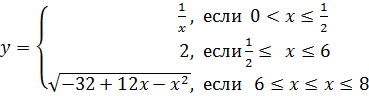
Задача 7.8

(для самостоятельного решения).Построить графики функций:

1) ;

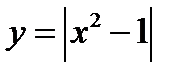2) ;

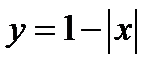3) .

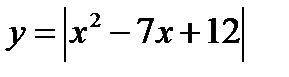Задача 7.9

Построить график функции .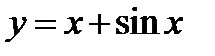

Решение.

Построим на одном чертеже графики слагаемых функций (фиг.7.8): 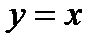и .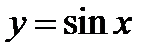

Проведем ряд вертикальных прямых, пересекающих графики этих функций, и пометим на них точки, ординаты которых равны сумме ординат слагаемых функций. Каждая из точек, Построенных на этих вертикальных прямых, имеет абсциссу такую же, как и соответствующие точки обоих графиков. Соединяя полученные точки плавной кривой, получим график данной функции 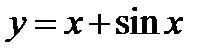(конечно, полученный график будет приближенным).

Задача 7.10

(для самостоятельного решения). Построить графики функций:

1) ;

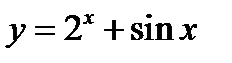2) ;

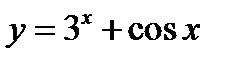3) ;

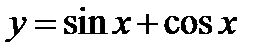4) ;

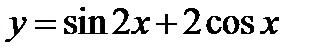5) .

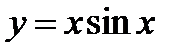Указание. При построении графика функции 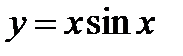(пример5) учесть, что: 1) эта функция четная, а поэтому ее график симметричен относительно оси 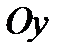. 2) Учитывая, что 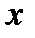умножается на 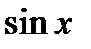, который по абсолютной величине не больше единицы, заключаем, что абсолютная величина произведения 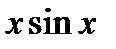, т.е. 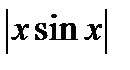, не больше 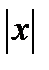, т.е. 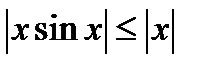, а поэтому график функции 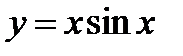расположен между двумя биссектрисами координат углов 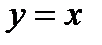и 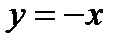. В точках 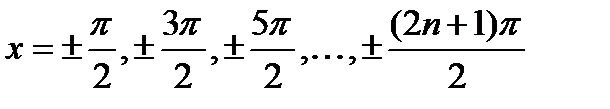график функции 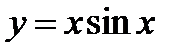касается этих биссектрис, а в точках 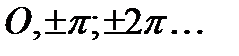, график пересекает ось .

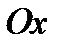Задача 7.11

(для самостоятельного решения). Построить графики функций:

1) ;

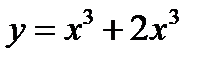2) ;

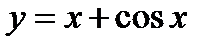3) ;

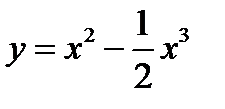4) ;

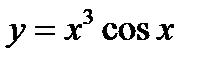5)

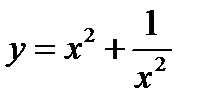
ВОСЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ

Содержание: Решение уравнений с помощью графиков (графическое решение уравнений).

Если не требуется большой точности, то можно корни различных уравнений находить при помощи графиков функций. Для этого поступают так:

Способ 1. Все члены уравнения переносят в его левую часть (первая часть оказывается при этом равной нулю), обозначают левую часть через 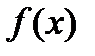, и тогда уравнение приобретет вид 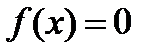. Поле этого строят график функции 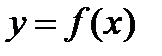, где 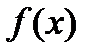—левая часть уравнения. Абсциссы точек пересечения этого графика с осью 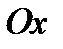и будут корнями уравнения, так как в этих точках .

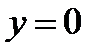Способ 2. Члены уравнения разбивают на две группы, одну из них записывают в левой части уравнения, а другую – в правой. Уравнение приобретает вид 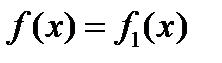. После этого строят графики двух функци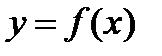й и 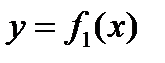. Корнями данного уравнения будут абсциссы точек пересечения этих графиков. Так, если точка пересечения графиков имеет абсциссу 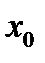, то в этой точке ординаты графиков между собой равны, и тогда 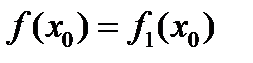. Это равенство показывает, что 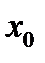—корень уравнения. Второй из указанных способов предпочтительнее первого; он особенно удобен, когда одна из частей уравнения является линейной функцией.

Задача 8.1

Решить графически уравнение 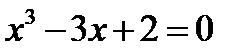первым и вторым из указанных способов.

Решение.

1-й способ. Построим график функции 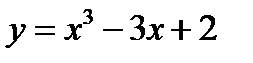(фиг. 8.1) и определим абсциссы точек пересечения этого графика с осью 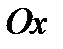: 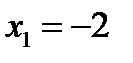; 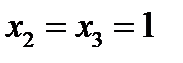. Кривая касается оси 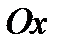в точке 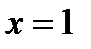, а поэтому уравнение имеет кратный корень 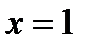(следует иметь в виду, что уравнение третьей степени с действительными коэффициентами имеет или один действительный корень или все три его корня – действительны. Так как кривая пересекла ось в одной точке и коснулась ее в другой, то в той точке, где имеет место касание, будет кратный корень. В данном случае таким двукратным корнем является 1).

2-й способ. Перепишем данное уравнение в виде 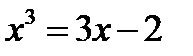. Построим графики функци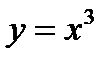й и 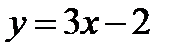(фиг. 8.2). Найдем абсциссы точек пересечения этих графиков. Получим 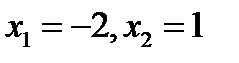. В точке 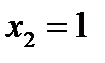прямая 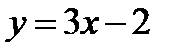касается графика функции .

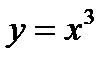Задача 8.2

(для самостоятельного решения). Решить графически уравнение 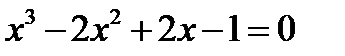. Решить задачу двумя способами.

Ответ.

Один действительный корень .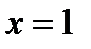

Указание. Прежде чем решить уравнение вторым способом его выгодно сначала упростить. Общий вид кубического уравнения записывается так:

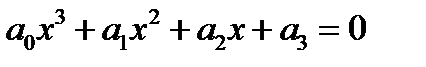(А)

После давления обеих частей равенства на 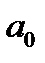оно преобразуется к виду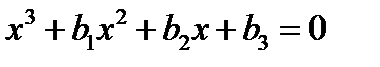

Если теперь сделать подстановку

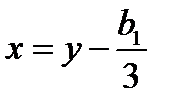(В)

то оно приведется к виду

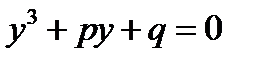(С)

Этот вид кубического уравнения называется приведенным. Оно не содержит квадрата неизвестной величины. Уравнение (С)решить графически проще, чем исходное уравнение (А), т. к. здесь дело сведется к построению графика кубической параболы и прямой (см. предыдущую задачу)., в то время как графическое решение уравнения (А) потребовало бы построения графиков кубической параболы второй степени (уравнение (А) следовало бы переписать так: ).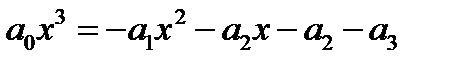

После того как решено уравнение (С), надо воспользоваться подстановкой (В) и найти неизвестное данного уравнения (А).

Задача 8.3

(для самостоятельного решения). Решить графически уравнения:

1) ;

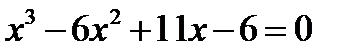2) .

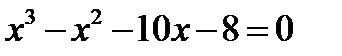Указание. Перейти к приведенному виду (С) кубического уравнения, использовав указание предыдущей задачи.

Ответ.

1) ;

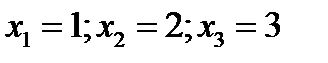2) .

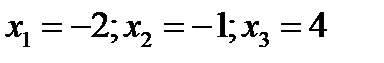Задача 8.4

Найти графически вторы способом положительный корень уравнения .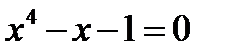

Указание. При построении графиков функци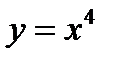й и 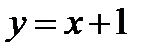масштабную единицу по оси 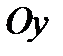уменьшить в 5 раз.

Ответ.

1,22.

Задача8.5

Найти графически наименьший положительный корень уравнения .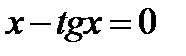

Указание. 1)Переписать уравнение 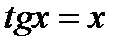; 2)Начертить графики функци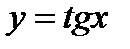й и 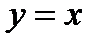. Графики пересекаются в бесконечном множестве точек. Уравнение имеет бесчисленное множество корней.

Ответ.

Наименьший положительный корень 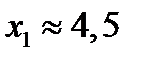(более точное вычисление дает ).

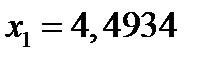Задача 8.6

(для самостоятельного решения).Найти графически наименьший положительный корень уравнения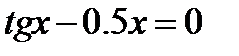

Ответ.

.

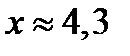Задача 8.7

(для самостоятельного решения). Найти графически наименьший положительный корень уравнения .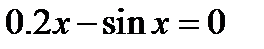

Указание. Искомый корень является наименьшей положительной абсциссой точки пересечения прямой 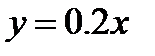и синусоиды .

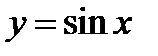Ответ.

.

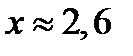Задача 8.8

(для самостоятельного решения). Найти наименьший положительный корень уравнения .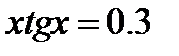

Указание. Переписать уравнение в виде 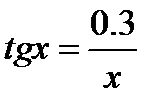и построить графики функци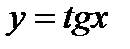й и 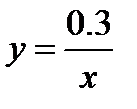(равноосная гипербола).

Ответ.

0,52.

Задача 8.9

(для самостоятельного решения). Найти наименьший положительный корень уравнения .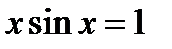

Ответ.

.

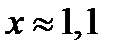Задача 8.10

(для самостоятельного решения). Решить графически уравнения:

1) 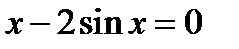(найти положительный корень).

2) .

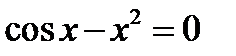Ответ.

1) ;

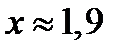2) .

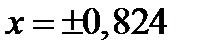ДЕВЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ

Содержание: Обратная функция и ее график. Периодические функции.