Матрицалық теңдеулер

1. AX=XB түріндегі теңдеулер

AX=XB (1)

түріндегі матрицалық теңдеуді қарастырайық, мұндағы A, B берілген квадрат матрицалар (әр түрлі өлшемді), X – ізделінді тік бұрышты матрица: .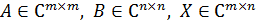

С өрісінде А матрицасының элементар бөлгіштерін:

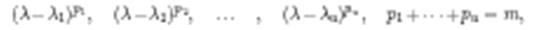
және осы өрісте В матрицасының элементар бөлгіштерін қарастырайық:

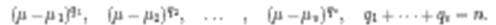
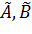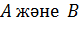деп матрицаларының қалыпты Жордан формасын, ал 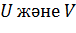деп сәйкес көшу матрицаларын белгілейік:

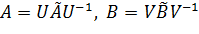(2)

Онда

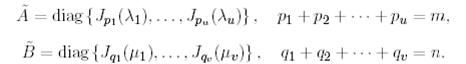
Мұнда

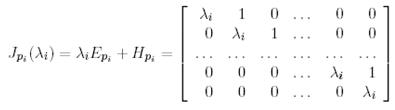
-А матрицасының Жордан торы;

-бірлік матрица;

(3)

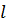- -ші ретті нильпотентті Жордан торы.

(1) теңдіктегі 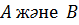матрицаларының орнына (2) өрнекті қойсақ, мынаны аламыз:

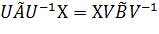(4)

(4)-ші теңдіктің екі жағында сол жағынан 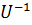-ге, ал оң жағынан 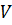-ға көбейтейік:

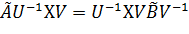(5)

Жаңа белгілеулер еңгізіп:

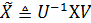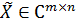, (6)

(5)-ші теңдеуді былай жазайық:

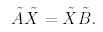(7)

Егер біз (7) теңдеуді 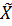-қа қатысты шеше алатын болсақ, онда (1) теңдеудің де шешімі -ке қатысты оңай табылады, себебі (6)-дан

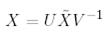(8)

болатындығы шығады.

Ізделінді 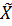матрицасының құрылымын зерттейік. 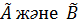матрицаларының блокты – диагоналды түріне сәйкес 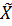матрицасы блоктарға бөлінеді:

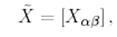
мұндағы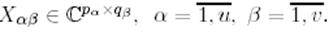

Блокты-диагональды матрицаларға көбейту ережесін қолданып, (7) көбейтуді орындайық:

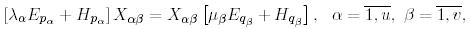
ал бұл мынаған тепе-тең:

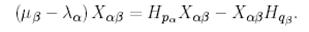(9)

(9) теңдеудің әр қайсысы үшін төмендегі екі жағдайдың бірі орындалуы мүмкін.

1.

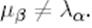
Теңдіктің екі жағын 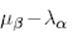көбейтіп және (9)-ға сәйкес 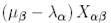-ны 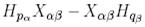-мен алмастырып мынаны аламыз:

.

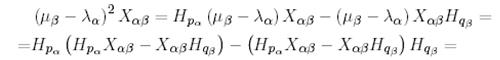
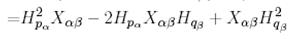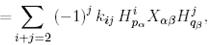
мұндағы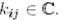

Осы амалды 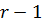рет қайталап, мынаны аламыз:

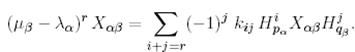(10)

Мынаны ескерейік:

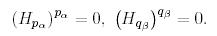(11)

Егер 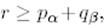болса, онда

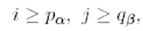
қатынастарының ең болмағанда біреуі орындалады, сондықтан да (11) теңдіктің негізінде 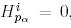не , не 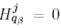және (10) теңдік мына түрге ие болады:

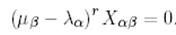(12)

Қарастырылып отырған жағдайда 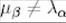болғандықтан, онда (11) теңдіктен

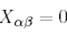(13)

болатындығы шығады.

2.

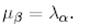
Бұл жағдайда (9) теңдеу мына түрге ие болады:

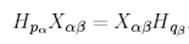(14)

Мұндағы 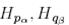матрицалары арнайы құрылымға ие болады: яғни, бірінші диагональ астындағы элементтер бірге, ал қалғандары нөлге тең. Осыны ескере отырып, 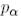және 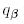мәндеріне сәйкес мынаны аламыз:

2.1. 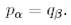Онда

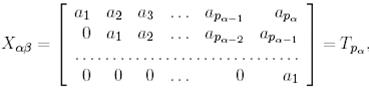(15)

Яғни теңдеудің шешімі квадрат матрица болады, оның бас диагональінің астындағы барлық элементтер нөлге, бас диагональінің элементтері – қандай да бір 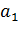параметріне, бірінші диагональ астындағы элементтер – қандай да бір 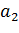параметріне және т.с.с. тең болады.

2.2. 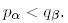Онда

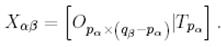(16)

2.3. 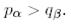Бұл жағдайда

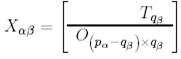(17)

(15)-(17) матрицалары дұрыс жоғары үшбұрышты формаға ие болады деп атайды. Олардағы кез келген параметрлердің саны 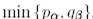тең.

Мысал 1. (Дұрыс жоғары үшбұрышты формадағы матрица).

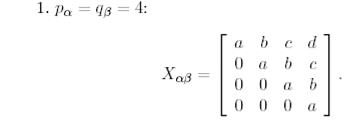
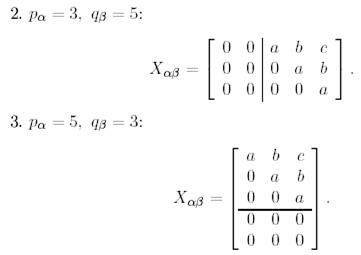
Сонымен, (14) теңдеудің шешімі ретінде кез келген дұрыс жоғары үшбұрышты матрицаны аламыз.

Мынадай белгілеу еңгізейік:

,

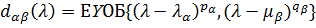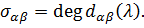
Мұндағы

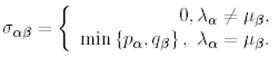
Ендеше 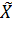-ғы кез келген параметрлер саны (онда 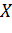-ғы да)

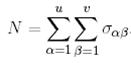
тең.

(7) теңдеудің шешімін 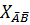деп белгілейік. Онда алынған нәтижені былай тұжырымдауға болады.

Теорема 1. AX=XB (1) , мұндағы

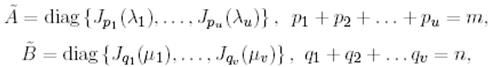
түріндегі теңдеудің жалпы шешімі 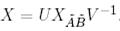формуласымен табылуы мүмкін.

Мұндағы –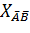

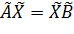
теңдеуінің жалпы шешімі

.

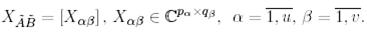Егер 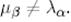болса, онда 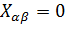болады, егер 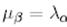болса, онда 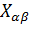- кез келген дұрыс жоғары үшбұрышты матрица болады.

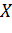матрицасы N кез келген 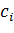параметрлеріне тәуелді:

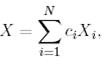
мұндағы

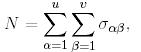
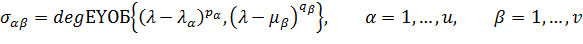
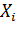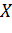- -теналынады, егер 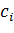параметріне 1 мәнін , ал қалғандарына нөл мәнін берсек, онда ол (1) теңдеудің дербес шешімі болады. Нөлдік емес 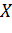шешімі үшін 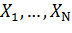дербес шешімдері сызықтық тәуелсіз болады және фундаментальді шешімдер жүйесін құрады. Расында да, егер бұлай болмаса, онда тривиалды емес, яғни 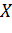матрицасының қандай да бір 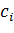параметрінің нөлдік емес мәнінде, 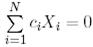сызықтық комбинациясы бар болады, ендеше 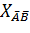нөлге тең болады, ал бұлай болу мүмкін емес.

Салдар 1. Егер 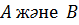матрицаларының меншікті мәндері бірдей болмаса, онда AX=XB (1) теңдеудің тек нөлдік шешімдері ғана боладлы, яғни X=0.

Мысал 2. (AX=XB теңдеуінің шешімі).

Теңдеудің жалпы шешімін табу керек:

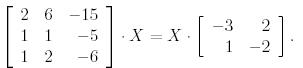
А матрицасы үшін жорданның қалыпты формасын және U көшу(көшіру) матрицасын табайық. Матрицаның сипаттауыш теңдеуі мынаған тең:

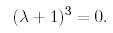
Ендеше, еселігі 3-ке тең жалғыз ғана 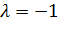меншікті мәні болады.

Меншікті мәнді сипаттауыш матрицаға қояйық:

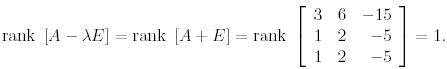
Демек, 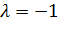меншікті мәніне сәйкес келетін меншікті векторлар кеңістігінің базисін құрайтын векторлардың саны 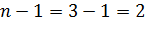тең.

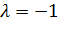меншікті мәніне сәйкес келетін меншікті векторлар кеңістігі мына түрге ие болады:

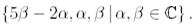
Меншікті векторға қосылған вектор болатындай шартты іздейік:

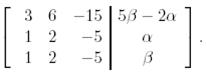
Бұдан, егер 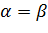болса, онда жүйенің шешімі болады.

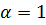деп алайық, онда меншікті вектор 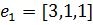болады, ал оған қосылған вектор ретінде 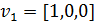векторын, екінші меншікті вектор ретінде 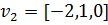векторын аламыз. Осылайша жордан базисін аламыз:

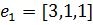
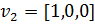
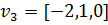
Бұдан

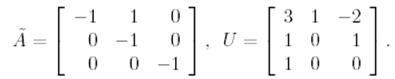
А матрицасының элементар бөлгіштер жүйесі: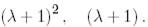

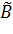және табамыз:

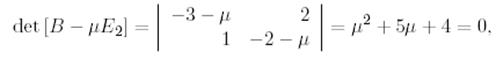
Бұдан .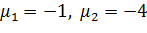

Демек

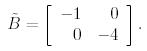
Жордан базисі ретінде 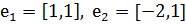меншікті векторларын алуға болады.

В матрицасының элементар бөлгіштер жүйесі:

,

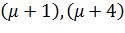жорданның қалыпты формасына көшу матрицасы

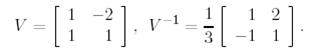
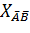табайық:

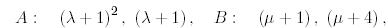
бұдан,

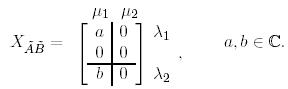
Енді 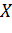-ті табатын болсақ:

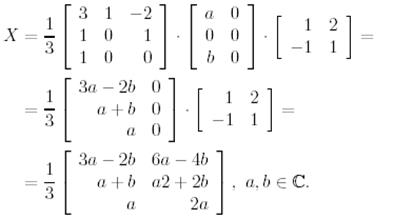(18)