Тәжірибелік сабақ. Математикалық анализге кіріспе. Функция шегі

Тапсырмалар.1. АЖ: [7] № 1.106, 1.206, 1.172, 1.280, 1.288, 1.306, 1.314, 1.320, 1.322

2. ҮЖ: [7] № 1.109, 1.233, 1.273, 1.277, 1.289, 1.297, 1.305, 1.307, 1.327.

Әдістемелік ұсыныстар.

Функция шегі туралы теоремалардың ең болмағанда бір шарты орындалмаса, онда 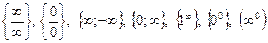және т.б. түрдегі анықталмаған өрнектер пайда болады. Мұндай өрнектердің шегін табу анықталмағандықтарды шешу деп аталады. Ол үшін анықталмаған өрнектерге түрлендірулер жасау, тамаша шектерді қолдану қажет.

1. Егер 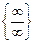анықталмағандығы екі көпмүшеліктің қатынасы түрінде берілсе, онда бөлшектің алымын да, бөлімін де өрнектегі айнымалы шаманың ең жоғарғы дәрежесіне бөлеміз.

2. Егер 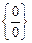анықталмағандығы көпмүшеліктердің қатынасы түрінде берілсе, онда көпмүшеліктерді көбейткіштерге жіктеу қажет. Мысалы, 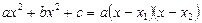, мұндағы, 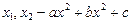теңдеуінің түбірлері.

3. Егер 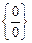анықталмағандығы тригонометриялық функциялар немесе кері тригонометриялық функциялар арқылы берілсе, онда бірінші тамаша шекті пайдаланамыз.

4. 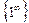- анықталмағандықты шешу үшін екінші тамаша шекті пайдаланамыз.

5. Иррационал өрнектері бар функциялардың шектерін есептеу үшін: а) иррационалдықты алымынан бөліміне көшіру немесе керісінше; б) жаңа айнымалыны енгізу арқылы иррационал өрнекті рационал өрнекке келтіру қолданылады.

1-есеп. Шекті есептеңіз: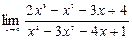

Шешуі. 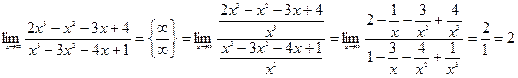, себебі, 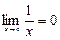, , 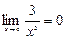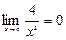және т.с.

2-есеп. Шекті есептеңіз: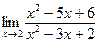

Шешуі.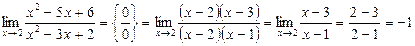

3-есеп. Шекті есептеңіз: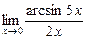

Шешуі. 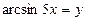десек, онда 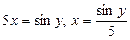. Егер 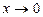, онда .

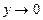Ендеше, .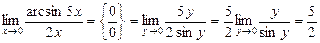

Негізгі әдебиет: [7], 3 тарау, § 3.4-3.4 (128-181 беттер).

Қосымша әдебиет: [18], 1 тарау, § 2 (11-14 беттер), 2 тарау, § 4 (34-39 беттер).

Бақылау сұрақтары:

1. Шектер туралы теоремалар қандай?

2. Тамаша шектер дегеніміз не?

3. Тамаша шектердің қандай салдарлары бар?

Тәжірибелік сабақ. Шексіз аз, шексіз үлкен функциялар. Функция

Зіліссіздігі

Тапсырмалар.1. АЖ: [7] № 1.350, 1.366, 1.368, 1.390,1.398, 1.400.

2. ҮЖ: [7] № 1.351, 1.367, 1.369, 1.387, 1.393, 1.399.

Әдістемелік ұсыныстар.

1. Мәндес шексіз аздарды пайдаланып та шекті есептеуге болады.

2. Функцияның нүктедегі үзіліссіздігі анықтамасы бойынша зерттеледі. Функцияның үзіліс нүктелерін анықтау үшін оның біржақты шектерін есептей білу қажет.

1-есеп. 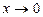болғанда 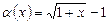, 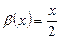функцияларын салыстырыңыз.

Шешуі.

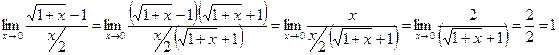. Сондықтан, .

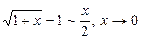2-есеп. Шекті есептеңіз: .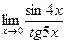

Шешуі. Шекті табу үшін мәндес шексіз аз функцияны пайдаланамыз: 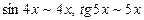, себебі 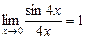, 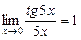. Ендеше, .

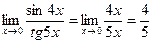3-есеп. Функцияны үзіліссіздікке зерттеңіз: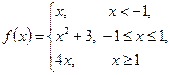

Шешуі. Берілген функция 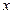-тің барлық мәндерінде анықталған, бірақ ол әрбір аралықта әртүрлі аналитикалық өрнектермен берілген. Бұл аналитикалық өрнектер-элементар функциялар. Сондықтан берілген функция өзінің аналитикалық түрін өзгертетін нүктелерден басқа нүктелерде үзіліссіз. Ендеше, функцияны 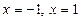нүктелерде үзіліссіздікке зерттейміз.

. , , .

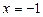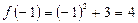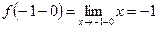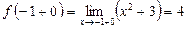Функцияның біржақты шектері бар және олар өзара тең емес болғандықтан, 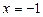нүктесі бірінші текті үзіліс нүктесі болады.

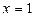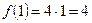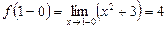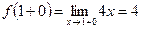. , , . Яғни, 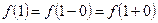, ендеше, 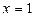нүктесінде функция үзіліссіз. (1-сурет)

Негізгі әдебиет: [7], 3 тарау, § 3.3, 3.5-3.9 (182-210 беттер).

Қосымша әдебиет: [18], 2 тарау, § 3,4 (32-34, 39-43 беттер).

Бақылау сұрақтары:

1. Шексіз аз шамалардың қандай қасиеттерін білесіз?

2. Функцияның біржақты шектері дегеніміз не?

3. Бірінші және екінші текті үзілісті функцияларды қалай ажыратуға болады?