Движение броуновских частиц
Броуновское движение
1827 г. Р. Броун
Энергия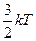 
, приходящаяся на три поступательные степени свободы частицы, приводит к движению ее центра масс, которое и наблюдается под микроскопом в виде дрожания.
Случайные блуждания
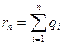, где 
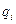- смещение.
.
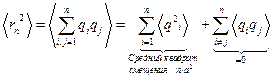Но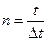 
, и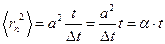 
- средний квадрат удаления зависит от времени линейно.
Пятно из броуновских частиц расползается.
Движение броуновских частиц
Уравнение движения частицы
.
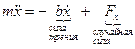Умножим на x
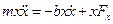
Т.к.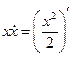 
и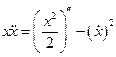 
,
.
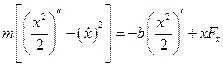Усредним по ансамблю.
Среднее от производной по времени равно производной от средней величины
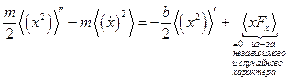
Отклонение частицы в любом направлении равновероятно, т.е.
.
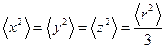Т.е.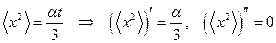 
.
Таким образом, учитывая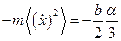 
, 
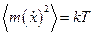, получим
,
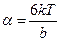где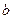 
можно найти из формулы Стокса, т.е. экспериментально.
И так
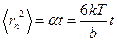
Все величины известны
В 1908 г. Ж.Б. Перрен подтвердил экспериментально эти зависимости.
Известно, что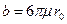 
, где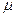 
- вязкость жидкости, 
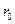- радиус шарообразной частицы.
Тяжелые частицы дрожат менее интенсивно, однако пятна из легких и тяжелых частиц расползаются с одной скоростью.
«Много движений и никаких достижений»