Движение без вращения частиц.

Потенциал скорости

Рассмотрим один частный, но весьма важный случай движения жидкости – движение без вращения частиц. Для удобообтекаемых тел вращение частиц отсутствует почти во всем потоке, за исключением пограничного слоя, областей разрыва скоростей (отрывные зоны, спутнаяструя, скачки уплотнения).

Многие вопросы аэродинамики ЛА решаются в предположении, что обтекание происходит без вращения частиц (вопросы о распределении давления, аэродинамические нагрузки).

Если вращение отсутствует, то 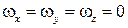, и из формул (2.9) следует, что

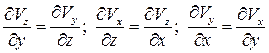. (2.10)

Эти равенства позволяют значительно упростить вычисления , так как задачу об определении поля скоростей можно свести к нахождению лишь одной неизвестной функции. Рассмотрим выражение

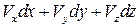. (2.11)

Из математики известно, что если это выражение является полным дифференциалом некоторой функции, то крест-накрест взятые частные производные от коэффициентов 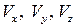должны быть равны между собой. Этому условию как раз и отвечают равенства (2.10). Таким образом, если движение жидкости происходит без вращения частиц, то выражение (2.11) является полным дифференциалом некоторой функции координат.

Обозначив эту функцию через 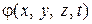(время t здесь является параметром, а не независимой переменной), можем записать

.

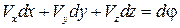С другой стороны, полный дифференциал функции j как функции координат можно записать в виде 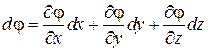. Сравнивая выражения для 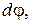можно увидеть, что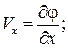 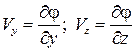, и после подстановки их в равенства (2.10) получаем тождества, подтверждающие, что функция j удовлетворяет названному условию.

Функция j – потенциал скорости (название предложил Гельмгольц). В случае потенциального движения интеграл от дифференциального выражения (2.11) не зависит от формы пути, а зависит только от положения (координат) начальной А и конечной В точек:

.

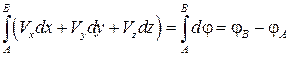Потенциальное движение – безвихревое. Примером потенциального течения может служить фотография обтекания шара при очень малых числах Рейнольдса (рис. 2.5).

Таким образом, проекция вектора скорости V на любое направление S равна производной от потенциала скорости по этому направлению. Запишем выражение для этой проекции через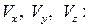

,

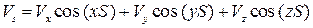где 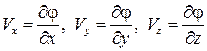, а направляющие косинусы равны 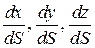. Следовательно, 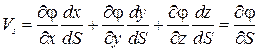и для любого направления

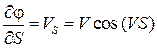. (2.12)

Формула (2.12) выражает свойство потенциала скорости, которое заключается в следующем:

Проекция вектора скорости на любое направление равна частной производной от потенциала скорости по этому направлению.

Определив при решении задачи потенциал j, можно легко определить любые компоненты скорости.

Геометрически j можно представить в виде семейства поверхностей 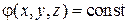. Такие поверхности, в любой точке которых потенциал сохраняет одно постоянное значение, называются поверхностями равного потенциала. Пусть направление S совпадает с касательной в данной точке к поверхности 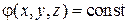. Тогда 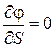, и из формулы (2.12) следует, что 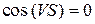, т. е. линии тока ортогональны к поверхностям равного потенциала( ).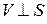