Классификация центральных кривых второго порядка (случай d ¹ 0)

Попробуем дальше упростить уравнение (9). Выберем новую декартову СК O¢x²y², которая получается из O¢x¢y¢ поворотом координатных осей на некоторый угол a . Тогда формулы замены координат имеют вид:

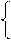
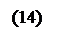x¢ = x²·cos a – y²·sin a,

y¢ = x²·sin a + y²·cos a.

Подставим эти формулы в (9):

а₁₁(x²·cos a – y²·sin a)² + 2а₁₂(x²·cos a – y²·sin a)(x²·sin a + y²·cos a) +

+ а₂₂(x²·sin a + y²·cos a)² + с¢ = 0,

Раскроем скобки и приведем подобные при одинаковых координатах. Тогда коэффициент x²y² будет равен

– а₁₂sin²a + (а₂₂ – а₁₁)sin a·cos a + а₁₂cos²a

Приравняем это выражение к нулю, и получившееся уравнение разделим на – cos²a :

а₁₂ tg²a + (а₁₁ – а₂₂) tg a + а₁₂ = 0. (15)

Это квадратное уравнение относительно неизвестного tg a, его дискриминант

D = (а₁₁ – а₂₂)² + а₁₂ ³ 0.

Значит, (14) всегда имеет решение, т.е всегда существует такой угол a, что в новой СК мы получим уравнение кривой без слагаемого, содержащего x²y². В результате наше уравнение будет иметь вид

l₁(x²)² + l₂(y²)² + = 0. (16)

Примем пока без доказательства, что коэффициенты l₁ и l₂ являются корнями уравнения

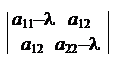= 0 ;

в развернутом виде:

l²– sl + d = 0, (17)

где s = trace A = а₁₁ – а₂₂ – след матрицы A. Оно называется характеристическим уравнением кривой второго порядка. Согласно теореме Виета получаем

l₁+ l₂ = s , l₁·l₂ = d.

Относительно новой СК O¢x²y² получаем

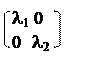
A¢ = , d¢= det A¢= l₁·l₂ = d, s¢= trace A¢ = l₁+l ₂ = s,

l₁ 0 0

D¢ =0 l₂ 0 = l₁·l₂· (D/d) = D .

0 0 D/d

Таким образом, d¢= d , s¢= s, D¢ = D , т.е. величины d , s, D не изменяются при переходе к новой декартовой СК. Поэтому они называются инвариантами кривой второго порядка.

1 случай: D ¹ 0. Если опустить штрихи, то уравнение (16) можно переписать в виде

+ = 1. (18)

Обозначим a² = |D/l₁d|, b² = |D/l₂d|.

а) d > 0, sD < 0. Тогда l₁·l₂> 0 , т.е. l₁ и l ₂ одного знака, и (l₁+ l ₂)·D < 0, т.е. знак D противоположен знаку l₁ и l ₂. Поэтому оба знаменателя в (17) положительны, и уравнение (15) задает эллипс:

+ = 1 .

б) d > 0, sD > 0. Тогда оба знаменателя в (18) отрицательны, и уравнение имеет вид

+ = –1 .

Говорят, что оно задает мнимый эллипс. На действительной плоскости это пустое множество.

в) d < 0, D ¹ 0. Тогда l₁ и l ₂ имеют разные знаки, и поэтому знаменатели в (17) имеют разные знаки. Получаем уравнение

– = 1 или – = –1.

В любом случае получается уравнение гиперболы.

2 случай: D = 0. В этом случае уравнение (15) принимает вид (штрихи опускаем):

l₁x² + l ₂y² = 0. (19)

Обозначим a² =½l₁½, b² =½l₂½.

а) d < 0. Тогда l₁ и l ₂ разного знака и (18) можно переписать в виде

a²x² – b² y² = 0 Û

Û (ax – b y)·(ax + b y) = 0.

Этому уравнению удовлетворяют точки, для которых ax – by = 0 и точки для которых ax + by = 0 . Поэтому оно определяет пару прямых, очевидно, пересекающихся в центре O¢ и симметричных относительно координатных осей.

б) d > 0. Тогда l₁ и l ₂ имеют одинаковые знаки и (19) можно переписать в виде

a²x²+b²y² = 0 Û (ax – i b y)·(ax + i b y) = 0.

(i – мнимая единица). Говорят, что это уравнение задает пару мнимых пересекающихся прямых. Но пересекаются они в действительной точке O¢ – центре кривой.

В случае d = D = 0 кривая тоже имеет центр (бесконечное количество центров), но этот случай мы рассмотрим в следующем параграфе.

§9. Классификация нецентральных кривых второго порядка (случай d = 0).

Пусть теперь d = 0. Тогда мы не можем использовать процедуру нахождения центра, и сразу совершаем поворот координатных осей на угол, тангенс которого находится из уравнения (14). Получим новую декартову СК с тем же началом Ox¢y¢. Формулы замены координат имеют вид

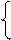x = x¢×cos a – y¢×sin a,

y = x¢×sin a + y¢×cos a.

Здесь на один штрих с каждой стороны меньше, чем в (14), поскольку это первая замена координат. В этой СК уравнение кривой не будет включать слагаемое, содержащее произведение x¢y¢:

l₁x¢² + l ₂ y¢² + 2b₁х¢ + 2b₂ у¢ + с = 0, (20)

Заметим, что коэффициент с останется прежним, а непосредственное вычисление показывает, что

b₁= a₁×cos a + a₂×sin a, b₂ = a₁×sin a + a₂×cos a.

Числа l₁ и l ₂ можно найти из уравнения (17). Так как d = l₁·l₂ = 0, то один из корней будет равен нулю. Пусть это будет l₁. Имеем уравнение

l ₂ y¢² + 2b₁х¢ + 2b₂ у¢ + с = 0. (21)

Для этого уравнения

0 0 b₁

D = 0 l₂ b₂ = – l₂b₁².

b₁ b₂ с

1 случай: D = 0 Û b₁= 0. Уравнение имеет вид l ₂ y¢² + 2b₂ у¢ + с = 0. Выделим полный квадрат:

l ₂( y¢ ² + у¢ + ) – + с = 0 Û l ₂( y¢ + )²– + с = 0 .

Обозначим с¢= (b₁²- l ₂с) /l ₂, a² =½ с¢½ и сделаем замену координат:

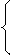x²= x¢ ,

y²= y¢ + ,

которая равносильна переносу начала координат в точку O¢(0,– b₁/l₂)_Ox¢y¢(подчеркнем, что координаты указаны в промежуточной СК Ox¢y¢). Получим уравнение

(y²)² = a².

а) с¢ > 0 Þ (y²)² = a², т.е. y² = a или y² =– a . Наша кривая – это пара параллельных прямых.

б) с¢ > 0 Þ (y²)² =– a², т.е. y² = i a или y² =– i a . Говорят, что наше уравнение задает пару мнимых параллельных прямых.

в) с¢ = 0 Þ (y²)² =0. Говорят, что это уравнение задает пару совпадающих прямых.

2 случай: D ¹ 0 Û b₁¹ 0. Так же, как и в предыдущем случае, выделяем в (21) полный квадрат по y:

l ₂²– + 2b₁х¢ + с = 0 ,

а затем преобразуем так:

l ₂²+ 2b₁ = 0 .

Обозначим c¢ = и сделаем замену координат:

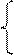x²= х¢ – c¢ ,

y²= y¢ + ,

которая равносильна переносу начала координат в точку O¢_Ox¢y¢. Получим уравнение

l ₂(y²)² + 2b₁х² = 0 Û (y²)² = 2pх²,

где p = – 2b₁/l ₂ . Это уравнение задает параболу.

Итак, мы установили, что общее уравнение кривой второго порядка (8) задает одну из следующих кривых второго порядка (sign x означает знак числа x).

sign d	sign s·D	Кривая и ее каноническое уравнение	Кол-во центров
+	–	Эллипс + = 1
+	+	Мнимый эллипс + = –1
–	±	Гипербола – = 1
–		Пара пересекающихся прямых	a2x2 – b2 y2 = 0
+		Пара мнимых пересекающихся прямых	a2x2 + b2 y2 = 0
	±	Парабола y2 = 2pх,
		Пара параллельных прямых x2 = a2 Пара мнимых параллельных прямых x2 = – a2 Пара совпадающих прямых x2 = 0	¥

Примеры решения задач.

1.Составить уравнение кривой, каждая точка которой расположена вдвое дальше от точки F(3, 3), чем от оси Ox. Определить тип кривой и изобразить ее в декартовой системе координат.

Решение. Пусть M(x, y) – произвольная точка кривой, MM¢ – перпендикуляр, опущенный на O. Тогда расстояние от M до Ox равно |MM¢|=|y| (см. чертеж в конце решения), а |MF|= . По условию выполняется

= 2|y| .

Возведение в квадрат, вообще говоря, не является равносильным переходом; но в данном случае обе части равенства неотрицательны. Поэтому, без всяких дополнительных ограничений возводим в квадрат:

(x – 3)² +(y – 3)² = 4y².

Мы раскроем только вторую скобку, и после приведения подобных вновь соберем полный квадрат:

(x – 3)² + y² – 6y + 9 – 4y²= 0,

(x – 3)² –3y² – 6y + 9 = 0,

(x – 3)² –3(y² + 2y + 1 – 4) = 0,

(x – 3)² – 3(y + 1)² = –12.

Делаем замену координат

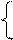x¢= x – 3,

y¢= y + 1.

Она означает перенос начала координат в точку O¢(3,–1). Получившееся уравнение делим на –12:

– = –1.

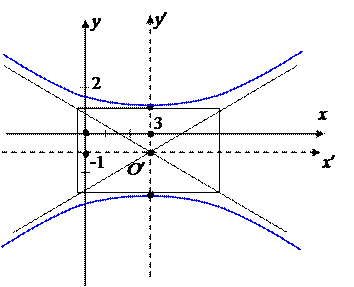
Это уравнение задает гиперболу с полуосями a=2 » 3,4 , b=2. Центр гиперболы находится в точке O¢(3,–1). Подробное описание построения приводится в решении задачи 2а).

2.С помощью переноса начала координат и поворота координатных осей привести уравнение кривой второго порядка к каноническому виду. Определить тип кривой и изобразить её в исходной системе координат:

а)25х² – 14ху + 25у² + 64х – 64у – 224 = 0.

Решение. Общее уравнение кривой второго порядка на плоскости имеет вид:

а₁₁х² + 2а₁₂ху + а₂₂у² + 2а₁х + 2а₂у + с = 0. (8)

Если

d = 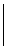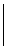¹ 0,

то кривая имеет центр О¢(х_o, у_o), координаты которого можно найти из системы линейных уравнений:

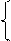a₁₁x_o + a₁₂y_o + a₁ = 0, (10)

a₁₂x_o + a₂₂y_o + a₂ = 0.

Если мы совершим параллельный перенос начала координат в точку О', то уравнение кривой примет вид:

а₁₁х' ² + 2а₁₂ х' у' + а₂₂ у' ² + с' = 0, (9)

где

с' = а₁х_o+ а₂у_o+ с. (12)

Вычисляем:

d = = 576 ¹ 0,

Значит, кривая имеет центр. Найдем координаты центра (х_o, y_o) из системы уравнений (10):

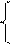
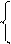25х_o – 7у_o+ 32 = 0, Û 25х_o – 7у_o = –32,

–7х_o+ 25у_o– 32= 0. –7х_o+ 25у_o= 32.

Для решения применим правило Крамера: x_o= , у_o = , где d_x получается заменой первого столбца в d на столбец свободных членов, а d_y – второго столбца:

d_x = = 32· = 32·(–18) = –576.

d_y = 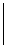= 32· = 32·18 = 576.

x_o= = –1, y_o= = 1.

Значит, центр кривой находится в точке О'(–1, 1). Совершим перенос начала координат в точку О' и получаем новую декартову систему координат О¢х¢у¢. Формулы замены координат имеют вид:

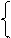x = x' + 1,

у = у' – 1.

Однако делать эту подстановку в исходное уравнение кривой не следует; мы заранее из теории знаем, что получится в результате этой подстановки: уравнение примет вид (9) (то есть линейная часть уравнения исчезнет, а коэффициенты квадратичной части не изменятся), где с' находится по формуле (12):

с' = 32·(–1) – 32·1 – 224 = –288.

Уравнение данной кривой второго порядка в новой системе координат:

25х¢² – 14х¢у¢ + 25у¢² = 288. (9¢)

Далее совершаем поворот координатных осей на угол a, тангенс которого находится по формуле:

а₁₂tg²a + (а₁₁ – а₂₂) ·tga – а₁₂ = 0, (15)

–7tg²a +(25 – 25)tga + 7= 0,

tg²a = 1 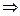tg a₁= 1 или tg a₂ = –1.

Можем выбрать любое из них. Но, как правило, выбираем такое a, для которого tg a > 0. Имеем: a = , sin a = cos a = .

Получим новую систему координат О' х''у''. Формулы замены координат имеют вид:

х¢ = х²соs a – y²sin a,

y¢ = х²sin a + y²cos a .

В нашем случае:

х' = (х'' – y''),

y' = (х'' + y'').

Подставим эту замену в (9¢):

[25(х²– y²)² –14(х²– y²)·(х²+ y²) + 25(х² + y²)² ] = 288

[25х²² – 50х²y²+25 y²² – 14х²+14 y² + 25х²² + 50х²y²+ 25 y²²] = 288.

Слагаемые, содержащие произведение х'' y'' обязательно должны сократиться. Если это не происходит, то следует искать ошибку выше.

[36х'' ² + 64y'' ²] = 288, 9х'' ² + 16y'' ² = 144,

+ = 1.

Это уравнение задает эллипс с полуосями а = 4, b = 3. Строим эллипс.

Для этого сначала строим исходную систему координат Oxy, затем в этой системе находим точку О¢ и строим промежуточную систему координат О¢x¢y¢, которая получается из Oxy переносом начала в точку О'.Затем поворачиваем координатные оси на выбранный нами ранее угол a и получаем окончательную систему координат О¢x²y². Именно на осях этой системы координат мы и откладываем полуоси эллипса.

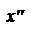
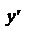
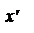
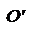
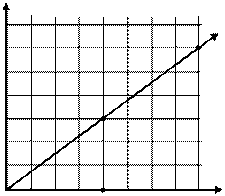В нашем случае a = 45^о, и поэтому повернутые оси легко построить. В более общем случае, если мы нашли, что tg a = a/b , мы этот угол очень легко можем построить на клетчатой бумаге: по оси О'x' мы откладываем отрезок равный b, а по оси О'y' – отрезок равный а. Например, на данном рисунке построен угол, у которого tg a = 3/4 .

б)7x²+16xy-23y²-14x-16y-218=0.

Решение.

d= 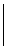=-161-64=-225≠0.

Значит, ищем координаты центра:

7x_o+ 8y_o-7=0, 7x_o+8y_o=7,

8x_o-23y_o-8=0, x_o-23y_o=8.

По правилу Крамера:

d_x= =-161-64=-225≠0, d_y= =0.

x_o= = -1, y_o= =0.

Значит центр кривой находится в точке O'(1, 0). Совершаем перенос начала координат в точку О' и получаем новую декартову систему координат O' х' у'. Формулы замены координат:

x = x¢ +1,

y = y¢

Находим c¢ = -7x_o-8y_o+c = -7-218 = -225. Значит в новой системе координат уравнение кривой примет вид:

7x¢ ² + 16x¢y¢ - 23y¢ ² -225 = 0. (*)

Совершаем поворот координатных осей на угол a , тангенс которого находим из уравнения (5):

8tg²a +30tga -8=0,

4tg²a +15tga -4=0,

D =225+64=289,

tga₁= = , tga₂= = -4.

Выбираем положительный тангенс: tga = . Находим sina = , cosa = . В уравнении (*) делаем замену:

[7(4x"-y")²+16(4x"-y")(x"+4y")-23(x"+4y")²]=225,

[112 x"²-56 x"y"+7y"²+64 x"²+240 x"y"-64y"²–

-23x"²-184x"y"-368y"²]=225

При приведении подобных, слагаемые содержащие произведения x"y" должны сократиться. Если этого не происходит, следует искать ошибку выше.

[153 x"²-425y"²]=225,

9x"²-25y"²=225,

- =1.

Получилось уравнение гиперболы с полуосями a = 5, b = 3.

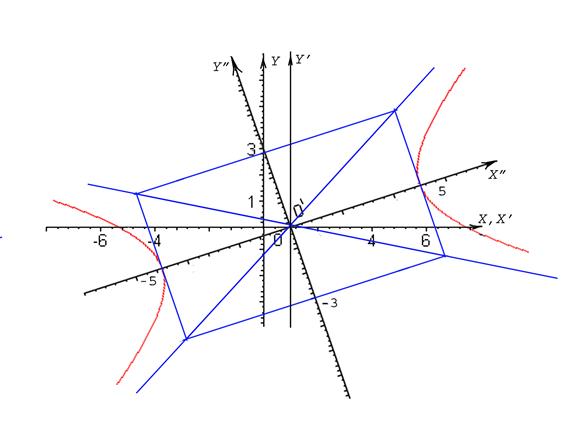
Описание построения:

1) О¢(1, 0) - новое начало координат, О¢x¢||Оx, О¢y¢||Оy - вспомогательные оси;

2) совершаем поворот координатных осей, зная что tg α = 1/4 ; получаем новые координатные оси О¢х" и О¢y" (способ построения см. в конце решения задачи 2а)).

3) в новой системе координат О¢х"y" строим фундаментальный прямоугольник: a = 5, b = 3 ;

4) проводим диагонали фундаментального прямоугольника, они будут являться асимптотами гиперболы;

5) строим гиперболу: она стремится к асимптотам, касаясь фундаментального прямоугольника.

в)9x² - 24xy + 16y² - 20x + 110 y - 50 = 0.

d = = 0

В данном случае не можем применить процедуру нахождения центра и сразу поворачиваем координатные оси:

-12 tg²a-7tga+12 =0,

D=49+576=625,

tg a₁ = = , tg a₂ = = – .

sina= ; cosa= .

Поскольку это первая замена координат, то вид формул отличается от (6) количеством штрихов. Подставляем в первоначальное уравнение:

[9(4x¢ - 3y¢)² - 24(4x¢ - 3y¢)(3x¢ + 4y¢) + 16(3x¢ + 4y¢)²] –

- (4x¢ - 3y¢) + (3x¢ + 4y¢) - 50 = 0,

[144 x¢ ² -216 x¢y' +81y¢ ²-288 x¢² -168 x¢y¢ +288 y¢ ²+ 144 x¢² +384x¢y¢ +296y¢ ²] -

– 16 x¢ + 12 y¢ + 66 x¢ + 88 y¢-50 = 0 .

Слагаемые с x¢y¢ должны сократиться. Кроме того, если d = 0, то одна из переменных в квадрате сокращается полностью:

25 y¢ ² + 50 x¢ + 100y¢ -50 = 0, Û y¢ ² + 2x¢ + 4y¢ - 2 = 0 . (*)

Выделяем полный квадрат:

(y¢² + 4y¢ + 4) - 4 + 2x¢ - 2 = 0,

(y' + 2)² + 2(x' – 3) = 0.

Делаем замену координат:

Она равносильна переносу начала координат в точку O¢(3,-2)_О¢x¢y¢. Подчеркнем, что это координаты относительно второй системы координат О¢x¢y¢.

y"²=–2x" –парабола.

Ее параметр p = 1, а ось параболы – О¢x".

Описание построения:

1. совершаем поворот координатных осей, зная что tg α = 3/4 ;

2. новое начало координат О¢(3,–2) в системе координат Оx¢y¢ ;

3. координатные оси О¢x" и О¢y".

4. для построения параболы любым способом находим дополнительную точку; например, подставим в уравнение (*) y¢= 0, тогда x¢ = 1. Т.е. А(1, 0)_О¢x¢y¢ - дополнительная точка (в системе Оx¢y¢).