Роль вектора и матрицы корреляции множественной линейной модели при подборе объясняющих переменных

Объясняющие переменные в линейной эконометрической модели должны обладать следующими свойствами:

• иметь высокую вариабельность;

• быть сильно коррелированными с объясняемой переменной;

• быть слабо коррелированными между собой;

• быть сильно коррелированными с представляемыми ими другими переменными, не используемыми в качестве объясняющих*.

Объясняющие переменные подбираются с помощью статистических методов.

Процедура подбора переменных состоит из следующих этапов:

1.На основе накопленных знаний составляется множество так называемых потенциальных объясняющих переменных (первичных переменных), в которое включаются все важнейшие величины, влияющие на объясняемую переменную. Такие переменные будем обозначать Х1 Х2,.., Хт.

2.Собирается статистическая информация о реализациях как объясняемой переменной, так и потенциальных объясняющих переменных. Формируется вектор у наблюдаемых значений переменной Y и матрица X наблюдаемых значений переменных Х1, Х2, ..., Хт в виде

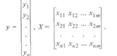
3. Исключаются потенциальные объясняющие переменные, характеризующиеся слишком низким уровнем вариабельности.

4.Рассчитываются коэффициенты корреляции между всеми рассматриваемыми переменными.

5.Множество потенциальных объясняющих переменных редуцируется с помощью выбранной статистической процедуры

Вектор и матрица коэффициентов корреляции

Для оценивания силы линейной зависимости объясняемой переменной Y от потенциальных объясняющих переменных Х1, Х2, .., Хт рассчитываются коэффициенты корреляции

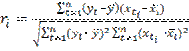
Эти коэффициенты представляются в виде вектора корреляции:

Коэффициенты корреляции между потенциальными объясняющими переменными Х1, Х2, ..., Хт рассчитываются по формуле

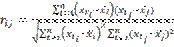
образуют матрицу корреляции R:

Матрица R симметрична, т. е. rij= rji

Свойства дисперсии случайной переменной

Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата её отклонения от математического ожидания: D(X)=M[X-M(X)]² или D(X)=M(X-a)² где a=M(X).

(Для дисперсии СВ Х используется также обозначение Var(X).)

Дисперсия характеризует отклонение (разброс, рассеяние, вариацию) значений СВ относительно среднего значения.

Если СВ Х – дискретная с конечным числом значений, то

.

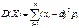Дисперсия D(X) имеет размерность квадрата СВ, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину .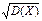

Свойства дисперсии СВ:

1) D(C)=0, где C – постоянная величина;

2) D(kX)=k²D(X);

3) D(X)=M(X²)-a² где a=M(X);

4)D(X+Y)=D(X-Y)=D(X)+D(Y), где X и Y – независимые случайные величины.