Формула полной вероятности

Пусть в результате испытания может произойти одно из n событий Н₁, Н₂, …, Н_n, которые удовлетворяют следующим условиям:

1. они являются попарно несовместными Н_iH_j=Æ;
2. хотя бы одно из них в результате испытаний обязательно произойдёт, т.е. их объединение есть достоверное событие

H₁È H₂È ….È H_n=Ω

События Н₁,…Н_n, удовлетворяющие условиям 1 и 2, называются гипотезами.

На первой лекции было дано определение полной группы попарно несовместных событий и обещано, что мы с ними будем детально разбираться. Гипотезы образуют именно такую группу.

Пусть также имеется некоторое событие А и известны вероятности гипотез Р(Н1),…, Р(Hn), которые предполагаются ненулевыми, и условные вероятности события А при выполнении этих гипотез P(A|H₁), P(A|H₂), …, P(A|H_n). Как найти вероятность события А?

V Дано два набора деталей. Вероятность того, что деталь стандартная в 1-ом ящике - Р₁ , во втором - Р₂ .Наугад был выбран ящик и из него была взята деталь. Найти вероятность того, что деталь стандартная.

Ï Выдвинем гипотезы:

Н1 – взяли деталь из первого ящика, Н2 – взяли из второго ящика. Н1 и Н2 образуют полную группу событий. Поскольку ящик выбран наугад, то Р(Н1)=Р(H2)=0.5. Вероятность того, что деталь стандартная, при условии, что ее взяли из первого ящика P(A|H₁)= Р_1. Вероятность того, что деталь стандартная, при условии, что ее взяли из второго ящика P(A|H₂)= Р₂. Требуется найти Р(А)

Теорема. Пусть для некоторого события А и гипотез Н₁,…, Н_n известны вероятности гипотез P(H₁),…., P(H_n) и условные вероятности P(A|H₁), P(A|H₂), …, P(A|H_n). Тогда безусловная вероятность Р(А) определяется по формуле:

Р(А) = P(H₁) Р(A|H₁)+…+ P(H_n) P(A|H_n),

Которая называется формулой полной вероятности.

Доказательство.

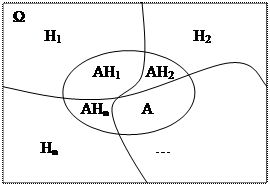Представим событие

А=А*Ω=А*(Н₁+Н₂+…+H_n) = AH₁ + AH₂ + … AH_n – несовместны.

Р(А)= Р(AH₁)+ Р(AH₂)+…+ Р(AH_n)=*

По формуле умножения вероятности

Р(AH₁) = P(H₁) Р(A|H₁)

Р(AH₂) = P(H₂) Р(A|H₂)

………………………..

Р(AH_n) = P(H_n) Р(A|H_n)

*= P(H₁) Р(A|H₁) + … + P(H_n) Р(A|H_n). <

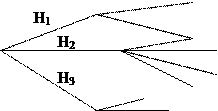V Путник должен попасть из В в А в соответствие со схемой дорог. Выбор пути равновозможен. Найти вероятность Р(А) - достижения пункта А.

(Сеть дорог – сеть каналов передачи информации.

Р(А) – вероятность передачи информации А

по такой сети). В

Гипотезы

H₁ , H₂ , H₃ – выбор пути. P(H₁)= P(H₂)= P(H₃)=1/3

Р(A|H₁)= ½, Р(A|H₂)= ¼, Р(A|H₃)= 0

Р(А)= P(H₁) Р(A|H₁)+ P(H₂) Р(A|H₂)+ P(H₃)Р(A|H₃)=1/3*½+1/3*¼=¼. N

ФОРМУЛЫ БАЙЕСА

Пусть по прежнему событие А может произойти с одним из событий Н₁,…, Н_n, являющимися гипотезами. Предположим, что известны вероятности гипотез Р(Н_i) и в результате испытания событие А произошло, т.е. получена дополнительная информация. Поставим своей задачей определить, как изменилиь вероятности гипотез (ведь мы теперь обладаем дополнительной информацией), т.е. чему будут равны P(H₁| A) – вероятность i-й гипотезы, при условии что событие А произошло.

Теорема. Пусть для некоторого события А, Р(А) > 0 и гипотез Н₁,…, Н_n известны вероятности гипотез P(H₁),…., P(H_n) и условные вероятности Р(A|H₁), P(A|H₂), …, P(A|H_n). Тогда условная вероятность P(H_i| A) гипотезы Hi при условии события А определяется формулой Байеса

.

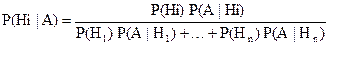Доказательство.

По формуле умножения вероятностей Р(AH_i)= Р(А) P(H_i|A). Отсюда P(H_i|A) = Р(AH_i)/ Р(А) (*), где Р(А) – формула полной вероятности события А.

С другой стороны, по этой же формуле Р(AH_i)= P(H_i) Р(A|H_i). Подставляя это выражение в (*)получим

.<

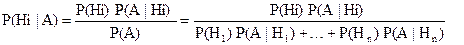Вероятности P(H_i) называются априорными (J до того), а P(H_i|A) – апостериорными (J после того).

Формула Байеса находит широкое применение в математической статистике, теории принятия решений. Смысл байесовского подхода заключается в том, что мы выдвигаем некоторые априорные вероятности (достаточно произвольные), а потом, учитывая результаты повторяющегося эксперимента, мы определяем апостериорные вероятности гипотез.

Байес (Бейес) Томас

1702-1761