Полная система уравнений Максвелла
Полная система уравнений Максвелла представляет собой систему дифференциальных или интегральных уравнений, решение которых позволяет определить характеристики электрического и магнитного поля в любой точке пространства в любой момент времени. Эти уравнения удовлетворяют динамическому принципу причинности или лапласовскому детерминизму.
Согласно этим уравнениям, если известно распределение зарядов в пространстве и заданы характеристики электрического и магнитного поля в начальный момент времени, а также заданы характеристики среды, то можно найти характеристики электрического и магнитного поля в любой момент времени в любой точке пространства.
Полная система уравнений Максвелла имеет вид, представленный в таблице:
| Номер уравнения | Закон | Уравнение Максвелла в дифференциальной форме | Уравнение Максвелла в интегральной форме |
| Закон Био – Савара - Лапласа | 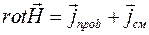 | 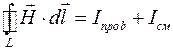 | |
| Закон Фарадея для электромагнитной индукции | 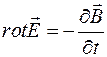 | 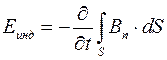 | |
| Вихревой характер магнитного поля | 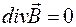 | 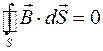 | |
| Теорема Остроградского - Гаусса | 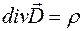 | 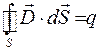 | |
| Определение вектора электрической индукции | 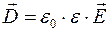 | - | |
| Определение вектора индукции магнитного поля | 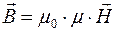 | - | |
| Закон сохранения электрического заряда | 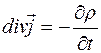 | 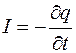 | |
| Закон Ома для полной цепи | 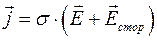 | 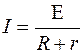 |
