Расчет изгиба статически неопределимых балок

8.10.1. Однопролетные балки

Статически неопределимыми будут балки, у которых все реакции не могут быть определены из одних лишь уравнений статики. Так, балка на рис. 8.44,а имеет три неизвестные реакции 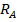, , 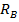и и 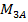всего два уравнения статик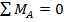и и 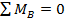. А для балки на рис. 8.44, б неизвестных реакций четыре: 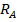, , 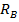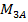и 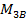. Число же уравнений статики, как и в предыдущем случае, те же два условия равенства нулю всех моментов относительно опорных закреплений.

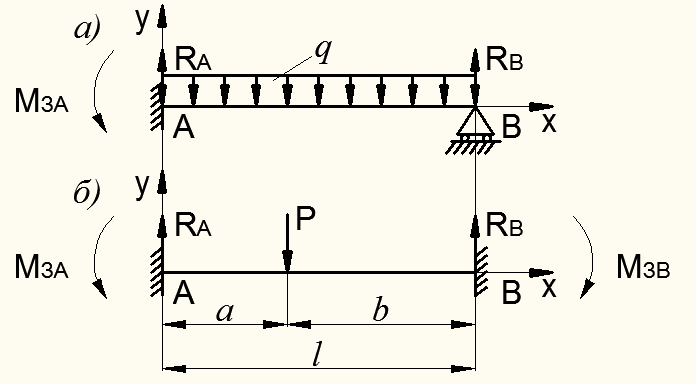
Рисунок 8.44 – Статически неопределимые однопролетные _балки

Разность числа реакций 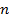и числа уравнений статики 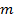называется степенью статической неопределимости балки .

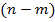Для балки на рис.8.44,а степень статической неопределимости будет 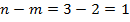: говорят, что балки единожды статически неопределённа. Для балки на рис.8.44,б 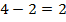, т.е. балка дважды статически неопределенна. Таким образом, у статически неопределенных балок имеются так называемые «лишние» неизвестные по отношению к числу уравнений статики. Для их определения используются условия совместности деформаций, составление которых рассмотрим на следующих примерах:

Пример 9.9.1. Раскрытие статической неопределимости и расчет изгиба балки (рис.8.45, а).

Решение

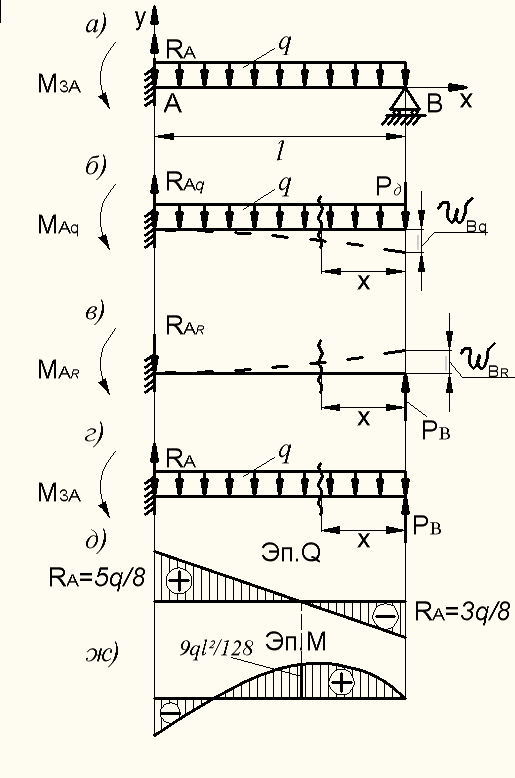Если за лишнюю неизвестную принять реакцию 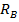, то при мысленном отбрасывании опоры В должно выполняться такое условие совместности деформаций (рис. 8.45, б, в):

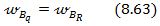
где – прогиб балки от нагрузки q при мысленном удалении опоры В (см. рис. 8.45, б); – прогиб балки от силы (реакции) 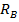(см. рис. 8.45, в).

Вычислим эти прогибы на основании интеграла Мора.

m NOkyOp9i7McQfnDFESSvBgoeBGqkw6lXsvFF+M+HYaln7aUuguyYVIOMGSt9oNEzN3Do+rwPfZtO /GPPcQ7FDok1MEw5biUKNZgvlHQ44Rm1nzfMCErUa43NmY8nE78SQZlMzxJUzKklP7UwzREqo46S QVy5sEY+bw2X2MRSBn7vMznkjJMbaD9smV+NUz143f8Lln8AAAD//wMAUEsDBBQABgAIAAAAIQCB 51Rj4AAAAAsBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI/BToNAEIbvJr7DZky80QWCrUWWxmjszRjR VI8LOwKRnSXstsU+fceTHmfmyz/fX2xmO4gDTr53pCBZxCCQGmd6ahW8vz1FtyB80GT04AgV/KCH TXl5UejcuCO94qEKreAQ8rlW0IUw5lL6pkOr/cKNSHz7cpPVgceplWbSRw63g0zjeCmt7ok/dHrE hw6b72pvFfgmXu5esmr3UcstntbGPH5un5W6vprv70AEnMMfDL/6rA4lO9VuT8aLQUGUJTfsHhRk 6QoEE1Gy5kXN6CpOQZaF/N+hPAMAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAA AAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAA AJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQDOG/K/RAIA AFMEAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQCB51Rj 4AAAAAsBAAAPAAAAAAAAAAAAAAAAAJ4EAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAA qwUAAAAA " strokecolor="white [3212]">

Рисунок 9.45 – К расчету статически неопределимой балки

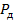При определении прогиба в т. В от распределенной нагрузки q мысленно введем дополнительную силу (см. рис. 8.45, б):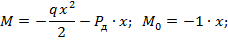

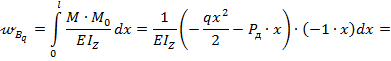
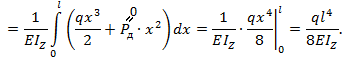
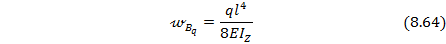
Прогиб конца консоли от силы 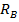равен (см. рис. 8.45, в):

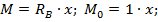
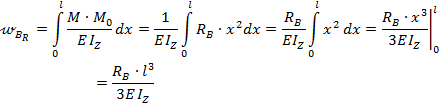
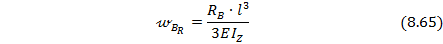
На основании условия (8.63) приравниваем выражения (8.64) и (8.65)для прогибов балки в т. В:

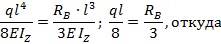
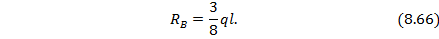
Найдя 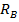, получаем статически определимую балку, нагруженную поперечной распределенной нагрузкой интенсивностью q и уже определенной силой (реакцией) 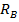(рис. 8.45, г). Для этой балки строим эпюры и M (рис. 8.45, д, ж). отсчитывая координату х от правого конца балки т. В.

Для эп. имеем:

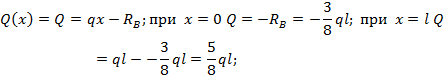
откладываем полученные ординаты на эп. и соединяем их прямой линией – линейная зависимость эп. (см. рис. 8.45,д).

Для эп. М имеем:

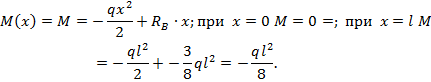
Как видно из выражения для 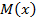, эпюра изгибающего момента соответствует квадратической параболе относительно координаты х. Две ее ординаты в т.т. А, В уже определены. Для нахождения ординаты эп. М в сечении, где 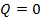, проводим дополнительные вычисления.

Из условия экстремума функции М получаем:

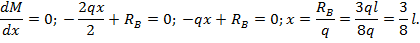
В сечении балки при 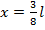имеем экстремум функции М в пролете балки:

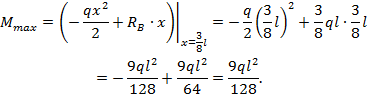
Полученную ординату 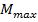откладываем на эп. М при 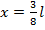(см. рис. 8.45, ж).

Пример 9.9.2.Для балки, которая защемлена обеими концами (рис. 8.46, а) и изгибается сосредоточенной силой Р, раскрыть статическую неопределенность и построить эпюры и .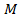

Решение

Как было указанно выше, рассматриваемая балка дважды статически неопределима: неизвестных реакций – четыре 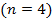, а условий статики – два .

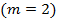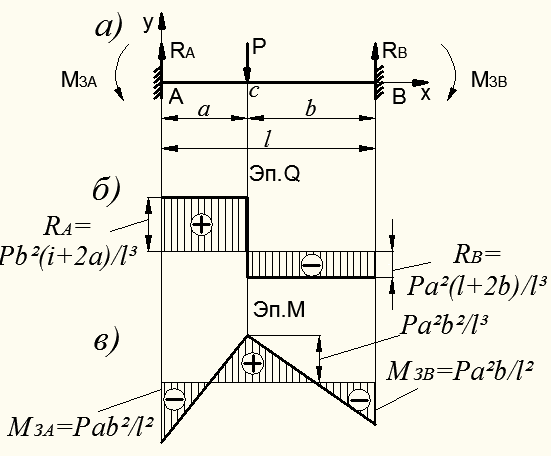
Рисунок 8.46 – К расчету статически неопределимой балки

Из условий статики имеем:

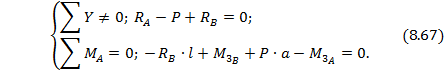
Учитывая, что угол поворота и прогиб опорного сечения В равны нулю, получаем два недостающих уравнения для определения реакций – условия совместности деформаций:

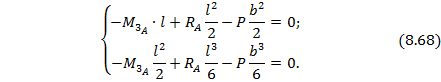
Решая полученные системы уравнений (8.67) и (8.68) находим реакции:

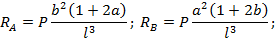
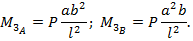
Теперь легко построить эпюры перерезывающих сил и изгибающих моментов 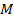. Для этого вычисляем изгибающий момент в сечении С под силой Р:

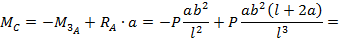
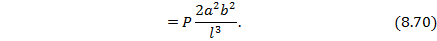
Эпюры и 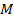показаны на рис. 8.46, б, в.

8.10.2. Неразрезные многопролетные балки

Неразрезными многопролетными называются балки, имеющие более одного пролета. Они являются статически неопределимыми и раскрытие их статической неопределимости удобно выполнять методом уравнений трех моментов. На простейшем примере рассмотрим суть этого метода.

Пример 9.3.Для балки (рис. 8.47, а) кроме шарнирных опор по концам имеется промежуточная опора. Неизвестными в расчете изгиба такой балки являются три реакции на опорах, а условий статики – два. Поэтому такая балка будет единожды статически неопределимой.

В раскрытии статической неопределимости по теореме трех моментов за лишние неизвестные принимаются опорные моменты М на промежуточной опоре 2. При мысленном разрезании ее и разделении балки на две однопролетные (рис.8.47, б), эти моменты определяются из условия совместности деформаций:

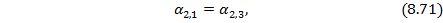
где 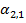– угол поворота правого опорного сечения 2 однопролетной балки между опорами 2 и 1;

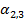– угол поворота левого опорного сечения 2 однопролетной балки между опорами 2 и 3.

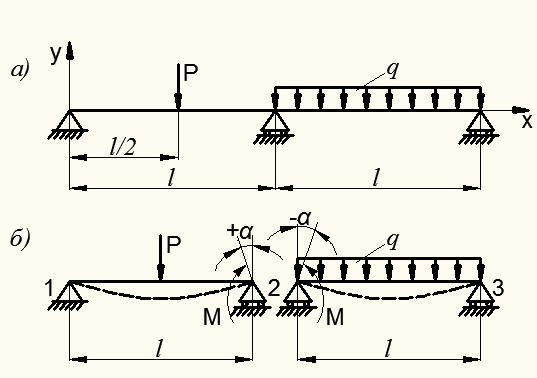
Рисунок 8.47 – К расчету двухпролетной балки по теореме трех _моментов

Эти углы поворота с учетом правила знаков (см. рис. 8.47, б) выражаются через внешнюю нагрузку и опорные моменты:

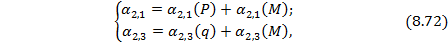
где

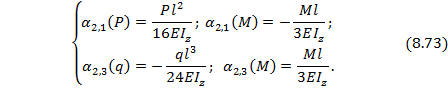
На основании выражений (8.72) и (8.73) с учетом (8.71) получаем уравнение по определению лишней неизвестной М:

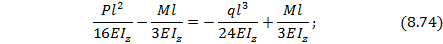
откуда

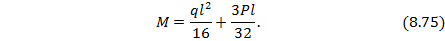
После нахождения лишней неизвестной 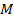каждый пролет балки рассматривается как статически определимые балки, загруженные кроме внешней нагрузки уже определенными опорными моментами .

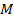Метод раскрытия статической неопределимости многопролетных балок по теореме трех моментов называется так потому, что при произвольном числе пролетов балки 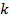в каждое уравнение совместности угловых деформаций типа (8.74) будет входить не более трех опорных моментов для рассматриваемой -й промежуточной опоры при условии типа (8.71).

Расчет элементов изгиба каждого из пролетов после определения лишних неизвестных, как статически определимой балки, производится методом наложения (суммирования) элементов изгиба от внешней пролетной нагрузки и уже определенных опорных моментов. Так, в рассматриваемом примере результирующая эпюра изгибающих моментов для каждого пролета балки 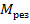, получается путем наложения эп. 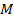от заданной пролетной нагрузки 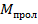на эп. 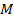от опорных моментов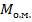

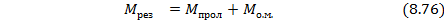
Для рассмотренного примера она показана заштрихованной на рис. 8.48:

Для первого пролета 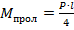, для второго пролета 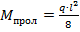. Таким наложением определяются реакции на опорах и строится эп. .

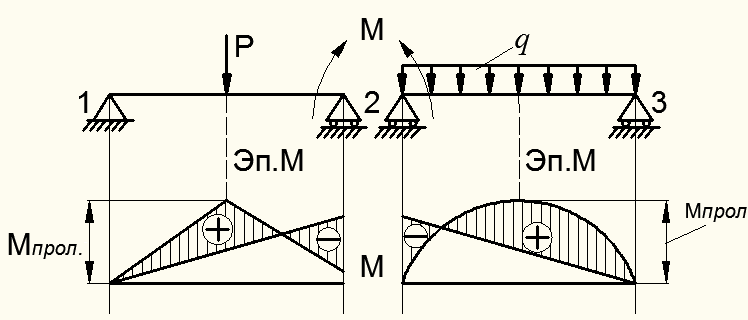
Рисунок 8.48 – Построение эпюры изгибающих моментов методом наложения