Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формула Байеса. Теорема Бернулли
1. Вероятность появления однородных членов в произведениях И.А. Гончарова равна 0,22, а в произведениях А.Н. Толстого – 0,12. Из сборников произведений И.А. Гончарова и А.Н. Толстого выбирается произвольно по предложению. Найти вероятность того, что… а) оба выбранных предложения будут содержать однородные члены; б) ни одно не будет содержать однородные члены; в) хотя бы одно из предложений будет содержать однородные члены.
2. Студент нашёл нужную информацию в одной из 7 книг, но забыл, в какой из них. Определить вероятность, что для повторного использования той же информации, ему придётся пересмотреть три книги.
3. В авторской художественной речи прозы К. Федина вероятность появления имён существительных равна 0,392, а прилагательных – 0,134. Выбираются два слова из произведения К. Федина. Какова вероятность событий: а) «оба слова относятся к одной части речи»; б) «выбранные слова относятся к разным частям речи».
4. Статистическая вероятность появления глагольных форм в молдавском публицистическом тексте равна 0,156. Найти вероятность того, что среди 5 наугад выбранных словоупотреблений из молдавского текста, глагольная форма встретится а) 2 раза; б) более 3 раз.
5. С целью обеспечения надежности корреспондент передает сообщение в редакцию двумя способами, каждый из которых может привести как к успеху, так и закончиться неудачно. Вероятность успешной передачи сообщения первым способом равна 0.9, при использовании второго – 0.80. В результате проведенных мероприятий редакция получила сообщение. Определить вероятность того, что передача редакции сообщения состоялось благодаря первому способу.
Задание 4 Случайные величины
| Х | -1 | |||
| Р | 0,1 | 0,2 | 0,3 | 0,25 |
1) Найдите математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение σ(Х) случайной величины Х, если закон её распределения задан таблицей.
2) Вероятность появления буквы К в русских литературных текстах равна 0,128. Произвольно выбирают 3 буквы. Необходимо:
а) составить закон распределения случайной величины X – «число появлений буквы К»;
б) найти математическое ожидание М(Х) и дисперсию D(Х) этой случайной величины;
в) найти функцию распределения F(x) и построить её график.
3) Известно, что доля наречий в авторском повествовании и описании в художественной прозе равна 0,07. Найти вероятность того, что в фрагменте текста, длиной 250 словоформ: а) будет 2 наречия; б) менее двух наречий; в) не менее двух наречий.
Найти М(Х) и D(Х) случайной величины X - «число наречий в данном отрывке текста».
4) Случайная величина Х задана дифференциальной функцией распределения
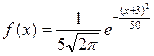
а) По какому закону распределена случайная величина Х?
б) Определите М(Х), D(Х), σ(Х).
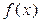в) Постройте график , определив координаты не менее трёх точек графика.
г) Найдите вероятность попадания случайной величины X в интервалы (0; ∞ ) и (-4; 3).
| Y | ||
| Р | 0,7 | 0,3 |
| Х | ||
| Р | 0,1 | 0,9 |
5) Независимые дискретные случайные величины Х и Y заданы своими законами распределения:
Найдите закон распределения СВ Z=X+2Y.
Задание 5 Элементы математической статистики
В ходе исследования средних частот частей речи у русских писателей XIX-XX вв. (было взято 20 однородных фрагментов длиной 500 знаменательных слов из текстов каждого из 14 известных писателей), получены следующие данные о среднем числе наречий:
29;29;43;45;38;45;56;38;45;42;43;44;31;42.
1) Произведите первичную обработку данных:
а) представьте выборку в виде вариационного ряда;
б) определите моду, медиану и размах вариаций выборки;
в) постройте статистический ряд частот и относительных частот;
г) постройте полигон относительных частот;
д) найдите числовые характеристики статистического распределения: среднее выборочное, выборочную дисперсию, исправленную выборочную дисперсию, исправленное среднее квадратическое отклонение;
е)найдите эмпирическую функцию распределения Fn(x) и постройте её график.
2) Предполагая, что частота употребления наречий во всех литературных произведениях распределена по нормальному закону, найдите по выборке 95% доверительный интервал для среднего числа употребления наречий (математического ожидания генеральной совокупности).
3) Сколько фрагментов текста необходимо обработать, чтобы относительная ошибка измерения среднего числа глаголов не превышала 5% с доверительной вероятностью 90%?