Анализ установившегося движения машинного агрегата.

Расчёт маховика.

Технологические машины выполняют технологический процесс в установившемся режиме, который обычно не имеет ограничений по продолжительности. Для машин, содержащих рычажные механизмы, этот режим является неравновесным, при котором кинетическая энергия изменяется периодически, т.е. её значения повторяются через время цикла tц (рис. 16.1). При этом угловая скорость ведущего звена также меняется периодически в зависимости от его положения (рис. 16.2). При этом характер изменения графиков кинетической энергии и угловой скорости обычно не соответствуют друг другу. Периодом изменения, обычно, является один оборот (2p радиан или 360⁰). Такое движение характеризуют средней угловой скоростью w_СР и коэффициентом неравномерности

d = 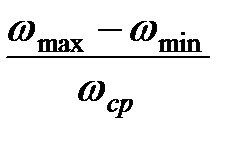. (16.1)

Величина коэффициента неравномерности в технологических машинах мала (d= 0,03…0,05), так как только при этом условии обеспечивается нормальная работа привода. Малость d позволяет использовать при решении уравнения движения приближенные методы.

В данном случае вместо уравнения (15.8) используется

уравнение движения в интегральной форме

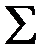Т = Т - Т_н = А . (16.2)

Здесь Т и Т_н –кинетические энергии машинного агрегата в произвольном и начальном положениях. За начальное положение целесообразно брать то, в котором ведомое звено занимает крайнее положение и его скорость равна 0.

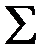А – сумма работ на данном участке всех внешних сил и моментов. Работа сил трения здесь не учитывается.

Рис.16.1

Рис.16.2

Для динамической модели (рис.15.2) после приведения сил и масс уравнение (16.2) приобретает вид

0,5 · J · ω² - 0,5 · ( 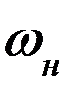)² · J_н = А_д + А_с . (16.3)

Здесь А_Д = 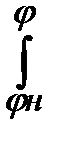М_дdφ -работа движущих сил на участке;

А_С = 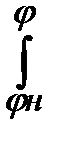М_сdφ -работа сил сопротивления и сил тяжести на участке. Величина А_С при расчётах обычно бывает отрицательной.

Для упрощения записи здесь и далее опускаем значок «пр» при приведённых моментах движущих сил М_Д , сил сопротивления М_С и приведённых моментах инерции .

Анализ уравнения (16.3) показывает, что причинами колебаний угловой скорости ведущего звена механизма являются:

а) несоответствие величин приведённого момента М_Д движущих сил и приведённого момента М_С сил сопротивления. Это приводит к появлению избыточной работы

А_и = А_д + А_с . (16.4)

б) непостоянство приведённого момента инерции динамической модели при наличии в механизме масс, совершающих возвратно-поступательное, качательное и сложно-плоское движения.

Величина и характер изменения сил сопротивления задаются при проектировании. Следовательно, путём интегрирования можно в каждом положении механизма определить величину работы А_с. Обозначим работу А_с за период (один оборот кривошипа ) .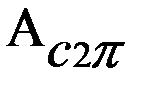

При установившемся неравновесном движении движущие силы или моменты за период совершают одинаковую работу, т. е. = - .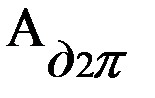

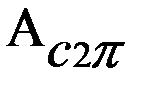Момент движущих сил М_Д зависит от угловой скорости ω, однако при малых изменениях скорости можно приближённо принять М_Д = соnst.

Тогда А_Д = М_Д · φ, где 0 ≤ φ ≤ 2π.

Величина движущего момента М_Д = ( 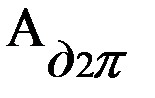) / 2π. (16.5)

Изменение кинетической энергии агрегата, равное избыточной работе, определится по зависимости:

Т = А_И = М_Д · φ + 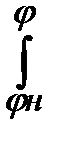М_С dφ. (16.6)

Подставляя в уравнение движения (16.3) зависимости (15.7) и (16.2), после преобразований можно получить

Т = Т_С + Т_V . (16.7)

Здесь Тc = 0,5J_c (ω² - 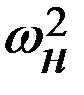) (16.8)

Тc - изменение кинетической энергии вращающихся масс;

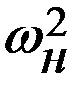Т_V= 0,5·J_V·ω² - 0,5·J_Vн· - изменение кинетической энергии масс, совершающих сложно-плоское и возвратно-поступательное движения.

Из-за малости коэффициента неравномерности хода (δ = 0,03…0,05) справедливо приближённое равенство ω ≈ ω _н ≈ ω _ср .

Поэтому можно принять:

Т_v ≈ 0,5 • 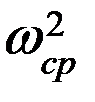(J_v - J_vн). (16.9)

Отсюда находится в каждом положении механизма приращение кинетической энергии вращающихся масс:

Т_C = Т - Т_V . (16.10)

Величина Т_C, периодически меняясь, достигает в каких-то положениях максимальных 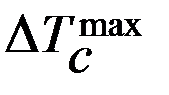и минимальных 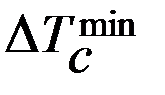значений. Соответственно, в этих положениях угловая скорость будет достигать также значений ω_max и ω_min. Используя зависимости (16.10), (16.9), (16.6), (16.1), считая приближённо

ω_ср = 0,5(ω_max + ω_min ), можно получить, что наибольший перепад кинетической энергии вращающихся масс

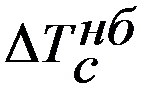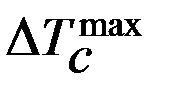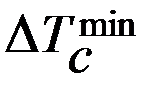= - = J_С ∙ δ ∙ 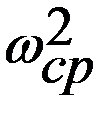. (16.11)

Если при проектировании задана величина коэффициента неравномерности δ, то из зависимости (16.11) находится необходимая для этого величина J_c приведённого момента инерции вращающихся масс:

J_c = 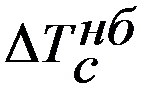/ (δ ∙ 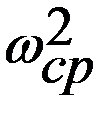). (16.12)

Величина J_c, получаемая из зависимости (16.12), обычно не может быть обеспечена за счёт приведённого момента инерции J_co имеющихся вращающихся масс агрегата. В этом случае на ведущем валу исполнительного механизма устанавливается маховик с моментом инерции:

J_М = J_c – J_co . (16.13)

Маховик (рис.16.3 ) представляет собой отбалансированное колесо, масса которого сосредоточена, в основном, на ободе. Он является аккумулятором кинетической энергии. Когда работа двигателя оказывается в избытке, маховик накапливает кинетическую энергию, которая потом используется при выполнении технологического процесса. Чем больше J_c (а следовательно, и J_М), тем выше аккумулирующая способность маховика, тем меньше будут колебания ω при колебаниях потока кинетической энергии, тем равномернее будет вращаться ведущее звена механизма.

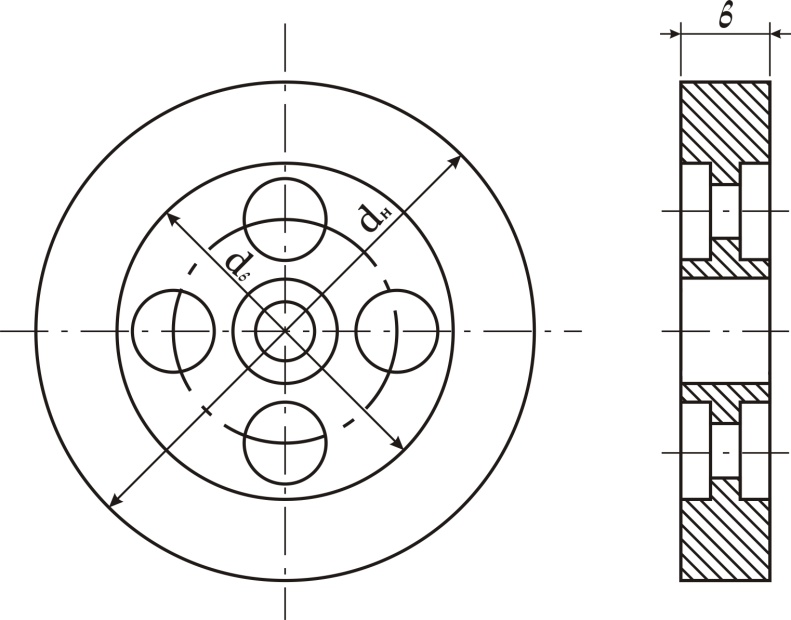Рис.16.3

Отклонение угловой скорости от её среднего значения ω_ср можно найти, так как известно приращение 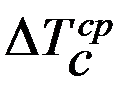кинетической энергии в положении, где ω=ω_ср .

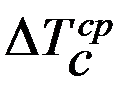= 0,5( 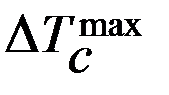+ 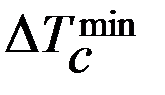). (16.14)

В каждом положении Т_С - = - .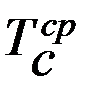

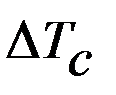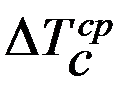Раскрывая это уравнение, получаем

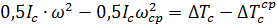(16.15)

Представим ω = ω_ср + Δω. (16.16)

Из уравнения (16.15), используя зависимость (16.16) и принимая приближённо Δω² = 0, после преобразований получим:

Δω = ( Т_С - 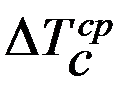) / (ω_ср ∙ J_C) . (16.17)

Следует отметить, что в данных методических указаниях рассматривается решение уравнения движения для случая, когда не учитывается влияние колебаний угловой скорости на величину движущего момента двигателя.

Однако, имеются машины, в которых влияние скорости на силы и моменты достаточно сильно. К ним относятся, например, асинхронные и шунтовые двигатели, получившие большое распространение в промышленном электроприводе.

В этом случае приведённое выше решение может быть принято, как первое приближение. Уточнённое решение, которое можно получить методом последовательного приближения, приводится в работах [1], [4] . Оно всегда даёт решение с несколько меньшей величиной J_C . Это позволяет использовать маховики с меньшим моментом инерции, а следовательно, с меньшими габаритами и металлоёмкостью.

Лекция №17.