Качественная оценка коэффициента корреляции

Если r_ху имеет максимальное значение, равное единице, то мы имеем дело со строгой линейной положительной зависимости между выборочными значениями x и у (на диаграмме рассеяния все точки находятся точно на восходящей прямой линии).

Если r_ху принимает минимальное значение -1, когда существует линейная отрицательная зависимость (точки лежат точно на нисходящей прямой линии). Последняя ситуация часто наблюдается при рассмотрении зависимости спроса на товар от его цены.

Величина r_ху = 0 показывает, что зависимость между наблюдениями x и у в выборке отсутствует.

Теснота связи	Величина линейного коэффициента корреляции
Прямая связь	Обратная связь
Практически отсутствует	0,1 – 0,3	(-0,1) – (-0,3)
Слабая	0,3 – 0,5	(-0,3) –(- 0,5)
Умеренная	0,5 – 0,7	(-0,5) – (-0,7)
Сильная	0,7 – 1,0	(-0,7) – (-1,0)

Оценка значимости коэффициента парной корреляции

Любая совокупность наблюдений представляет собой некоторую выборку. Значит, значение любого показателя, рассчитанное на основе этой выборке, не может рассматриваться как истинное. В связи с этим, возникает необходимость проверки значимости этого показателя.

Для оценки значимости коэффициента корреляции применяется t - критерий Стьюдента. Фактическое значение этого критерия рассчитывается по формуле:

.

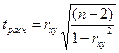Вычисленное по этой формуле значение 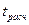сравнивается с табличным значением t-критерия, которое берется из таблицы значений t-Стьюдента с учетом заданного уровня значимости и числа степеней свободы (α = 0,05 или 0,01, k = n -2 ).

Если 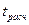> 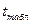, то полученное значение коэффициента корреляции признается значимым. Таким образом, делается вывод о том, что между исследуемыми переменными есть статистическая взаимосвязь.

Парный коэффициент детерминации

Зная линейный коэффициент корреляции, можно рассчитать парный коэффициент детерминации r²_ху. Он показывает, какая доля вариации переменной Y учтена в модели и обусловлена влиянием на неё переменной X.

Пример

По представленным данным о спросе и доходе населения за ряд текущих лет определить степень влияния дохода населения на его спрос. Оценить значимость коэффициента корреляции.

Год	Доход, Х	Спрос, Y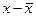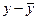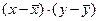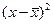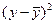
			-5	-3,3	16,5		10,89
			-3	-1,3	3,9		1,69
			-1	-1,3	1,3		1,69
		10,3
		10,5		1,2	3,6		1,44
				3,7	18,5		13,69
Итого		55,8			44,80	70,00	30,40
Среднее		9,3			7,47	11,67	5,07

Средние значения случайных величин Х и Y рассчитаем по формулам, соответственно:

.

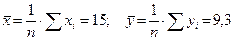Стандартные ошибки случайных величин Х и Y рассчитаем по формулам, соответственно:

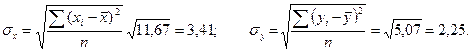
Рассчитаем ковариацию:

.

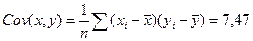Аналогичные расчеты можно получить, используя встроенные возможности электронных таблиц Excel: КОВАР(массив1; массив2), которая возвращает ковариацию, то есть среднее произведений отклонений для каждой пары точек данных.

Синтаксис функции:

Массив1 — это первый массив или интервал данных.

Массив2 — это второй массив или интервал данных.

Рассчитаем коэффициент парной корреляции:

.

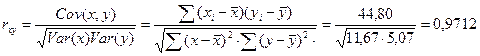Аналогичные расчеты также можно получить, используя встроенные возможности электронных таблиц Excel: КОРРЕЛ(массив1;массив2), которая возвращает коэффициент корреляции меду интервалами ячеек массив1 и массив2.

Синтаксис функции:

Массив1 — это ячейка интервала значений.

Массив2 — это второй интервал ячеек со значениями.

Оценим значимость коэффициента корреляции.

Для этого рассчитаем значение t – статистики:

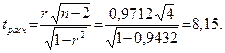
Табличное значение критерия Стьюдента равно:

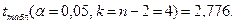
Воспользуемся встроенными возможности электронных таблиц Excel: функция СТЬЮДРАСПОБР(вероятность;степени_свободы) возвращает t-значение распределения Стьюдента как функцию вероятности и числа степеней свободы.

Синтаксис функции:

Вероятность - вероятность, соответствующая двустороннему распределению Стьюдента (α = 0,05 или 0,01).

Степени_свободы— число степеней свободы, характеризующее распределение (k = n -2).

Сравним числовые значения критериев:

.

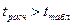Полученное значение коэффициента корреляции значимо.

Вычислим парный коэффициент детерминации:

r²_ху = 0,9432.

Таким образом, доход населения (Х) оказывает весьма высокое влияние на спрос (Y). На 94% спрос населения зависит от дохода. Оставшиеся 6% (100 – 94) - это влияние неучтённых факторов.

Регрессионный анализ

После установления наличия корреляционной зависимости между признаками, экономистов интересует установление аналитической формы этой зависимости. Это является основной задачей регрессионного анализа.