Дискретное преобразование Фурье

Спектральная плотность 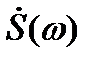дискретизированного сигнала 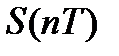определяется выражением

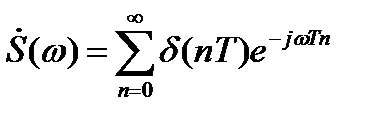
(4.1)

Согласно (4.1) спектр континуального дискретизированного сигнала сплошной. Но он является таковым лишь при условии, что объем выборки временных отсчетов сигнала бесконечен.

В практических приложениях мы всегда имеем дело с конечной выборкой отсчетов сигнала. Более того по многим причинам желательно вычислить ПФ на ЭВМ, это значит, что необходимо рассматривать конечное число дискретных отсчетов.

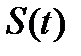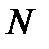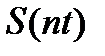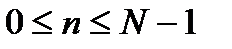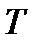Предположим, что временная функция представлена последовательностью из отсчетов , , где период дискретизации во временной области. С вычислительной точки зрения удобно допустить также, что спектр 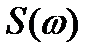представлен последовательностью из 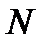отсчетов 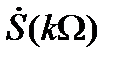,где период дискретизации в частной области.

Будет исходить из предположения, что 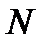- выборочной временной последовательности сигнала ставятся в соответствии 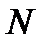- выборочная последовательность из частотной области.

Заменив в (4.1) непрерывную величину 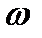дискретной 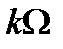и положив пределом переменной 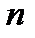значение 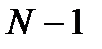, получим

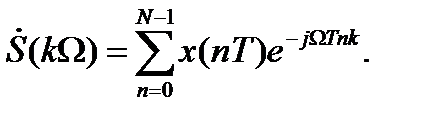(4.2)

Выражение (4.2)полностью дискретно, как во времени, так и по частоте и поэтому подходит для вычислений на ЭВМ.

Если в (4.2) положить , то получим

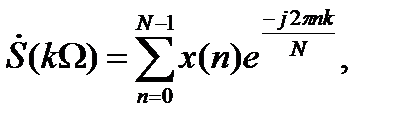(4.3)

при таком определении получим 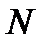значений гармоник спектра.