Двумерное преобразование Фурье
Операции многоканальной обработки могут быть определены как операции, которые должны работать одновременно на нескольких трассах. Многоканальные процессы могут быть полезными для различения сигнала на фоне помех и улучшения сигнала на основе критерия, который может измениться от трассы к трассе (например, наклон или приращение). Двумерное преобразование Фурье представляет собой основу для анализа и реализации многоканальных процессов.
Рассмотрим шесть разрезов с нулевым выносом на рис.1-65. Расстояние между трассами равно 25м; на каждый разрез приходится 24 трассы. Все разрезы содержат монохроматические сигналы с частотой 12Гц и с наклонами, которые изменяются от 0 до 15мс на трассу. Из Раздела 1.2, где рассматривается одновременное преобразование Фурье, мы знаем, что частота – это количество циклов в единицу времени. Это двойное преобразование Фурье для функции времени. Однако, сейсмическое волновое поле – это не только функция времени, но и пространственная переменная (ось выноса или средних точек). Двойное преобразование Фурье для пространственной переменной определяется как пространственная частота, которая представляет собой количество циклов на единицу расстояния или волновое число. Так же как временная частота данной синусоиды определяется путем подсчета количества пиков в единицу времени, предположим, в 1с, волновое число наклонного сигнала определяется путем подсчета пиков в единице расстояния, например, в 1км. в горизонтальном направлении. Так же как временная частота Найквиста определяется как [1/(2 ? шаг дискретизации)], волновое число Найквиста определяется как [1/(2 ? шаг между трассами)]. Для всех разрезов на рис.1-65 – 1-70 волновое число равно 20 циклов на км, т.к. шаг между трассами равен 25м. Чтобы рассчитать волновое число, которое ассоциировано с разрезом, соответствующим наклону 15мс на трассу на рис.1-65, будем следовать пику или впадине по разрезу. Сначала рассчитаем полный временной наклон по разрезу:
(23 трассы на разрез) ? (15мс на трассу) = 345мс на разрез
Затем преобразуем результат в циклы, разделив его на период:
(345мс на разрез)/[(1000мс/разрез)/(12 циклов/с)] = 4.14 циклов/разрез
Пространственная протяженность разреза равна 575м; следовательно, волновое число, ассоциированное с этим наклоном (15мс на трассу) и с частотой 12Гц, равно:
(4.14 циклов/разрез)/(0.575км/разрез) = 7.2 циклов/км
Чтобы продолжить это обсуждение, перенесем разрез на плоскость зависимости временной частоты от пространственного волнового числа и посмотрим на два квадранта этой плоскости. Воспользуемся следующим положением: сигналам, падающим влево, присваивается положительный наклон, а сигналам, восстающим вправо, присваивается отрицательный наклон. Положительные наклоны попадают в правый квадрант, который соответствует положительным волновым числам, а отрицательные наклоны попадают в левый квадрант, который соответствует отрицательным волновым числам.
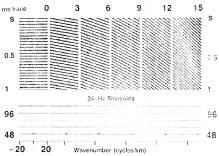 Рис.1-66 То же самое, что на рис.1-65, но используются 24-герцовые одночастотные сигналы. Рис.1-66 То же самое, что на рис.1-65, но используются 24-герцовые одночастотные сигналы.  Рис.1-67 То же самое, что на рис.1-65, но используются 36-герцовые одночастотные сигналы. Рис.1-67 То же самое, что на рис.1-65, но используются 36-герцовые одночастотные сигналы. 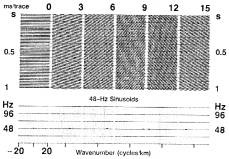 Рис.1-68 То же самое, что на рис.1-65, но используются 48-герцовые одночастотные сигналы. Рис.1-68 То же самое, что на рис.1-65, но используются 48-герцовые одночастотные сигналы. | Плоскость частот и волновых чисел (плоскость f-k) показана под каждым разрезом на рис.1-65. Разрез с горизонтальными сигналами попадает в одну точку на оси частот при 12Гц. Нулевой наклон эквивалентен нулевому волновому числу. Величина всплеска соответствует амплитуде пика синусоид, которые образуют трассы в разрезе. Следовательно, плоскость f-k в действительности представляет двумерный амплитудный спектр разреза (t, x). Эти данные преобразованы из пространственно-временной области в область частот и волновых чисел. Математически этот процесс описывается двумерным преобразованием Фурье. Между четырьмя переменными: пространство – время (t, x) и их двойным преобразованием Фурье (f,k) имеется взаимосвязь. Измерим обратную величину смещения во времени на разрезе 15 мс/трассу (рис.1-65), следуя пику, впадине или переходу через 0 от трассы к трассе. Смещение во времени определяется как угловой коэффициент dt/dx. В этом случае обратная величина смещения во времени имеет вид: dx/dt = 575 м/0.345c = 1/67км/c Сейчас рассчитаем отношение: f/k = (12 циклов/c)/(7/2 циклов/км) = 1.67км/с Отсюда обратная величина углового коэффициента dt/dx, измеренного в пространстве (t, x) вдоль постоянной фазы, равна отношению частоты к волновому числу, ассоциированному с сигналом. Следовательно, при фиксированном смещении во времени dt/dx удваивание частоты означает удваивание волнового числа. Все разрезы на рис.1-65 имеют один и тот же частотный состав; однако, в интервале 0-15мс на трассу количество |
пиков возрастает в горизонтальном направлении для каждого разреза. Для данной частоты более сильные наклоны присваиваются более высоким волновым числам, как видно на графиках f-k.
На рис.1-65 – 1-70 рассмотрим один и тот же наклон, но при разных частотах. Разместим каждый отдельный разрез на плоскости f-k. Ничего необычного не происходит, пока не дойдем до разреза с наклоном 15мс на трассу при 36Гц (рис.1-67). Здесь нет положительного наклона. В целом разрез выглядит как шахматная доска и поэтому сложно определить, является наклон положительным или отрицательным.
 Рис.1-69 То же самое, что на рис.1-65, но используются 60-герцовые одночастотные сигналы. Рис.1-69 То же самое, что на рис.1-65, но используются 60-герцовые одночастотные сигналы. 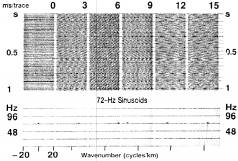 Рис.1-70 То же самое, что на рис.1-65, но используются 72-герцовые одночастотные сигналы. Рис.1-70 То же самое, что на рис.1-65, но используются 72-герцовые одночастотные сигналы. 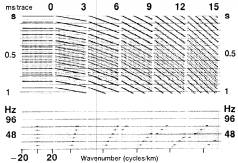 Рис.1-71 Верхний ряд: шесть выборок, каждая из которых образована путем суммирования выборок с одинаковыми наклонами на рис.1-65 – 1-70. Шаг между трассами – 25м. Нижний ряд: спектры относительных амплитуд. Рис.1-71 Верхний ряд: шесть выборок, каждая из которых образована путем суммирования выборок с одинаковыми наклонами на рис.1-65 – 1-70. Шаг между трассами – 25м. Нижний ряд: спектры относительных амплитуд. | При частоте 48Гц (рис.1-68) направление наклона можно видеть на первых четырех разрезах. Пятый разрез, который соответствует положительному наклону 12мс на трассу, показывает отрицательный наклон. Следовательно, он попадает на отрицательный квадрант – не на тот, который должен быть для этого разреза. Данный наклон (12мс на трассу) при частоте 48 Гц является пространственно неоднозначным. Фактически любой наклон больше 12мс на трассу при данной частоте является пространственно неоднозначным. В следующем наборе разрезов на рис.1-69 пространственная неоднозначность имеет место при 60Гц для наклона 9мс на трассу. Пространственная неоднозначность не только обуславливает попадание не в “свой” квадрант, но и дает неправильный наклон. Одним из примеров этого является распределение наклона 15мс на трассу при 60Гц (рис.1-69). При 72Гц (рис.1-70) наклон 6мс на трассу находится на грани пространственной неоднозначности. Наклон 15мс на трассу дважды пространственно неоднозначен: он переходит в квадрант с положительным наклоном и выглядит как меньший наклон. Этот же анализ можно использовать для отрицательных наклонов. Из рис.1-65 – 1-70 можно видеть, что каждый разрез в целом можно расположить на одной точке в области частот и волновых чисел. Каждый разрез имеет ассоциированную уникальную частоту и волновое число, присвоенные ему. Эти разрезы с нулевыми выносами можно рассматривать как представления плоских волн, которые распространяются под одним углом к вертикали и несут монохроматический сигнал. Волновой фронт определяется как линия постоянной фазы; направление распространения перпендикулярно волновому фронту. Поскольку сейсмическое волновое поле представляет собой суперпозицию большого количества наклонов и частот, оно эквивалентно синтезу нескольких плосковолновых составляющих. В этом смысле важен физический смысл |
двумерного преобразования Фурье, т.к. это способ наложения волнового поля на плосковолновые составляющие.
Зарегистрированное волновое поле представляет собой сочетание большого количества наклонов и частот таких как на рис.1-65 – 1-70. Предположим, что мы выполнили наложение разрезов с одним и тем же наклоном, но с разными частотами. Составные разрезы вместе с составными амплитудами показаны вместе с соответствующими амплитудными спектрами. Для данного наклона все частотные составляющие занимают положение не плоскости f-k вдоль прямой линии, проходящей через начало. Чем больше наклон, тем ближе радиальная линия в f-k области к оси волновых чисел. Компонента, представляющая собой нулевой наклон, располагается вдоль оси частот. По наклонам 9, 12 и 15мс на трассу видно, что пространственно неоднозначные частоты расположены вдоль линейных участков, которые переходят в противоположный квадрант в амплитудном спектре. Чем больше наклон, тем меньше частота, на которой возникает пространственная неоднозначность.
Был рассмотрен дискретный ряд частот. Для непрерывной среды частотных составляющих, ассоциированных с одним наклоном, что они будут распределяться вдоль прямой линии в области f-k. Это показано на рис.1-72. Наклонный сигнал на рис.1-73 является пространственно неоднозначным начиная приблизительно с 12Гц.
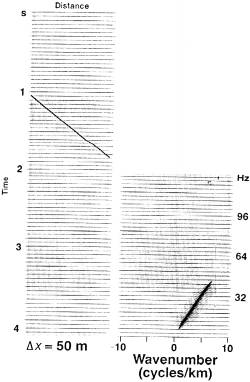 Рис.1-72 Отдельный изолированный наклонный сигнал и его двумерный амплитудный спектр. Пространственно неоднозначная частота отсутствует. Что такое наклон сигнала в мс на трассу? Рис.1-72 Отдельный изолированный наклонный сигнал и его двумерный амплитудный спектр. Пространственно неоднозначная частота отсутствует. Что такое наклон сигнала в мс на трассу? | 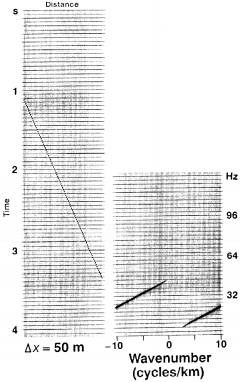 Рис.1-73 Отдельный изолированный наклонный сигнал и его двумерный амплитудный спектр. Частоты 21Гц являются пространственно неоднозначными. Рис.1-73 Отдельный изолированный наклонный сигнал и его двумерный амплитудный спектр. Частоты 21Гц являются пространственно неоднозначными. |
Исследование монохромных разрезов с одним наклоном на рис.1-65 – 1-70 показывает, что каждый разрез попадает в одну точку в области (f, k). Это наблюдение продолжено на рис.1-74. Сигналы с одним и тем же наклоном в пространстве (t, x) независимо от их положения попадают на одну радиальную линию в пространстве (f, k). Когда сигналы являются пространственно неоднозначными, радиальная линия совершает переход при волновом числе Найквиста (рис.1-75). Эти концепции имеют важное практическое значение, т.к. они ведут к пространственной f-k-фильтрации (Раздел 1.6.2). Сигналы с различными наклонами, которые могут интерферировать в области (t, x), могут быть изолированы в области (f, k).
Числовой расчет двумерного преобразования Фурье включает два одномерных преобразования Фурье. На рис.1-76 показаны шаги преобразования. Кратная математическая формулировка двумерного преобразования Фурье приводится в Приложении А.
