Двухфакторный дисперсионный анализ с однократными наблюдениями

Здесь рассматривается возможное влияние нескольких факторов на некоторую переменную 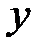. Как и в однофакторном анализе, факторы могут быть и числовыми, но и в этом случае учитывается только, сколько различных значений (уровней) принимает фактор, а не величина этих значений. Рассмотрим наиболее простую двухфакторную модель.

Изучаем влияние факторов А и В на переменную 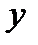. Модель можно представить в виде

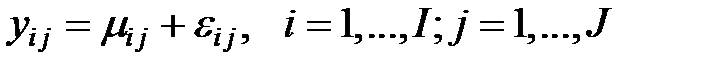, (8)
где 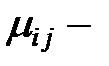некоторые константы, 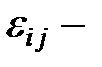случайные ошибки, 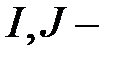число уровней факторов А и В соответственно, а 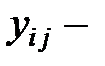наблюдение, полученное на i-м уровне фактора А и j-м уровне фактора В.

Случайные ошибки удовлетворяют тем же требованиям, что и в преды-дущем пункте.

Предположим, что между факторами нет взаимодействия. Это означает, что влияние одного фактора на величину 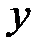не зависит от того, на каком уровне находится другой фактор. От этого допущения нельзя отказаться, так как при однократных наблюдениях слишком мало исходных данных для оценки более сложной модели. Тогда уравнение (8) можно записать в виде

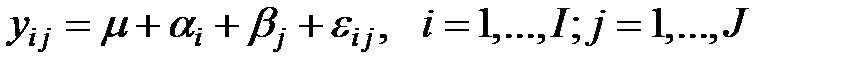. (9)

Здесь 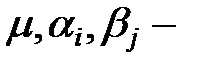некоторые константы, имеющие следующий смысл: 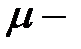общее среднее, 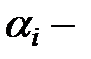эффект фактора А на его i-м уровне, 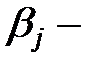эффект фактора В на его j-м уровне.

Пусть мы хотим проверить предположение о том, что фактор А или В не влияет на переменную 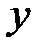. Иначе говоря, нужно проверить гипотезы о равен-стве нулю соответствующих эффектов 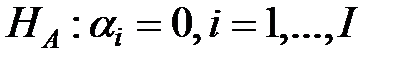и .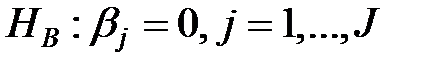

Для этого нужно вычислить следующие величины:
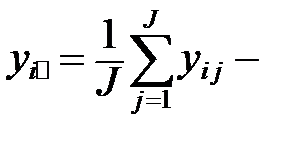средние по строкам;
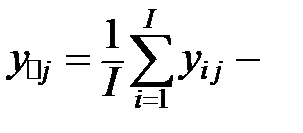средние по столбцам;
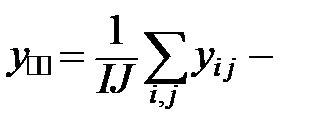общее среднее.

Эти величины вместе с исходными данными обычно записывают в таблицу 4.

Таблица 4. Исходные данные

j i			…	J	Средние по строке
			…
			…
…	…	…	…	…
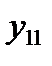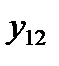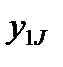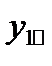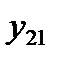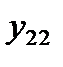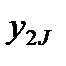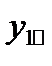I			…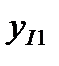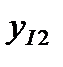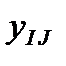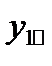
Средние по столбцу			…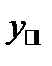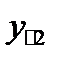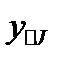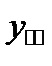

Далее вычисляем 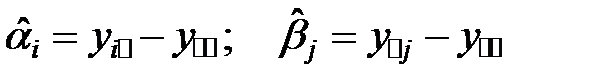. Эти величины являются несмещенными оценками соответствующих параметров 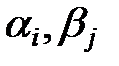модели (9). Поэтому, если гипотезы 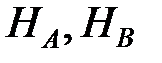верны (т.е. эффекты равны нулю), то 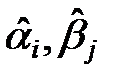не должны значимо отличаться от нуля.

Алгоритм проверки гипотез, как и в предыдущем пункте, основан на 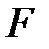- критерии и состоит в следующем. Вычисляем

а) суммы квадратов

.
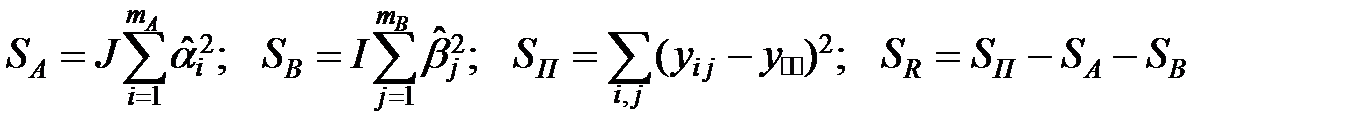Здесь 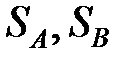характеризуют величину эффектов, 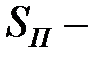полная сумма квадратов, а остаточная сумма 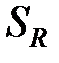служит для оценки дисперсии ошибок наблюдений при условиях а), б), в) из предыдущего пункта;

б) средние суммы квадратов:
;

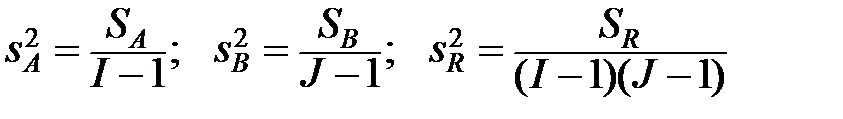в) значения 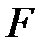- критериев для гипотез : .

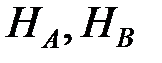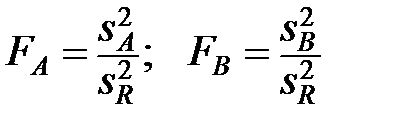Эти величины подчиняются F-распределению с числами степеней свободы, равными m_A, m_R и m_B, m_R соответственно. Здесь m_A= I– 1, m_B= J– 1 , m_R= m_Am_R.

Зададим уровень значимости α и найдем в таблице квантилей F– рас-пределения критические значения F_крит для этих степеней свободы (для каждой гипотезы свое критическое значение, причем γ = 1 - α).

Правило
Если F_A> F_крит, то гипотеза H_Aотвергается, если F_A≤ F_крит, то гипотеза принимается.
Аналогичное правило для H_B .

Результаты дисперсионного анализа обычно сводят в таблицу 5.

Таблица 5. Дисперсионный анализ

Источник изменчивости	Сумма квадратов	Степени свободы	Средняя сумма квадратов	F-отношение
фактор А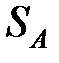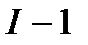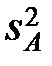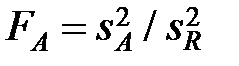

Окончание табл. 5

Источник изменчивости	Сумма квадратов	Степени свободы	Средняя сумма квадратов	F-отно-шение
фактор В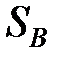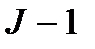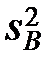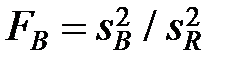
ошибка эксперимента				–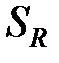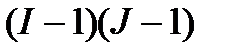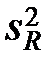
–			–	–

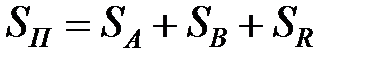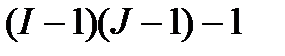Пример

Таблица 6. Исходные данные

В А					Средние по строке
	2,68	3,29	2,88	4,45	3,32
	4,12	4,96	5,09	5,22	4,85
	5,52	4,50	5,42	5,29	5,18
Средние по столбцу	4,11	4,25	4,46	4,99	4,45

Таблица 7. Дисперсионный анализ

Источник изменчивости	Сумма квадратов	Степени свободы	Средняя сумма квадратов	F-отношение
фактор А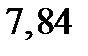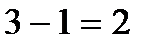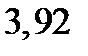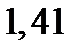
фактор В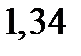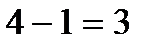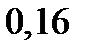
ошибка эксперимента				–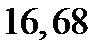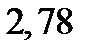
–			–	–

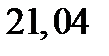Задаем уровень значимости 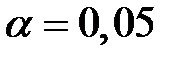и находим из таблиц 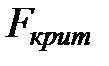для каждой из гипотез.

Для гипотезы : .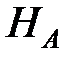

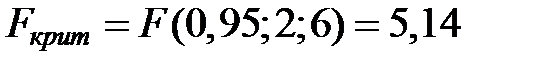Для гипотезы : .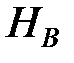

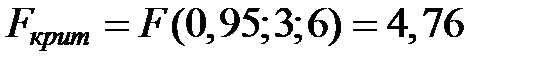Очевидно, в обоих случаях 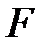- отношение меньше, чем 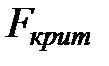(см. таблицу 7). Следовательно, на уровне значимости 0,05 экспериментальные данные не противоречат этим гипотезам. Иначе говоря, следует принять гипотезы о том, что факторы А и В не влияют на переменную .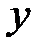