Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона 1 страница
Приняв гипотезу о нормальном распределении генеральной совокупности признака, выпишем функцию распределения плотности вероятности с учетом найденных параметров:
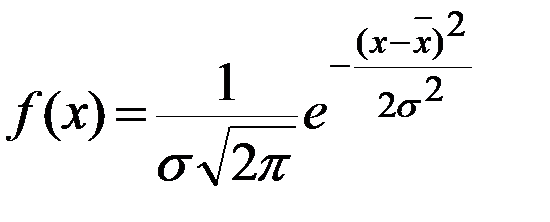или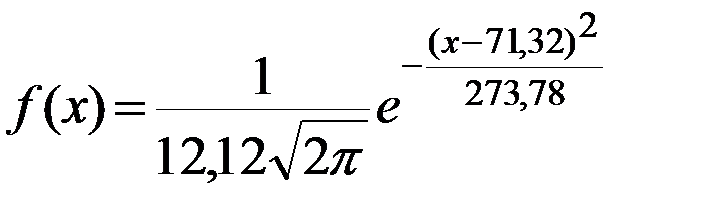 
для нашего статистического распределения.
Используя данную функцию, вычислим теоретические частоты распределения по формуле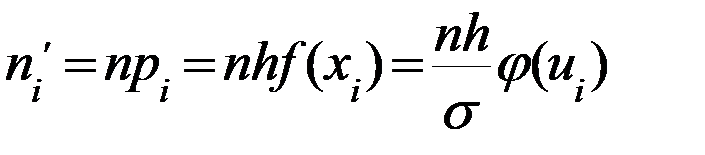 
, гдерi – вероятность попадания нормально распределенной случайной величины по найденным параметрам 
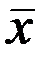и s в частичный интервал [ai; bi]: 
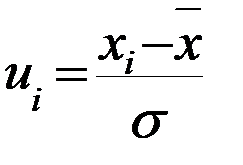– вспомогательный промежуточный параметр, 
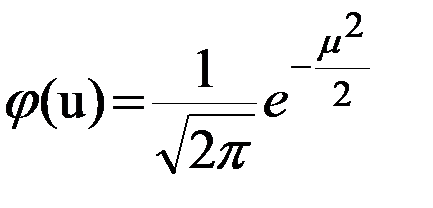– табулированная функция Гаусса,значения которой берутся по таблице (Приложение 1). В силу четности, j(– u) = j(u). Так как h = 2, вычислим значение вспомогательной величины 
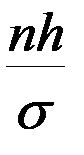. Найденные значения теоретических частот округляем до целых чисел. Все вычисления оформляются в дополнительной таблице (сделать расчеты самостоятельно).
Предварительно рекомендуется объединить между собой соседние малочисленные интервалы, суммируя их частоты, в итоге каждый интервал должен содержать не менее пяти вариантов. В рассматриваемом примере следует объединить три первых и три последних интервала. Вычисляем наблюдаемое значение критерия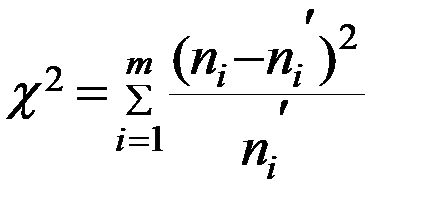
и сравниваем его с критическим (табличным).
Варианты заданий для математической статистики
Вариант 0
N=200. Начало первого интервала: 59. Длина интервала: 2.
Вариант 1
N=181. Начало первого интервала: 102. Длина интервала: 4.
Вариант 2
N=213. Начало первого интервала: 62. Длина интервала: 4.
Вариант 3
| -29 | -22 | -16 | -20 | -16 | -18 | -28 | -20 | -32 | -22 | -23 | -26 | -10 | -25 | -25 | |
| -29 | -29 | -19 | -12 | -26 | -18 | -20 | -9 | -24 | -20 | -19 | -26 | -23 | -11 | -26 | |
| -30 | -23 | -30 | -18 | -20 | -13 | -17 | -24 | -28 | -26 | -21 | -21 | -26 | -24 | -38 | |
| -23 | -24 | -25 | -20 | -23 | -17 | -11 | -22 | -19 | -19 | -25 | -29 | -23 | -16 | -25 | |
| -15 | -18 | -17 | -19 | -21 | -12 | -24 | -30 | -33 | -22 | -15 | -18 | -26 | -22 | -19 | |
| -25 | -23 | -21 | -22 | -22 | -25 | -16 | -25 | -19 | -17 | -30 | -13 | -25 | -19 | -24 | |
| -17 | -24 | -16 | -23 | -15 | -22 | -22 | -19 | -20 | -19 | -33 | -14 | -17 | -21 | -16 | |
| -24 | -13 | -20 | -19 | -17 | -13 | -27 | -25 | -25 | -19 | -22 | -22 | -22 | -23 | -9 | |
| -11 | -22 | -24 | -18 | -19 | -18 | -31 | -16 | -18 | -24 | -14 | -23 | -26 | -25 | -19 | |
| -23 | -24 | -21 | -26 | -25 | -18 | -16 | -30 | -16 | -24 | -13 | -14 | -18 | -22 | -22 | |
| -28 | -18 | -21 | -31 | -23 | -23 | -27 | -21 | -21 | -22 | -34 | -24 | -20 | -24 | ||
| -21 | -32 | -16 | -18 | -15 | -22 | -15 | -22 | -18 | |||||||
N=175. Начало первого интервала: -37. Длина интервала: 2.
Вариант 4
N=194. Начало первого интервала: 39. Длина интервала: 6.
Вариант 5
| -14 | -1 | -4 | -17 | -22 | |||||||||||
| -9 | -8 | -5 | |||||||||||||
| -21 | -20 | -17 | -21 | -2 | |||||||||||
| -6 | -2 | -1 | |||||||||||||
| -8 | -13 | ||||||||||||||
| -1 | -10 | -7 | -5 | -2 | -10 | ||||||||||
| -5 | -12 | -2 | -20 | -4 | -2 | ||||||||||
| -11 | -7 | -20 | -2 | -12 | -3 | -7 | -9 | ||||||||
| -8 | -12 | -22 | -9 | -7 | |||||||||||
| -10 | -8 | ||||||||||||||
| -16 | -8 | -1 | -5 | -5 | |||||||||||
| -2 | -6 | -2 | |||||||||||||
| -16 | -22 | -7 | -4 | -9 | |||||||||||
| -16 | -9 | -8 | -2 | ||||||||||||
| -7 | -14 | -5 | |||||||||||||
| -2 | |||||||||||||||
N=229. Начало первого интервала: -25. Длина интервала: 6.
Вариант 6
N=237. Начало первого интервала: 285. Длина интервала: 7.
Вариант 8
N=235. Начало первого интервала: 28. Длина интервала: 5.
Вариант 9
N=217. Начало первого интервала: 26. Длина интервала: 5.