Аппроксимация функций методом наименьших квадратов

Основным недостатком интерполяционных многочленов является наличие у них большого числа экстремумов и точек перегибов, что определяется суммированием в них многочленов 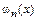, n раз меняющих свой знак. Кроме того, исходные табличные значения функции заданы неточно по разным причинам, поэтому строить многочлены выше 4-5-й степени, зная, что из теоретических исследований функция в интервале таблицы совсем не такая, не имеет особого смысла.

Если табличные значения функции можно интерпретировать как теоретическое значение плюс погрешность, то, задав некоторый критерий близости теоретической кривой к заданному множеству табличных точек, можно найти нужное число параметров этой кривой.

Наиболее популярным критерием близости является минимум среднего квадрата отклонения:

,

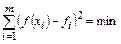где 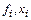– точка экспериментальных данных из таблицы,

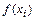– значение искомой зависимости в точке .

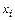Если искомую зависимость желательно представить многочленом степени n, то (n+1) коэффициент в нем будут представлять неизвестные параметры. Подставив в сумму квадратов отклонений искомый многочлен, получим функционал, зависящий от этих параметров:

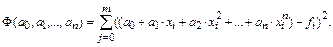
Чтобы функционал 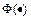был минимален, необходимо все частные производные функционала по параметрам приравнять нулю и систему разрешить относительно неизвестных параметров 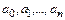. Эти действия приводят к следующей системе линейных уравнений

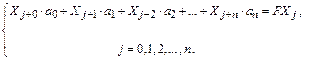
Здесь 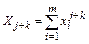– постоянный коэффициент, равный сумме (j+k)-тых степеней всех значений аргументов. Для их ручного вычисления удобно к исходной таблице данных добавить еще 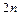столбцов. 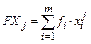– числовые значения в правой части системы линейных алгебраических уравнений, для подсчета которых тоже

удобно к исходной таблице данных добавить еще n столбцов.

Демонстрацию метода наименьших квадратов проведем для данных с количеством точек в таблице, равным 4. Максимальная степень аппроксимирующего многочлена для такого набора равна 3, так как должно выполняться соотношение: 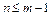. Для максимальной степени аппроксимирующий и интерполяционный многочлены равны.

Пусть таблица данных после добавления в нее дополнительных колонок выглядит следующим образом:

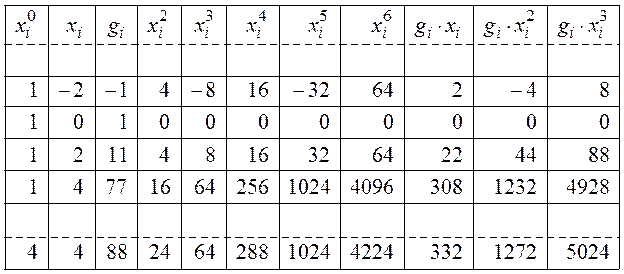
В нижней строке размещаем итоговые суммы по каждой колонке.

Система уравнений для полинома третьей степени:

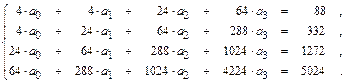
Решив систему, найдем: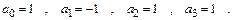

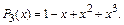
Эта же таблица без добавления чего-либо позволяет найти коэффициенты аппроксимирующего многочлена второй степени. Для этого достаточно в системе для полинома третьей степени убрать 4-е уравнение, а из остальных уравнений исключить слагаемые с неизвестной 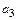. В результате система уравнений для полинома второй степени будет:

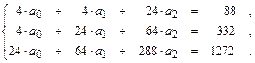
Решив систему, найдем: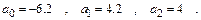

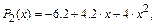
Аналогично можно уменьшать число уравнений для построения аппроксимирующих многочленов первой и нулевой степеней.

На рисунке 1 показаны графики двух аппроксимирующих многочленов второй и третьей степени. Многочлен третьей степени проходит через 4 заданные точки, а многочлен второй степени проходит сквозь множество заданных точек с минимумом суммы квадратов отклонений от них, что хорошо видно на графиках.

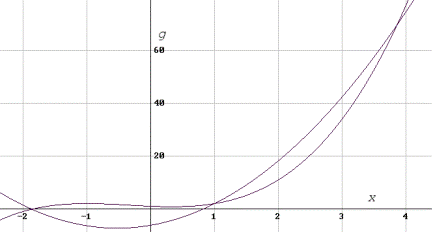
Рисунок 1.

Заключение

В вычислительной математике существенную роль играет интерполяция функций, т.е. построение по заданной функции другой (как правило, более простой), значения которой совпадают со значениями заданной функции в некотором числе точек. Причем интерполяция имеет как практическое, так и теоретическое значение. На практике часто возникает задача о восстановлении непрерывной функции по ее табличным значениям, например полученным в ходе некоторого эксперимента. Для вычисления многих функций оказывается эффективно приблизить их полиномами или дробно-рациональными функциями. Теория интерполирования используется при построении и исследовании квадратурных формул для численного интегрирования, для получения методов решения дифференциальных и интегральных уравнений.

Литература

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: Учеб. пособие. – М.: Наука, 1987. – 600 с.

2. Воеводин В.В. Численные методы алгебры. Теория и алгорифмы. - М.: Наука, 1966. – 248 с.

3. Воеводин В.В. Вычислительные основы линейной алгебры. – М.: Наука, 1977. – 304 с.

4. Волков Е.А. Численные методы. – М.: Наука, 1987. – 248 с.

5. Калашников В. И. Аналоговые и гибридные вычислительные устройства: Учеб. пособие. – Харьков: НТУ “ХПИ”, 2002. – 196 с.

6. Вержбицкий, В. М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Высш.шк., 2001. 383 с.

7. Волков, Е. А. Численные методы. СПб.: Лань, 2004. 248 с.

8. Мудров, А. Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. Томск: МП "РАСКО", 1991. 272 с.

9. Шуп, Т. Е. Прикладные численные методы в физике и технике. М.: Высш. шк., 1990. 255 с.

10. Бахвалов, Н. С. Численные методы в задачах и упражнениях / Н. С. Бахвалов, А. В. Лапин, Е. В. Чижонков. М.: Высш. шк., 2000. 192 с.

11. Лит.: Монографии. Ахиезер Н. И., Лекции по теории аппроксимации, 2 изд., М., 1965; Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954; Натансон И. П., Конструктивная теория функций, М. — Л., 1949; Никольский С. М., Приближение функций многих переменных и теоремы вложения, М., 1969; Тиман А. Ф., Теория приближения функций действительного переменного, М., 1960.

12. Обзоры. Математика в СССР за тридцать лет. 1917—1947, М. — Л., 1948, с. 288—318; Математика в СССР за сорок лет. 1917—1957, т. 1, М., 1959, с. 295—379; История отечественной математики, т. 3, К., 1968, с. 568—588.

С. А. Теляковский.